Euklidovská geometria

Vysvetľujeme, čo je euklidovská geometria, jej história, prvky a uvádzame niekoľko príkladov

Euclid z Alexandrie a jej prvky, od Jusepe de Ribera, vedľa, dve neparalelné čiary a čiara, ktorá ich prerezáva, ilustrujúce piaty postulat. Zdroj: Wikimedia Commons.

Čo je euklidovská geometria?

Ten Euklidovská geometria Je to ten, ktorý riadi tieto postuláty Euclid de Alejandría, grécky geometer, ktorý žil smerom k 300.C, na ktorom česť je táto disciplína pomenovaná, pretože bola prvá, ktorá ju systematizovala.

Táto vetva matematiky študuje vlastnosti línií, rovín, uhlov a geometrických čísel, ako sú polygóny, obvody a iné kužeľ. Preto je dôležitý vo vede a inžinierstve, ktorého vývoj výrazne vyvolal.

Na druhej strane bola euklidovská geometria prvou presnou vedou, pretože s ňou začala cesta systematizácie vedy, ako aj použitie logiky na demonštráciu z niekoľkých axiómov, početných návrhov nazývaných teorémy, s cieľom opísať vlastnosti geometrických objektov.

História

Geometria má dlhú históriu, pretože záujem ľudstva v nej je veľmi stará a centrálna os euklidovskej geometrie je práca Predmety, múdreho euklidu z Alexandrie, mesta nachádzajúceho sa v Egypte a ktoré žilo vo štvrtom storočí.C.

V tom čase boli známe najdôležitejšie vlastnosti mnohých čísel a geometrických telies. Existovali rozsiahle vedomosti o geometrii, ale všetko bolo empirické a chýbalo mu systematizácia.

Potom egyptský kráľ Ptolemy a poveril už slávneho euklidového učiteľa, ktorého škola bola v Alexandrii, aby zorganizovala všetky dostupné matematické a geometrické znalosti, vrátane vetiech a vlastností.

Euclides začal pracovať a vedľa svojich učeníkov napísal svoje pracovné prvky, ktoré rozdelil do trinástich kníh ako kapitoly. Táto práca by sa stala referenciou pre geometriu pre budúce generácie.

Môže vám slúžiť: následné deriváty

Prvky euklidov

Obsah prvkov je usporiadaný nasledovne:

• V knihách I až IV Flat Geometria sa vyvíja.
• V knihách V a ja som videl teóriu proporcie.
• Knihy IX sú venované aritmetike.
• V knihe X sa objaví neschopnosť,
• Geometria priestoru v knihách XI až XIII.

Euklidovská geometria bola základom mnohých zadných geometrických vývojov av súčasnosti sa vyučuje vo všetkých školách na svete.

Má tiež nactu, že je prvou prácou, ktorá zahŕňa starostlivé demonštrácie založené na logickom zdôvodnení a tiež pri poskytovaní koherencie tela geometrických a matematických znalostí tej doby.

Základné prvky euklidovskej geometrie

Euklidovská geometria je postavená okolo štyroch základných prvkov opísaných v knihe I prvkov:

1. Nafúknuť
2. Priamy
3. Plochý
4. Priestor

1. Nafúknuť

A nafúknuť Chýba mu rozmery alebo časti a odlišuje sa od iného bodu jednoducho podľa jeho umiestnenia. Ak sú dva body A a B rôzne, je to preto, že majú rôzne polohy, ktoré sú označené dobre známymi karteziánskymi súradnicami (x, y), ak je bod v rovine alebo súradnice (x, y, z) Ak je vo vesmíre.

Je pozoruhodné, že karteziánsky systém nie je súčasťou Predmety euklid, ale objavil sa oveľa neskôr v 1600 rokoch a je to kvôli René Descartes.

2. Priamy

Ten priamy Je to nekonečná zbierka bodov a má iba dĺžku, nie šírku. Časť sa zvyčajne nakreslí, pričom šípky zdôrazňujú, že čiara pokračuje neurčito.

3. Plochý

A plochý Je to neobmedzený povrch, takže má dve rozmery, z ktorých je časť zastúpená, pomocou štvorca alebo obdĺžnika.

Tam v lietadle je okrem iného veľa geometrických čísel, ako sú čiary, otvorené a zatvorené krivky a polygóny.

Môže vám slúžiť: Všeobecná rovnica riadku, ktorej sklon sa rovná 2/3

4. Priestor

Nakoniec existuje priestor So svojimi tromi rozmermi, schopnými umiestňovať všetky body. Obsahuje roviny a geometrické telá charakterizované ich objemom, ako je polyhedra, gule a ďalšie.

Môžu sa považovať za základné definície euklidovskej geometrie, ale okrem nich Euclides ponúka vo svojej práci asi 150 rozmanitých definícií.

Bežné predstavy

Pozostávajú zo zrejmých a intuitívnych skutočností, ktoré nepatria správne k rozsahu geometrie a používajú sa ako rozvíjajúce sa koncepty. Vzťahujú sa na „veci“ vo veľmi širokom kontexte:

1. Veci rovnaké ako niečo iné, sú navzájom rovnaké.
2. Ak sa veci pridávajú do inej sady vecí a všetky sú rovnaké, aké výsledky sú tiež rovnaké.
3. Ak sú ukradnuté rovnaké veci, zostávajúci je tiež rovnaký.
4. Keď sa veci zhodujú medzi sebou, je to preto, že sú rovnaké.
5. Celý je vždy väčší ako strany, odobraté osobitne.

Postuláty euklidovskej geometrie

Postuláty alebo axiómy sú jednoduché vyhlásenia, ktoré sa považujú za skutočné a zrejmé, takže nevyžadujú demonštráciu.

Predstavujú základ euklidovskej a euklidovej geometrie, ktorá zakladá päť v ich knihe I:

1. Buďte dvoma rôznymi bodmi a B, prechádza cez ne iba jeden riadok, to znamená, že dva body určujú čiaru.
2. Akýkoľvek priamy segment sa dá predĺžiť na neurčito, aby predstavoval čiaru, a preto každý segment patrí do riadku.
3. Ak máte dva rôzne body alebo a, môžete vždy nakresliť kruh so stredom O a polomerom rovným segmentom OA.
4. Všetky priame uhly sú medzi sebou zhodné.
5. Vzhľadom na čiaru a bod P, ktorý k nej nepatrí, je to vždy možné.

Posledný postulát, najmä v pôvodnej verzii, nevyzerá tak jednoduché ako ostatné. Uvádza sa v tom:

Môže vám slúžiť: Heptagon

„Ak priama čiara, ktorá padá na ďalšie dve čiary, robí dva vnútorné uhly na tej istej strane menej ako dva priame uhly, povedali priame čiary, rozšírené neurčito, sú (pretína) na strane, na ktorej sú menšie uhly, že sú také dva priame uhly “.

To znamená, že pôvodne predpokladá 5, stanovuje podmienku tak, aby dve riadky neboli rovnobežné. Ale je jasnejšie, keď je napísané takým spôsobom, že ilustruje opak, to znamená paralelizmus riadkov.

Príklady euklidovskej geometrie

Príklad 1

Existujú tri rôzne body označené písmenami A, B a C.

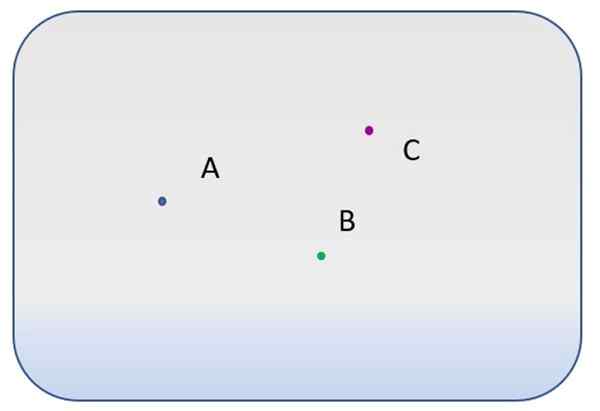
1. Koľko rôznych riadkov prechádza bodom a?
2. A koľko je možné nakresliť medzi bodmi A a B? A medzi A a C?
3. Je možné nakresliť čiaru, na ktoré body A, B a C?

Odpovedať

Podľa postulátu i, nekonečné priame čiary môžu byť pretiahnuté cez A, pretože na určenie čiary sú potrebné dva body.

Odpoveď B

Entre A a B je možné nakresliť iba čiaru. A tiež medzi A a C.

Odpoveď c

Nie je možné, aby riadok obsahoval zároveň A, B a C.

Príklad 2

Žiada sa o vytvorenie krok za krokom rovnostranný trojuholník (všetky jeho strany sú rovnaké), pozná jednu zo svojich strán, čo je segment AB a v každom kroku označuje postul alebo spoločnú predstavu použitú pri konštrukcii v konštrukcii v.

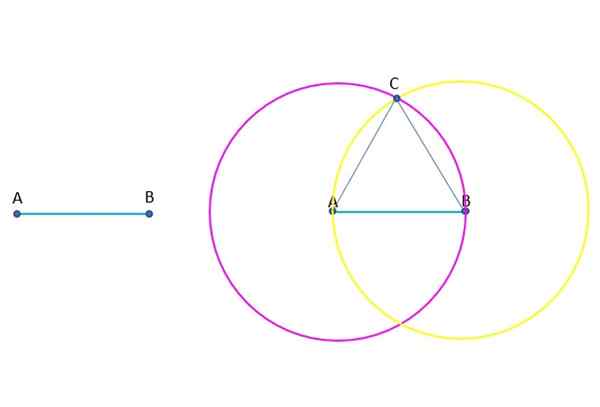Výstavba rovnostranného trojuholníka ABC. Zdroj: f. Zapata.

Odpoveď

Krok 1

Kruh so stredom v A a Rádiu AB je nakreslený. To je vždy možné, podľa postulátu III.

Krok 2

Nakreslený je ďalší obvod so stredom v B a Rádiu.

Krok 3

Obe obvody, ktoré majú rovnaký polomer, sú rezané v bode C. Teraz môžete nakresliť segmenty, ktoré sa spájajú s C s a a b podľa postulátu i.

Tieto segmenty sú rádiá obvodu, a preto sú miery AC a BC rovnaké ako v prípade AB, podľa spoločného pojmu 1. Potom je trojuholník ABC rovnice.