Analytická geometria

Vysvetľujeme, aká analytická geometria, jej história, aké štúdie a aplikácie sú

Čo je analytická geometria?

Ten analytická geometria Je to odvetvie matematiky, v ktorej sa kombinujú geometria a algebra, aby sa vyriešili rôzne geometrické problémy prostredníctvom algebraických techník.

Používajte koordinačné systémy, ako napríklad karteziánsky súradnicový systém, ktorý dlhuje svoj názov René Descartes. Týmto spôsobom je možné priradiť krivky v rovine a vo vesmíre s algebraickými rovnicami.

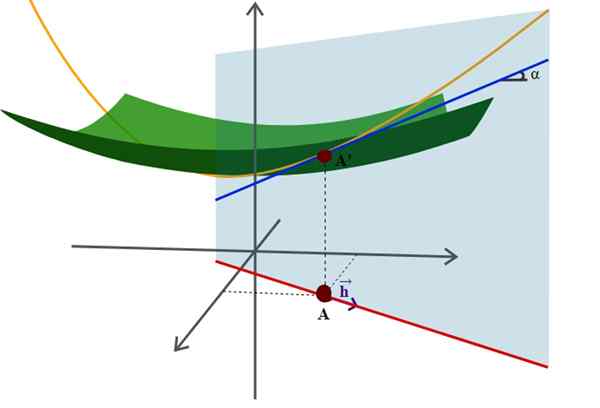
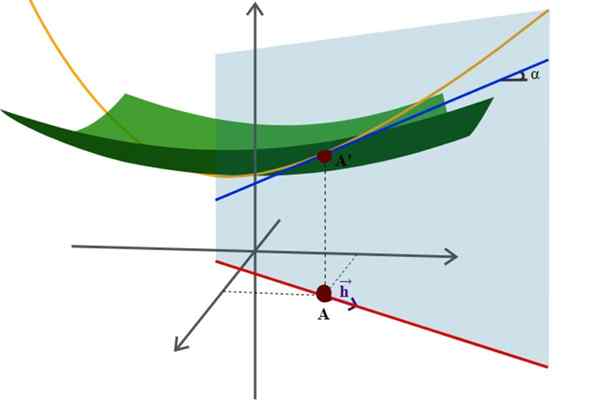Schéma povrchu vo vesmíre a jeho smerovom deriváte, jednej z mnohých pokročilejších aplikácií analytickej geometrie. Zdroj: Wikimedia Commons.

Príkladom je dobre známa rovnica polomeru R -Riortion zameraná na pôvod súradnicového systému:

V mnohých prípadoch je nepochybne jednoduchšie pracovať s algebraickým vyjadrením krivky, ako s jej geometrickým znázornením samotným. To je prípad pri výpočte priesečníkov medzi krivkami alebo nájdením dotykových alebo sušených čiar.

Podobne prostredníctvom analytickej geometrie je možné rozložiť funkcie grafiky. A ako je známe, funkcie umožňujú modelovanie vedeckých a inžinierskych problémov. Preto je analytická geometria prítomná v učebných osnovách kariéry spojených s týmito oblasťami vedomostí.

Stručná história analytickej geometrie

Analytická geometria má svoj pôvod v prvej polovici 17. storočia rukou dvoch významných francúzskych matematikov: René Descartes (1596-1650) a Pierre de Fermat (1601-1665).

Rene Descartes

Dá sa však povedať, že jeho pozadie sa darí storočiam, gréckym matematikom Apollonius z Pergamo (262-190 a.C.). Napísal pojednanie o kužeľoch, ku ktorým udelil ich mená: obvod, elipse, podobenstvo a hyperbola.

Môže vám slúžiť: Zložená proporcionalita: Vysvetlenie, tri zložené pravidlo, cvičenia

Práca Apollonia bola teda základom pre, oveľa neskôr, francúzsky René Descartes a Pierre de Fermat položili základy analytickej geometrie nezávisle. Ale Descartes je považovaný za otca tejto vedy, pretože bol prvým, kto zverejnil svoje diela.

Descartes, Fermat a Euler

V reči metódy z roku 1637 Descartes zjednotil dve disciplíny, ktoré boli dovtedy oddelené: algebra a geometria. Descartes vo svojej práci predstavuje karteziánsky súradnicový systém, aby lokalizoval body v lietadle a vo vesmíre.

Využíva tiež druhé algebraické rovnice s dvoma premennými, na opis kónických sekcií a je venovaný riešeniu geometrických problémov s nimi. Vytvoriť tiež dobrú časť matematického zápisu, ktorý sa v súčasnosti používa.

Pierre de Fermat je viac spojený s optikou ako s analytickou geometriou, ich príspevky sú však pozoruhodné.

V roku 1629 Fermat obnovil kužeľ Apollonius z Pergamo a vytvoril techniky, ktoré tvoria analytickú geometriu, vymyslí svoj vlastný súradnicový systém a jasne definuje kľúčový koncept koncepcie Geometrické miesto, s ktorými sa začína štúdium analytickej geometrie.

Fermatove diela však nevideli svetlo až do roku 1679, publikované jeho syn, keď matematik už zomrel. Z tohto dôvodu sa otcovstvo analytickej geometrie pripisuje Descartes.

Následne k francúzskym matematikom založil švajčiarsky Leonardo Euler (1707-1783) formálne základy analytickej geometrie. Euler zaviedol v rovine a priestore niekoľko súradnicových systémov: obdĺžnikové, polárne a šikmé súradnice, ako aj transformácie z jedného systému do druhého.

Môže vám slúžiť: Ako sa informácie získajú v prieskume?

Vo svojich dielach o analytickej geometrii Euler tiež prehĺbil klasifikáciu rôznych kriviek, podľa stupňa reprezentatívnej algebraickej rovnice (tretí a štvrtý poriadok) a intenzívne študoval jej vlastnosti, rovnice tangentov, zakrivenia, symetrie a veľa viac.

Aké štúdie analytická geometria?

Všeobecne povedané, analytická geometria sa zameriava na štúdium geometrických prvkov, ako sú body, segmenty, čiary, krivky, povrchy a zväzky. Ako je uvedené vyššie, vytvára algebraické rovnice, ktoré opisujú a súvisia s týmito prvkami, čo umožňuje ich riadenie prostredníctvom algebraických techník.

Hlavné ciele analytickej geometrie veľmi súhrnným spôsobom sú nasledujúce:

1. Zriadiť karteziánsky súradnicový systém a systém polárnych súradníc, aby ste našli body v rovine, ako aj jeho rozšírenie na body vo vesmíre.
2. Nakreslite segmenty, rovné, krivky a povrchy na karteziánskej rovine a priestore.
3. Vypočítajte rovnice, ktoré analyticky opisujú krivku a jej konštrukciu v lietadle a/alebo priestore, ako aj štúdium všetkých jeho vlastností.
4. Klasifikovať krivky, povrchy a zväzky.
5. Odvodiť základné vzorce na riešenie problémov v pozoruhodných bodoch, rovných, plánoch, uhloch, paralelizme, kolmej úrovni, vzdialenosti, križovatkách, oblastiach a ďalších.
6. Vyriešte geometrické problémy pomocou aplikácie algebraických metód, pre ktoré vzorce odkazujú na pozoruhodné body, rovnice pre čiaru, plány, uhly, vzdialenosť medzi bodmi, medzi čiarami a bodmi, bodmi tangencie, suchým líniám, oblastiam, oblastiam a oveľa viac.
7. Pracujte s vektorovými priestormi a výrobkami medzi vektormi.

Vzdialenosť medzi dvoma bodmi

Ako príklad početných aplikácií analytickej geometrie je jednou z najjednoduchších výpočtu vzdialenosti medzi dvoma bodmi roviny. Sú dva body p₁ A p₂, súradníc (x₁,a₁) a (x₂,a₂) Vzdialenosť d medzi nimi sa vypočíta podľa:

Môže vám slúžiť: trinomial

Polárne súradnice

Pláne bod môže byť špecifikovaný cez svoju „R“ vzdialenosť od pôvodu súradníckeho systému, nazývaný Polo a uhol, ktorý tvorí čiaru, ktorá obsahuje bod a tyč, s horizontálnou osou alebo polárnou osou.

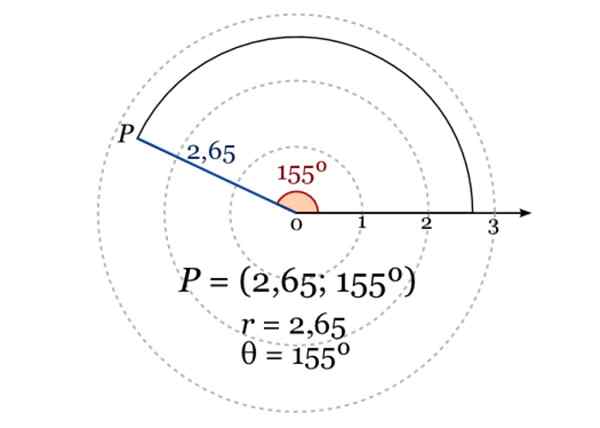Obrázok zobrazuje polárne súradnice bodu P, kde r = 2.65 a uhol v stupňoch vzhľadom na polárnu os je 155 °. Zdroj: Wikimedia Commons.

Aplikácie analytickej geometrie

Základ nekonečného výpočtu

Analytická geometria je nevyhnutná pre vývoj nekonečného výpočtu, pretože uľahčuje grafickú reprezentáciu kriviek a funkcií a analyticky s nimi spolupracuje na vytváraní modelov, ktoré predstavujú javy prírody.

Mapy

Karteziánsky súradnicový systém pomáha vytvárať mapy a identifikovať miesta prostredníctvom zemepisnej šírky a dĺžky, čo zodpovedá karteziánskym súradniciam bodu v lietadle.

Topografické výpočty

Rôzne typy súradnicových systémov sa používajú v topografii a tvoria základ ich štúdia a aplikácií. Medzi nimi je polárny súradnicový systém opísaný vyššie.

Trajektórie nebeských telies

Kuchárske rezy, opísané prostredníctvom analytickej geometrie, sa podieľajú na dôležitých javoch prírody, ako sú trajektórie nebeských telies, podlieha gravitácii sily. Napríklad planéty a niektoré kométy opisujú eliptické trajektórie okolo slnka, pričom sa nachádzajú v jednom z bodov.

Občianska architektúra

Početné krivky sú súčasťou architektonických konštrukcií, napríklad káble závesného mosta môžu mať podobu podobenstiev.

Globálne polohovacie systémy

Globálny polohovací systém alebo GPS umožňujú možné miesta s presnosťou, ako aj pohybujúce sa objekty, ako sú vozidlá a lode. Pomáha tiež ľuďom ľahšie sa dostať do ich cieľov a viesť ich na najlepších trasách.