Základné trigonometrické funkcie, v karteziánskej rovine, príklady, cvičenie

Ten trigonometrické funkcie Skutočnej premennej zodpovedajú akémukoľvek uhlu (vyjadreného v radiánoch), trigonometrickým dôvodom, ktorým môže byť sínus, kosínus, dotyčnica, cotangent, secant a Harvester.

Týmto spôsobom máme šesť trigonometrických funkcií: sínus, kosínus, tangent, kombajn, sušenie a kotangent.

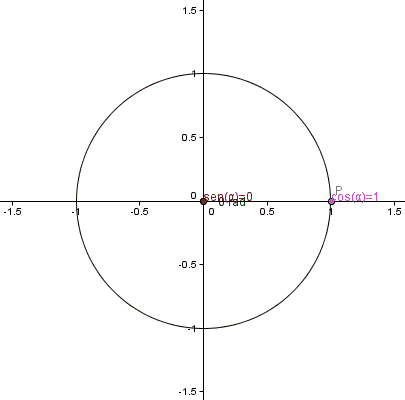postava 1. Animácia trigonometrických kruhov. Zdroj: Wikimedia Commons.

Trigonometrické funkcie pre uhly medzi 0 a 2π sú definované pomocou jednotného obvodu, rádio 1 a ktorého centrum sa zhoduje s pôvodom pôvodu karteziánskeho súradnice: bod (0,0).

Na tomto obvode môžeme nájsť akýkoľvek bod P súradníc (x, y).

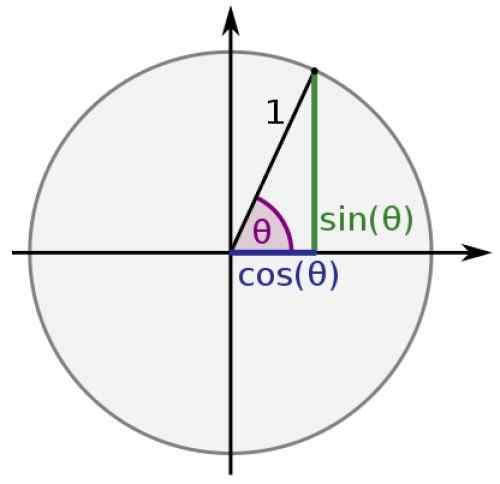
Segment, ktorý spája pôvod s P, spolu s príslušnými segmentmi, ktoré spájajú projekcie P na súradnicových osiach, tvoria obdĺžnikový trojuholník, ktorého trigonometrické dôvody sú známe ako kvocienty medzi bokmi trojuholníka. Tak:

• sin 9 = oproti /hypotenusa kateto
• cos θ = susedný /hypotenusa kateto
• TG 9 = opačný kateto /susedný kateto

A teraz dôvody, ktoré sú inverzné z vyššie uvedeného:

• sec 9 = hypotenus /susedný kateto
• Poškodenie 9 = hypotenusa /kateto oproti
• CTG 9 = susedný kateto /opačný kateto

V jednotnom kruhu sa hypotenus akéhokoľvek trojuholníka rovná 1 a kategórie majú hodnotu x a y, potom:

hriech θ = y

cos θ = x

Obrázok 2. Pravý trojuholník v jednotkovom kruhu. Zdroj: Wikimedia Commons.

Týmto spôsobom funkcie sínusov a kosínutia vždy získavajú hodnoty medzi -1 a 1, zatiaľ čo zostávajúce:

tg θ = y/x

poškodenie 9 = 1/y

Sec θ = 1/x

Nie sú definované, keď X ani a Majú hodnotu 0.

[TOC]

Trigonometrické funkcie v karteziánskej rovine

Ako uvidíme nižšie, trigonometrické funkcie sa vyznačujú periodickými. Preto nie sú bijektované, s výnimkou obmedzenej domény.

Funkcia f (x) = sin x

Začínajúc v trigonometrickom kruhu v bode P (1,0), uhol je 0 Radians. Potom sa polomer otáča v anti -horskom zmysle a funkcia Sen X postupne rastie, až kým nedosiahne π/2 radiány (90 °), čo zodpovedá 1.Približne 571 radiánov.

Môže vám slúžiť: doplnkové uhly: čo sú, výpočet, príklady, cvičenia

Tam dosahuje hodnotu y = 1 a potom klesá, až kým nedosiahne nulu v π radianoch (180 °). Následne sa to ešte viac znižuje, pretože hodnota sa stáva zápornou až do dosiahnutia −1, keď je uhol 3π/2 radiány (270 °).

Nakoniec sa znova zvyšuje, až kým sa nevráti na nulu v 360 °, kde sa všetko začína znova. To robí y = hriech x a periodická funkcia obdobia 2π, takže funkcia sínusu nie je bijective.

Okrem toho je graf symetrický vzhľadom na bod (0,0), preto je funkcia nepárna.

Potom graf y = sen x:

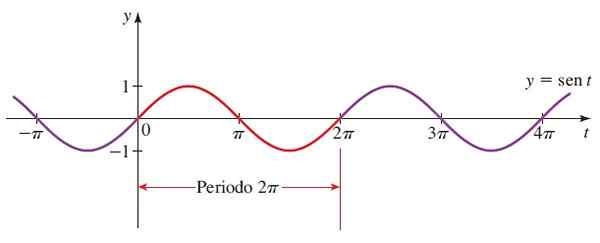Obrázok 3. Funkčný graf f (x) = sin x. Zdroj: Stewart, J. Predbežné precudzenie: matematika pre univerzitu.

Červená časť je prvá perióda. Zohľadňujú sa aj negatívne uhly, pretože polomer trigonometrického kruhu sa môže otáčať v pláne.

Doména Sen X = Všetky realy.

Sen X rozsah alebo trasa = [-1,1]

Funkcia f (x) = cos x

V bode P (1,0) Funkcia coseno má hodnotu 1 a odtiaľ klesá, keď je uhol π/2 dosiahne 0. Pokračujte v znižovaní a berie záporné hodnoty, až kým nedosiahnete -1 v uhle π.

Potom sa začne postupne zvyšovať, až kým nedosiahne 0 v 3π/2 a znova sa berie hodnota, keď polomer otočil úplné otočenie. Odtiaľ sa cyklus opakuje, pretože cos x je periodický a je tiež krútiacim momentom (symetrický okolo vertikálnej osi).

Forma funkcie kosínutia je rovnaká ako forma sínusovej funkcie, pokiaľ nie sú posunuté π/2 jedna z hľadiska druhého.

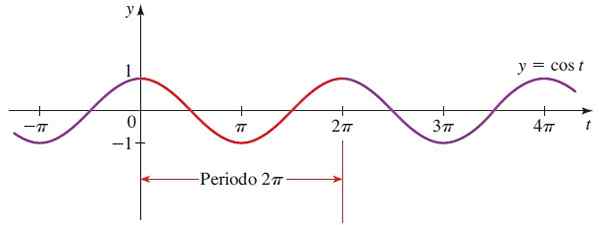Obrázok 4. Funkčný graf f (x) = sin x. Zdroj: Stewart, J. Predbežné precudzenie: matematika pre univerzitu.

Cos x doména = Všetky realy.

Môže vám slúžiť: Prebužný odhad

Rozsah alebo cos x trasa = [-1,1]

Diskontinuálne trigonometrické funkcie

Funkcie TG X, CTG X, Sec X a Hars. Pretože tieto hodnotia 0 v niektorých uhloch, keď sa objavia v menovateľovi, robia funkciu diskontinuálnu.

A keďže sínus a kosínus sú periodické funkcie, funkcie Tg x, ctg x, sec x, Harm x sú tiež.

Tangentová funkcia f (x) = tg x

Pre dotyčničnú funkciu sú hodnoty diskontinuity: ± π/2, ± 3π/2, ± 5π/2 ... tam funkcia trvá veľmi veľké alebo veľmi malé hodnoty. Všeobecne sa to stáva pre všetky násobky π formy (2n+1) π/2, kladné aj negatívne, s n = 0, 1, 2 ..

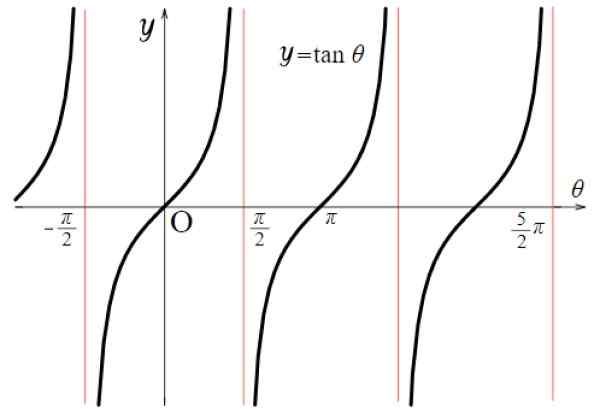Obrázok 5. Funkčný graf f (x) = tg x. Zdroj: Wikimedia Commons.

Preto:

Doména TG X: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Rank alebo TG X Tour: Všetky realles.

Všimnite si, že funkcia f (x) = tg x sa opakuje medzi - π/2 a + π/2, preto je jej perióda π. Okrem toho je to symetrické vzhľadom na pôvod.

COTANGENT FUNKCIA F (X) = CTG X

Pre túto funkciu sa hodnoty diskontinuity vyskytujú v 0, ± π, ± 2π…, to znamená celé násobky π.

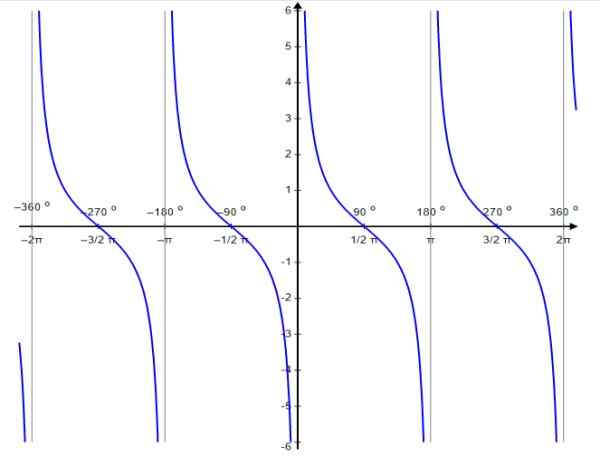Obrázok 6. Funkcia graf f (x) = cotg x. Zdroj: Wikimedia Commons.

Rovnako ako dotyčnica, aj Cotangent Function je periodická perióda π. Pre ňu je splnené, že:

Doména CTG X: D = x ∈ R / x ≠ n π; n ∈ Z

Rozsah alebo trasa CTG X: Všetky realles.

Suchovacia funkcia f (x) = sec x

Funkcia Sec X má body diskontinuity v ± π/2, ± 3π/2, ± 5π/2…, kde cos x = 0. Je to tiež periodické obdobie π a tiež sa pozoruje v grafe, že funkcia nikdy neberie hodnoty v intervale (-1,1)

Môže vám slúžiť: celé čísla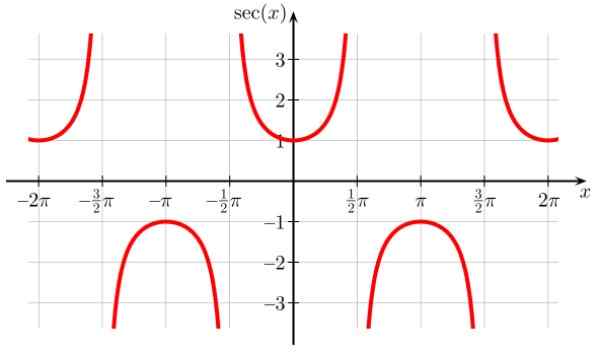 Obrázok 7. Funkčný graf f (x) = sec x. Zdroj: Wikimedia Commons.

Doma of Sec x: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Rozsah X alebo trasa: Všetky reais okrem (-1,1)

Funkcia úrody f (x) = poškodenie x

Je to podobné ako funkcia sušenia, aj keď je posunutá doprava, preto sú body diskontinuity 0, ± π, ± 2π a všetky celé násobky π. Je to tiež pravidelné.

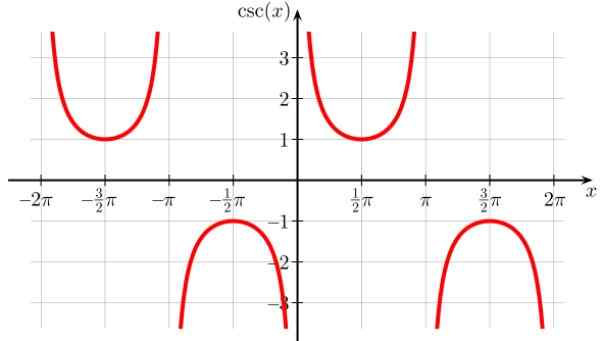Obrázok 8. Funkčný graf f (x) = poškodenie x. Zdroj: Wikimedia Commons. Geek3/cc By-SA (https: // creativeCommons.Org/licencie/By-SA/4.0)

Ublíženie domény x: D = x ∈ R / x ≠ n π; n ∈ Z

Trať na harmóniu: Všetky reais okrem (-1,1)

Cvičenie

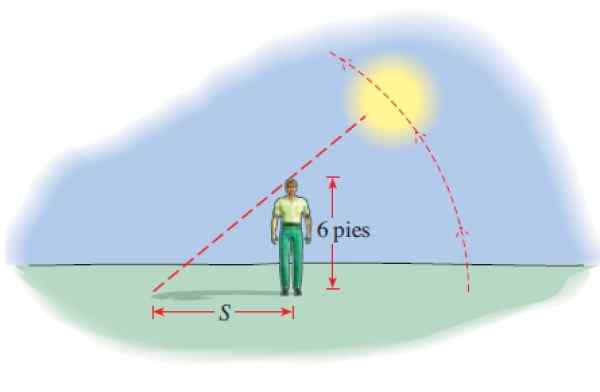
Vysoký muž s výškou 6 -rany vyčnieva tieň, ktorého dĺžka je daná:

S (t) = 6 │cot (π.T/12) │

S S na nohách a t počet hodín po 6:00. Koľko stojí tieň o 8:00, o 12 m, o 14:00 a o 17:45?

Riešenie

Musíme vyhodnotiť funkciu pre každú z daných hodnôt, všimnite si, že absolútna hodnota musí trvať, pretože dĺžka tieňa je pozitívna:

-O 8:00 uplynuli 2 hodiny od 6:00, preto t = 2 a s (t) je:

S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π/6) │pies = 10.39 stôp.

-Keď je to 12 N, T = 6 hodín uplynulo preto:

S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π/2) │pies = 0 stôp. (V tom čase slnko padá zvisle na hlavu osoby).

-O 14:00 strávili t = 8 hodín:

S (8) = 6 │cot (π.8/12) │pies = 6 │cot (2π /3) │pies = 3.46 stôp.

-Keď je 17:45, 11 prešlo 11.75 hodín od 6:00, potom:

S (11.75) = 6 │cot (π x 11.75/12) │pies = 91.54 stôp. V tejto chvíli sa tiene predlžujú dlhšie.

Môže čitateľ vypočítať čas, keď sa tieň osoby rovná jej výške?

Odkazy

1. Carena, m. 2019. Príručka matematiky preduniverzity. Národná univerzita pobrežia.
2. Figuera, J. 1999. Matematika. 1. Diverzifikovaný. Bolivarian Collegiate Editions.
3. Hoffman, J. Výber matematických problémov. Zväzok 4.
4. Jiménez, r. 2008. Algebra. Sála.
5. Zill, D. 1984. Algebra a trigonometria. McGraw Hill.