Matematické funkcie

Matematická funkcia je vzťah medzi dvoma veľkami. Rúno

Čo sú matematické funkcie?

Ten matematické funkcie Sú výrazom v matematickom jazyku vzťahu medzi dvoma premennými a hodnota prvých premenných závisí od druhej. Normálne sú tieto premenné symbolizované písmenami x a y.  Premenná X sa nazýva doména alebo nezávislá premenná; a na y, kodominium alebo závislú premennú.

Pozrime sa na príklad. Máme dve premenné alebo veľkosti: dolár a centy. Vieme, že 100 centov je ekvivalentom dolára. Preto centy (x) sú doména a dolár (y) zodpovedá Codominium. Tento vzťah je možné vyjadriť pomocou nasledujúcej funkcie (F):

F (x) = y / 100

Ak mám vo svojej Piggy Bank 143 centov a chcem vedieť, koľko dolárov som ušetril, uplatňujem iba túto funkciu:

F (x) = 143 /100

Preto mám 1,43 dolárov.

Môžeme tiež vyjadriť inverzný vzťah, to znamená, že dolár zodpovedá 100 centom. V dôsledku toho sa investujú kategórie premenných: dolár (x) sa stáva doménou, zatiaľ čo centy sú kodominium. Týmto spôsobom to vyjadrujeme:

F (x) = x x 100

Ak mám vo svojej Piggy Bank 1,43 dolárov, ale chcem vedieť, koľko centov je toto číslo rovnocenné, stačí uplatniť túto druhú funkciu.

F (x): 1,43 x 100

Výsledok sa vracia k mojim 143 pôvodným centom.

Premenné matematických funkcií

Premenná je jednoducho symbol (x, y, z), ktorý predstavuje rôzne prvky.

V predchádzajúcom príklade premenné X a Y symbolizovali dolár a penny dolára. Ale rovnaké symboly (x a y) sa môžu použiť na reprezentáciu nekonečna prvkov, ako napríklad: vek človeka a jej hmotnosť; Počet letov do určitého cieľa a časové obdobie (týždenne, mesačne, za rok) atď.

Môže vám slúžiť: Syntetické rozdelenie

Premenné možno klasifikovať do mnohých typov, ale najdôležitejšie pre matematické funkcie sú tieto:

• Závislá premenná: tí, ktorých hodnota závisí od hodnoty priradenej k iným premenným v rámci funkcie.
• Nezávislá premenná: Zmeny v tomto type premennej ovplyvňujú hodnoty zvyšku premenných funkcie.
• Kvantitatívna premenná: Je vyjadrená definovanými číselnými množstvami. Môžu to byť celé alebo desatinné čísla.

Charakteristiky matematických funkcií

1- Vzťah medzi premennými je vyjadrený z hľadiska rovnocennosti.

2- pre každú hodnotu premennej x je A a iba ekvivalent premennej a. A naopak: pre určitú hodnotu y existuje A a iba výsledok premennej x.

3- môžu byť graficky reprezentované na karteziánskej rovine, ktorá umožňuje predpovedať správanie jednej z premenných od druhej.

4- Moderná definícia matematickej funkcie je spôsobená nemeckým matematikom Peter Dirichlet (1805-1859), ktorý ju uverejnil v roku 1837.

Typy matematických funkcií

Matematické funkcie možno klasifikovať podľa rôznych kritérií, ako je napríklad vzťah medzi premennými x a y o matematické správanie funkcie.

Medzi hlavné typy patrí:

Algebraické funkcie

Vyznačujú sa vytvorením vzťahu medzi komponentmi, ktoré sú vyjadrené buď monomiálnym alebo polynómom. Tento vzťah sa dá určiť jednoduchými matematickými operáciami, ako je odčítanie, násobenie, delenie, súčet, potenciácia alebo podanie.

Lineárne funkcie

Keď sú zastúpené v karteziánskej rovine, objavujú. Preto ich meno, hoci sú známe aj ako prvé funkcie.

Môže vám slúžiť: spoločný faktor: charakteristiky, príklady, cvičenia

Funkcie na kusy

V tomto type hodnota kodomínium a mení správanie funkcie. Existujú preto dva intervaly s rôznym správaním vo vzťahu k hodnote domény.

Transcendentné funkcie

Sú to veľmi zložité funkcie. Bežné algebraické operácie nestačia (odčítanie, násobenie, delenie, zosilnenie alebo žiarenie) na určenie vzťahu medzi premennými, takže sa musia použiť iné matematické nástroje, ako sú deriváty, integrály alebo logaritms.

Trigonometrické funkcie

Tento typ funkcií ukazuje numerický vzťah, ktorý existuje medzi rôznymi prvkami trojuholníka a inými geometrickými figúrkami, najmä medzi jeho uhlami. Príkladom tohto typu funkcií sú vzorce pre prsník, kosínus, dotyčnicu, secant a harmonte.

Injekčné funkcie

Funkcie tohto typu sú charakterizované osobitosťou vzťahu medzi doménou a kodomínium. Každej z hodnôt z nich zodpovedá iba jedna hodnota domény. Môže sa tiež stať, že hodnota domény nemá v kodomínii žiadnu zodpovedajúcu hodnotu.

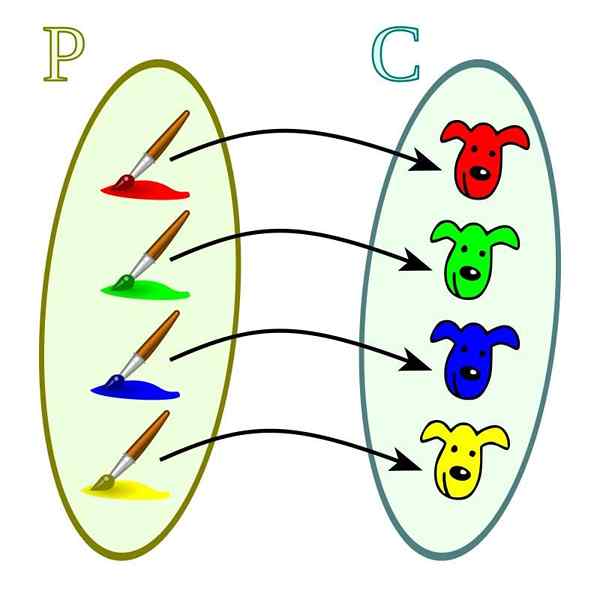Injekčná funkcia. Zdroj: Wikimedia Commons

Injekčné funkcie

V tomto prípade je každá z veľkosti kodomíniu spojená s aspoň jednou z hodnôt domény. Rozlišujú sa od injektívnych funkcií, v ktorých môžu hodnoty kodominium súvisieť s viac ako jednou z hodnoty domény.

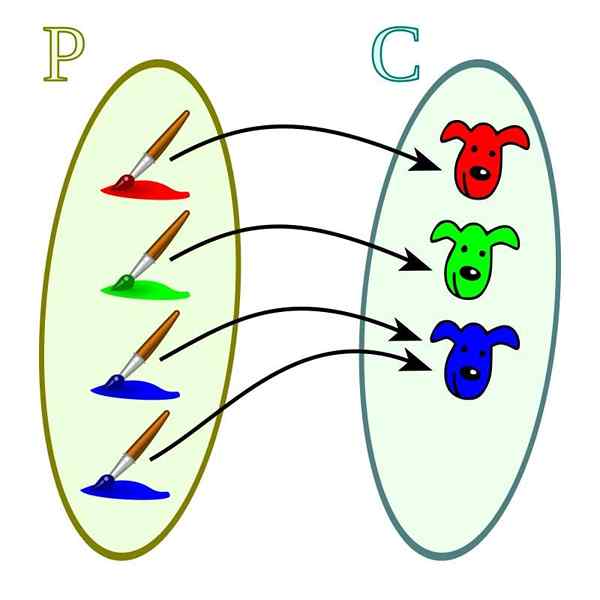Nadmerná funkcia. Zdroj: Wikimedia Commons

Bijektívne funkcie

Tento typ funkcií predstavuje injekčné aj nadmerné vlastnosti.

Čo sú matematické funkcie?

Funkcie sa široko používajú vo všetkých vedách, ktoré majú matematiku ako pomocná veda. Toto je prípad fyziky, inžinierstva, medicíny, financií, štatistík.

Môže vám slúžiť: Distribúcia frekvencie: Ako vytvoriť tabuľku, napríklad cvičenie

V každodennom živote

Môžeme však byť tiež užitoční na riešenie jednoduchších problémov.

Predstavte si, že vám váš starý otec dal 10 mincí, ktoré utratíte za čokoládu. V kiosku ste dali závislú 10 mincí a povedali ste mu, aby vám dal všetky čokolády, ktoré sa dajú kúpiť s týmto množstvom mien. Dali vám 5 čokolády. Aká je cena každého z nich?

Navrhujeme problém: Ak sa 5 čokolády rovná 10 minciam, koľko mincí je rovnocenné s jednou čokoládou?

Naša nezávislá premenná (x) je množstvo čokolády (5), zatiaľ čo závislá premenná (Y) zodpovedá počtu mien, tj 10.

Vyjadrime funkciu nasledovne:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

A už máme odpoveď: každá čokoláda stojí 2 mince.

Odkazy

1. (s/f). Elementárne funkcie. Stránka matematických funkcií. Prevzaté z neúcta.Valfram.com.
2. (s/f). Čo je to funkcia? Prevzaté z Mathsisfun.com.