Funkcie stupňa väčšie ako dva (príklady)

(Polynomial) známky vyššej ako dva má všeobecnú formu:

f (x) = a₀ + do₁x +a₂X² +.. .do_nXⁿ

S n = 3, 4, 5,…, negatívne celé číslo a koeficienty_ani, do₁.._n, ktoré sú zvyčajne skutočné čísla.

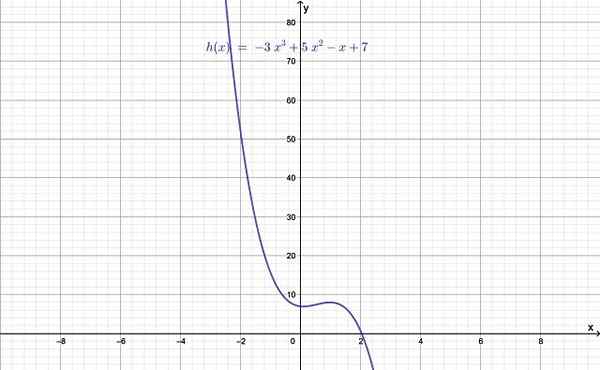postava 1.- Graf funkcie stupňa väčší ako 2. Zdroj: f. Zapata.

Stupeň funkcie je daný hodnotou n, najväčšieho z exponentov a ktorá je zase vyššia ako 2. Keď n = 0 je konštantná funkcia, ak n = 1 je to lineárna funkcia a nakoniec s n = 2 je to kvadratická funkcia.

Príklady funkcií vyšších ako dve, v premennej „x“ sú nasledujúce:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Funkcia f (x) = x³ Je to najjednoduchšie zo všetkých funkcií viac ako dve a jeho stupeň je 3. Stupeň 3 je tiež známy ako kubická funkcia. Pokiaľ ide o svoju časť, G (x) je stupeň 4, pretože je 4 maximálny exponent.

Hodnota N je veľmi dôležitá, pretože určuje všeobecnú formu grafu a tiež maximálne množstvo koreňov alebo priesečníkov, ktoré má funkcia s horizontálnou osou. Funkcia 3 -Grade sa skutočne dotkne horizontálnej osi najviac 3 body, jeden z stupňov 4 to urobí najviac v 4 bodoch atď.

Pokiaľ ide o nezávislý termín, v polynómovej funkcii akéhokoľvek stupňa označuje priesečník funkcie s vertikálnou osou.

Charakteristiky polynómových funkcií viac ako dve

Oblasť

Doménou funkcie je sada hodnôt, ktoré umožňujú výpočet hodnôt y = f (x). Pre polynómové funkcie je táto sada nastavená na skutočné čísla N alebo súbor komplexných čísel, ak je to potrebné na rozšírenie domény.

Môže vám slúžiť: trigonometrické limity: Ako ich vyriešiť, vyriešené cvičenia

Znamená, že vzhľadom na polynomickú funkciu f (x) = a₀ + do₁x +a₂X² +.. .do_nXⁿ, Vždy môžete nahradiť akékoľvek skutočné číslo, vykonávať uvedené operácie a získať v dôsledku hodnoty skutočného y = f (x) real.

Rozsah

Je to sada tvorená všetkými hodnotami získanými f (x), to znamená, že obrázky, ktoré má každá hodnota x prostredníctvom funkcie f (x). Pre polynómové funkcie väčšie ako 2 je táto sada reálnych čísel.

Korene funkcie

Sú hodnoty x, pre ktoré sa splní, že f (x) = 0. Ako je uvedené vyššie, stupeň funkcie označuje maximálny počet koreňov, ktoré môže mať, hoci nie všetky sú nevyhnutne skutočné.

Ak sú koeficienty funkcie reálne čísla, skutočné korene zodpovedajú priesečníkom funkcie s osou x.

Príklad 1

Racionálne korene funkcie f (x) = 2x³ - 9x² + 7x + 6 nájdete prostredníctvom nasledujúcej vety:

Ak je koreň f (x) = a₀ + do₁x +a₂X² +.. .do_nXⁿ Je to forma B/C, takže možné hodnoty B sú faktory a_ani a možné hodnoty C sú faktory a_n.

Pre funkciu príkladu sú už zjednodušené kombinácie: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Teraz je každý testovaný napríklad prostredníctvom postupu syntetického delenia. Ak je zvyšok divízie 0, preukázaná hodnota je koreňom:

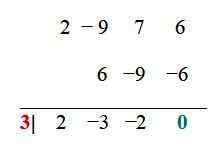
Hodnota x₁ = 3 je koreň alebo nula funkcie, preto (x - 3) je bežným faktorom f (x), a to je možné písať ako:

Môže vám slúžiť: Unitárny kruh: trigonometrické funkcie a aplikácie

f (x) = (x - 3) ∙ (2x² −3x −2)

Zostávajúce dva korene sú hodnoty, ktoré spĺňajú 2x rovnicu² −3x −2 = 0. Túto rovnicu je možné vyriešiť prostredníctvom všeobecného vzorca, vedeckej kalkulačky alebo opakovania predchádzajúceho procesu Tanteo.

Tieto korene sú x₂ = 2 a x₃ = - ½ a teraz F (x) možno písať ako produkt troch faktorov:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Križovatky f (x) s osou x sú body: P₁ (3,0), p₂(2.0) a P₃(−½, 0). Graf funkcie, získaný s geogebra, ukazuje jeho križovatky s osou X:

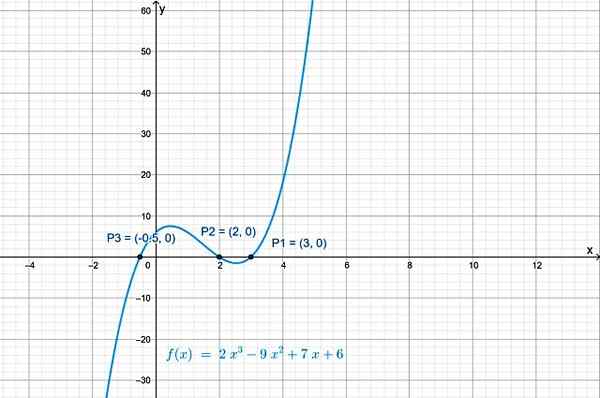Obrázok 2.- Polynomická funkcia stupňa 3 má tri križovatky s horizontálnou osou. Zdroj: f. Zapata.

Križovatka s vertikálnou osou

Ak chcete nájsť priesečník funkcie s vertikálnou osou, musíte nájsť f (0), čo je jednoducho₀.

Príklad 2

Nájdite križovatku f (x) = 2x³ - 9x² + 7x + 6 s vertikálnou osou je veľmi jednoduchý, keď sa získa x = 0 v f (x), získa sa:

f (x) = 6

A bod priesečníka funkcie s vertikálnou osou je p₄(0,6).

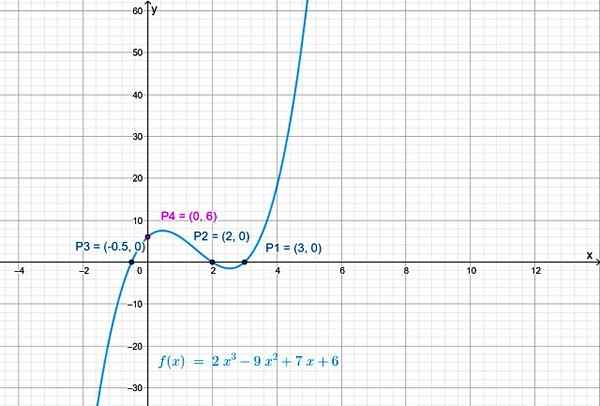Obrázok 3. Priesečník krivky s vertikálnou osou vytvára x = 0 v f (x). Zdroj: f. Zapata.

Kontinuita

Polynomické funkcie všeobecne a najmä funkcie vyšších ako 2 sú kontinuálne funkcie v celej svojej doméne, to znamená, že nemajú žiadne skoky, kroky, diery alebo hodnoty, pre ktoré nie sú definované. Nemajú ani asymptoty, ktoré sú vertikálne, vodorovné alebo šikmé priamo, ku ktorému sa funkcia blíži bez toho, aby ich prekročila.

Tieto vlastnosti jemnosti a kontinuity sú ocenené v grafoch uvedených vyššie.

Graf funkcií vyšších ako 2

Grafy funkcií vyšších ako 2 sú nepretržité a mäkké a ich tvar závisí od stupňa polynómu.

Môže vám slúžiť: Permutácie bez opakovania: vzorce, demonštrácia, cvičenia, príklady

Napríklad tie, ktoré sú v stupni 3, má negatívny znak v termíne s najvyšším stupňom).

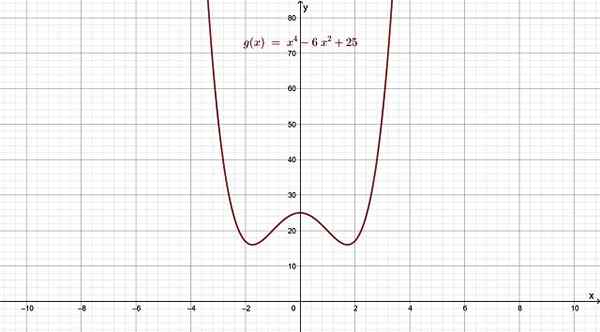Obrázok 4. Polyinomická funkcia stupňa 4, ktorej graf pripomína písmeno w. Zdroj: f. Zapata.

Pre hodnoty x ďaleko od x = 0, vľavo aj vpravo, sa funkcia správa, ako by to robil termín najväčšieho stupňa, pretože to prevláda pred ostatnými, keď X sa stane veľmi veľký alebo veľmi malý.

Na obrázku, ktorý sleduje funkciu f (x) = 2x, sa porovnáva³ - 9x² + 7x + 6 s funkciou r (x) = x³ A oceňuje sa, že tvar oboch kriviek je podobný hodnotám x, ktoré sú ďaleko od x = 0.

Pre veľké hodnoty X funkcia rýchlo rastie tým, že má tendenciu na +∞, zatiaľ čo pre záporné hodnoty X funkcia rýchlo klesá a má tendenciu −∞.

Obrázok 5.- Všetky funkcie stupňa n sa správajú podobne, keď sa pohybujú od x = 0, vľavo aj vpravo. Zdroj: f. Zapata.

Porovnanie kriviek momentového momentu (obrázok 4) s nepárnym stupňom (obrázok 2), pokiaľ koeficient, ktorý sprevádza termín s najvyšším stupňom, má rovnaké znamenie, zistilo sa, že krivky nepárneho stupňa začínajú „y“ negatívne a rast, zatiaľ čo v cieľovom stupni začínajú „y“ pozitívne a znižujú sa.

Odkazy

1. Barnett, r. 2000. Predbežné precudzenie: Funkcie a grafika. 4. Vydanie. McGraw Hill.
2. Kalkulácia.Dc. Polynomické funkcie. Obnovené z: výpočtu.Dc.
3. Larson, R. 2012. Predbežné vyfarbenie. 8. Vydanie. Učenie sa.
4. Stewart, J. 2007. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
5. Rozmanitosť. Grafické polynomické funkcie. Zdroj: WarsityTorm.com.