Vlastnosti exponenciálnej funkcie, príklady, cvičenia

Ten exponenciálna funkcia Je to matematická funkcia veľkej dôležitosti pre mnohé aplikácie, ktoré má. Je to definované takto:

f (x) = b^X, S b> 0 a b ≠ 1

Kde B je skutočná konštanta vždy pozitívna a odlišná od 1, ktorá je známa ako základňa. Všimnite si, že skutočná premenná X sa nachádza v exponent, Týmto spôsobom je F (x) vždy skutočným číslom.

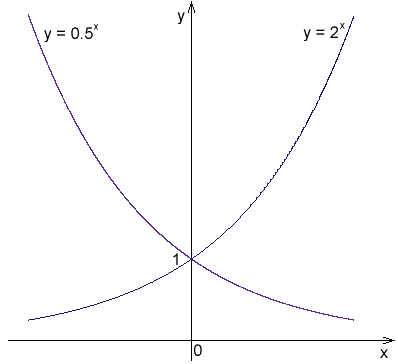postava 1. Exponenciálne funkcie so základňami 2 a 1/2

Príklady exponenciálnych funkcií sú nasledujúce:

-f (x) = 2^X

-g (x) = 5 šce^-3x

-H (x) = 4 šcela (10^2x)

Sú to funkcie, ktoré rastú - alebo znižujú, podľa znaku exponentu - veľmi rýchlo, takže sa hovorí o „exponenciálnom raste“, keď sa určitá veľkosť zvýši veľmi rýchlo. Preto sú vhodné na modelovanie rastu živých bytostí, ako sú baktérie.

Ďalšou veľmi zaujímavou aplikáciou je použitie zloženého záujmu. Čím viac peňazí máte na účte, tým viac záujmov a môžu vypočítať každý určitý časový interval, tak malý, ako chcete.

S pomocou logaritmickej funkcie, ktorá je inverznou funkciou exponenciálneho, môže byť známa po tom, ako dlho sa určitý kapitál zvyšuje na určitú hodnotu.

[TOC]

Vlastnosti exponenciálnej funkcie

Obrázok 2. Príklady exponenciálnych funkcií. Zdroj: f. Zapata.

Nasledujú všeobecné vlastnosti akejkoľvek exponenciálnej funkcie:

-Graf akejkoľvek exponenciálnej funkcie vždy pretína vertikálnu os v bode (0,1), ako je vidieť na obrázku 2. Je to preto, že b⁰ = 1 pre akúkoľvek hodnotu B.

-Exponenciálna funkcia sa nepretína na osi x, v skutočnosti je táto os horizontálnou asymptotom pre funkciu.

-Pretože B¹ = b, bod (1, b) vždy patrí do funkčnej grafiky.

Môže vám to slúžiť: hepagonálny hranol

-Doménou exponenciálnej funkcie je sada reálnych čísel a f (x) = b^X Je nepretržitý vo celej svojej doméne.

-Rozsah exponenciálnej funkcie je všetky reálne čísla väčšie ako 0, čo sa tiež zaznamenávajú s grafikou.

-Exponenciálna funkcia je jeden po druhom, to znamená, že každá hodnota x patriacou k doméne funkcie má jedinečný obraz v množine príchodu.

-Inverzia exponenciálu je logaritmická funkcia.

Konkrétne vlastnosti exponenciálnej funkcie

Ako sme už povedali, exponenciálna funkcia sa môže zvyšovať alebo klesať.

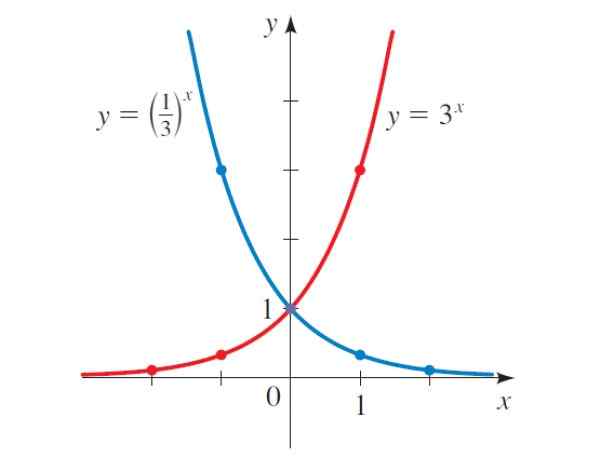
Ak je graf na obrázku 2 starostlivo preštudovaný, poznamenáva, že ak b> 1, funkcia rastie, napríklad y = 3^X, Ale v prípade y = (1/3)^X, s B < 1, la función decrece.

Máme dva typy exponenciálnych funkcií s týmito konkrétnymi vlastnosťami:

Pre b> 1

-Funkcia vždy rastie.

-Keď sa zvýši hodnota B, funkcia rastie rýchlejšie, napríklad y = 10^X rastie rýchlejšie ako y = 2^X.

-Ak je premenná vyššia ako 0, funkcia získa hodnoty väčšie ako 1, to znamená:

Pre x> 0: y> 1

-A ak x<0, entonces f(x) < 1.

Za b < 1

-Funkcia vždy klesá.

-Znížením hodnoty B sa funkcia stále rýchlejšie znižuje. Napríklad y = (1/5)^X klesá rýchlejšie ako y = (1/3)^X.

-Pre hodnoty x nižšie ako 0, funkcia má hodnoty väčšie ako 1, to znamená:

Pre x 1

-Nakoniec, keď x> 0, potom a < 1.

Príklady exponenciálnych funkcií

Exponenciálna funkcia je veľmi užitočná pre modelovanie javov vo vede a hospodárstve, ako uvidíme nižšie:

Prírodná exponenciálna funkcia

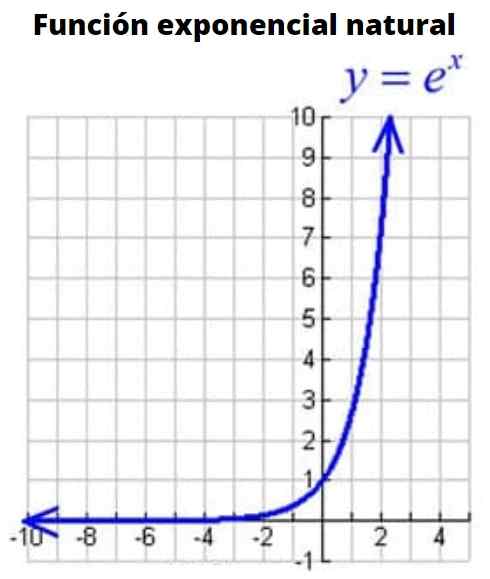Obrázok 3: Graf prírodnej exponenciálnej funkcie

Je to funkcia, ktorej základňa je číslo E alebo Eulera, iracionálne číslo, ktorého hodnota je:

Môže vám slúžiť: doplnkové uhly: čo sú, výpočet, príklady, cvičenia

E = 2.718181828…

Táto základňa, aj keď to nie je okrúhle číslo, funguje veľmi dobre pre množstvo aplikácií. Preto sa považuje za najdôležitejší základ zo všetkých exponenciálnych funkcií. Prírodná exponenciálna funkcia je vyjadrená matematickým spôsobom ako:

f (x) = e^X

Exponenciálna funkcia sa často objavuje v pravdepodobnosti a štatistike, pretože rôzne distribúcie pravdepodobnosti, ako je normálne rozdelenie, Poisson a ďalšie, sa dajú vyjadriť prostredníctvom exponenciálnych funkcií.

Nepretržitý úrok

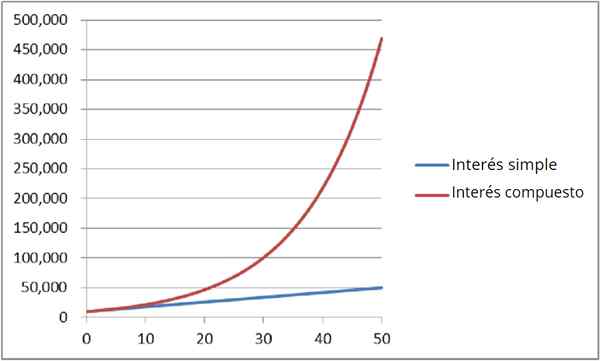Obrázok 4: Porovnanie jednoduchého a zloženého záujmu

Volá sa to tiež Nepretržitá kapitalizácia. Poznať množstvo peňazí Do Máš po tón Roky, používa sa exponenciálny výraz:

A (t) = p ⋅ e^Rt

Kde P je suma pôvodne uložených peňazí, R je úroková sadzba ročne a nakoniec tón je počet rokov.

Rast baktérií

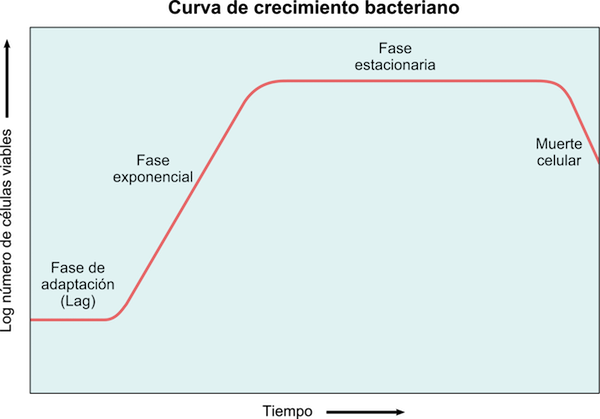Obrázok 5: Bakteriálna krivka rastu, kde sa pozoruje latencia, exponenciálne, stacionárne a smrteľné fázy

Baktérie rastú exponenciálne, takže rast možno modelovať pomocou:

N (t) = n_ani ⋅ E ^Kt

Kde n (t) je existujúca populácia po čase t (takmer vždy v hodinách), n_ani Je to počiatočná populácia a K je konštanta, ktorá závisí od bakteriálneho typu a podmienok, za ktorých sú k dispozícii živiny.

Rádioaktívny rozklad

Niektoré jadrá v prírode sú nestabilné, takže sa odmietajú transformovať na stabilnejšie, proces, ktorý môže byť veľmi stručný alebo trvá tisíce rokov, v závislosti od izotopu. Počas rádioaktívneho rozkladu sa emitujú a niekedy aj fotóny.

Niektoré rádioaktívne izotopy majú lekárske aplikácie, napríklad rádioaktívny jód I-131, ktoré lekári používajú pri diagnostike a liečbe určitých podmienok štítnej žľazy.

Rádioaktívny rozklad je modelovaný exponenciálnou funkciou.

Môže vám slúžiť: Koľko desatín je v jednotke?

Vyriešené cvičenia

Rovnice, v ktorých sa neznámy javí ako exponent, sa nazývajú exponenciálne rovnice. Na vyčistenie hodnoty neznáma sa používajú rôzne algebraické manipulácie a použitie funkcie logaritmu, čo je opačná funkcia exponenciálneho.

Pozrime sa na niektoré vyriešené cvičenia, ktoré ilustrujú bod.

- Cvičenie 1

Vyriešte nasledujúce exponenciálne rovnice:

do 5^X = 625

b) 5^X = 2^X-1

Roztok

Číslo 625 je násobok 5, v skutočnosti, keď ho rozkladáme, zistíme, že:

625 = 5⁴

Preto môžeme napísať:

5^X = 5⁴

Pretože základne sa rovnajú ľavej aj pravej, môžeme zladiť exponenty a získať:

x = 4

Riešenie B

Pre toto cvičenie sa nemôžeme uchýliť k predtým použitej technike, pretože základy nie sú rovnaké. Týmto spôsobom však môžeme aplikovať logaritmus na oboch stranách rovnosti:

5^X = 2^X-1

Protokol (5^X) = log (2^X-1)

Teraz sa uplatňuje nasledujúca vlastnosť logaritmov:

Protokol mⁿ = n⋅log m

A zostáva:

x⋅log 5 = (x-1) ⋅log 2

x⋅ (log 5 - log 2) = -log 2

x = - log 2 ÷ (log 5 - log 2)

- Cvičenie 2

Uveďte, akú funkciu každý z grafov uvedených nižšie zodpovedá:

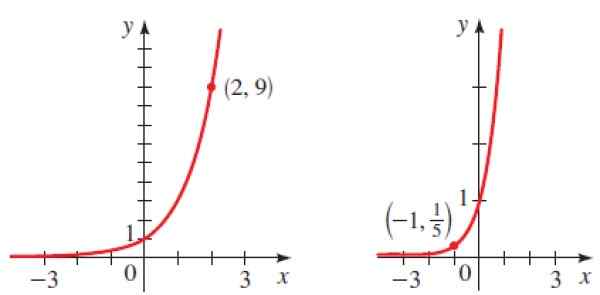Obrázok 6. Grafika parast Exponenciálne funkcie rozlíšeného cvičenia 2. Zdroj: Stewart. J. Predbežné vyfarbenie.

Roztok

Keďže ide o rastúci graf, B je väčší ako 1 a vieme, že bod (2.9) patrí do grafu:

y = b^X → 9 = B²

Vieme, že 3² = 9, preto b = 3 a funkcia je y = 3^X

Riešenie B

Opäť nahradíme daný bod (-1, 1/5) na y = b^X získať:

1/5 = B^-1 = 1/b

Potom b = 5 a vyhľadávanou funkciou je:

y = 5^X

Odkazy

1. Figuera, J. 2000. Matematika 1. Diverzifikovaný. Edície Co-Bo.
2. Gid Hoffmann, J. Výber matematických problémov pre 4. Rok. Edimatizovať. Sphinx.
3. Jiménez, r. 2008. Algebra. Sála.
4. Larson, R. 2010. Výpočet premennej. 9NA. Vydanie. McGraw Hill.
5. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.