Klesajúca funkcia Ako ju identifikovať, príklady, cvičenia

A klesajúca funkcia f je ten, ktorého hodnota klesá so zvyšovaním hodnoty x. Znamená, že v danom intervale, berúc do úvahy dve hodnoty x₁ a x₂ tak, že x₁ < x₂, potom f (x₁)> f (x₂).

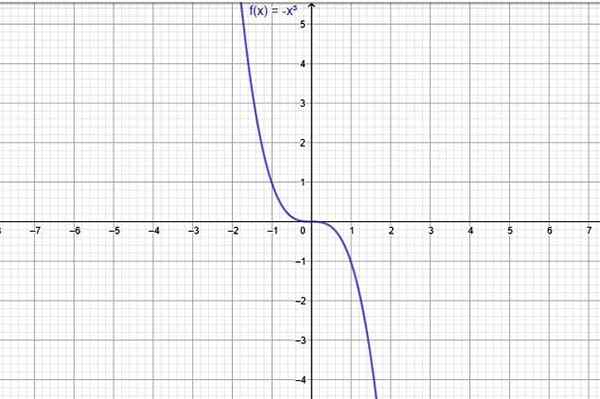
Príkladom funkcie, ktorá sa vždy znižuje, je f (x) = -x³, ktorého graf ukazuje na nasledujúcom obrázku:

postava 1. Funkcia, ktorá vždy klesá v celej jeho doméne, je f (x) = -x^3. Zdroj: f. Zapata cez geogebra.

Aj keď niektoré funkcie, ako je táto, sa vyznačujú znížením celej svojej domény, nie všetky sa správajú takto, zvyšujú sa a tiež tie, ktoré rastú a znižujú určité intervaly domény. Štúdium intervalov rastu a zníženia sa nazýva monotónnosť funkcia.

Podobne sa rast alebo zníženie funkcie môže zvážiť v určitom doméne. Ale akákoľvek funkcia, ktorá v danom intervale klesá, je tiež v každom bode, ktorý k nej patrí.

[TOC]

Ako identifikovať klesajúcu funkciu?

Funkčný graf označuje vizuálne, či klesá alebo nie. Ak sa pri pohybe v rastúcom zmysle X „zostupuje“, znamená to, že klesá.

A ak máte intervaly, v ktorých klesá a rastie striedavo, čo je najbežnejšie, pretože sú jasne odhalené pozorovaním správania funkcie v jej doméne, pretože budú intervaly, v ktorých funkcia „vystúpi“ a ďalšie v ktoré „zostup“.

Alternatívne, ak funkčný graf nie je k dispozícii, analyticky je možné určiť, či klesá v jednom bode alebo v intervale, prostredníctvom prvého derivátu.

Kritérium prvého derivátu

Všimnite si správanie klesajúcej funkcie znázornenej na obrázku 2. Segmenty ružovej čiary sú dotýkajúce sa bodov, ktorých súradnice sú [a, f (a)] a [A+h, f (a+h)] a mať negatívny svah.

Môže vám slúžiť: Ako sa informácie získajú v prieskume?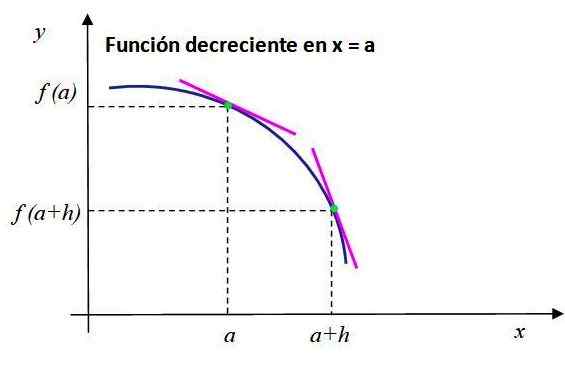Obrázok 2. Sklon tangentovej čiary k grafu f (x) je záporný pri x = a, potom funkcia v tomto bode klesá. Zdroj: f. Zapata.

Pre túto funkciu je splnené nasledujúce:

F (a+h) - f (a) < 0 ⇒  F (a+h) < f (a)

Preto sa dá predpokladať, že funkcia klesá x = a.

Prvý odvodený z funkcie F (x), vyhodnotený pri x = a, čo je podľa definície sklonom dotyčnice k krivke pri x = a, je daný:

Limit naznačuje, že hodnota H sa môže vykonať tak malá, ako chcete, a naznačuje, že znamenie fa), Môže sa použiť na to, aby vedel, či funkcia klesá v konkrétnom bode, pokiaľ derivát v tomto bode existuje.

Potom áno fa) < 0, Je možné potvrdiť, že funkcia klesá a naopak, ak f '(a)> 0, Potom funkcia v tomto bode rastie.

Veta na zníženie a rastúce funkcie

Predtým sa odkazoval na správanie funkcie v bode. Teraz nasledujúca veta umožňuje poznať intervaly, v ktorých funkcia klesá, rastie alebo konštanta:

Nech f je diferencovateľná funkcia v intervale (a, b). Je pravda, že:

-Áno f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Ak je naopak f '(x)> 0 pre všetky x patriace (a, b), hovorí sa, že funkcia f (x) rastie v (a, b).

-Nakoniec, ak f '(x) = 0 pre všetky x, ktoré patrí do intervalu (a, b), f (x) je v uvedenom intervale konštantný.

Demonštrácia

Predpokladajme, že f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ a x₂ patriaci k uvedenému intervalu a podmienky, že x₁< x₂.

Priemerná veta hodnoty uvádza, že medzi x existuje skutočné číslo C₁ a x₂, také:

Môže vám slúžiť: spoločný faktor pre zoskupovanie podmienok: príklady, cvičenia

Ako je stanovené od x₁< x₂,  Δx je pozitívny. Takže, keď je f '(c) negatívny, takže Δy je tiež. Preto f (x₁) je väčší ako f (x₂) A funkcia účinne klesá vo všetkých bodoch intervalu (a, b).

Kroky na zistenie, či funkcia klesá

Ak chcete nájsť intervaly poklesu a rastu funkcie použitím predchádzajúcej vety, nasledujú tieto kroky:

-Nájdite prvý odvodený z funkcie a priraďte ju na nulu, pričom vyriešite výslednú rovnicu. Určte tiež body, v ktorých derivát neexistuje.

Všetky tieto body sa volajú kritické body A je potrebné ich nájsť, pretože v nich má derivát príležitosť zmeniť svoje znamenie, čo naznačuje, že funkcia prechádza z rastúceho k zníženiu alebo naopak.

-Doména funkcie je rozdelená do intervalov určených bodmi, v ktorých je prvý derivát zrušený alebo neexistuje.

-Nakoniec sa znak derivátu študuje v ľubovoľnom bode, ktorý patrí do každého z intervalov získaných v predchádzajúcom kroku.

Príklady klesajúcich funkcií

Funkcie sa všetky neznižujú rovnakým tempom, niektoré to robia rýchlejšie ako iné. Nasledujúce funkcie, ktoré sa v praxi často objavujú, sa znižujú:

Exponenciálna funkcia

Funkcia formy f (x) = a^X, S A medzi 0 a 1, bez týchto, rýchlo sa znižuje v ich doméne.

Funkcia 1/x

Prostredníctvom online grafického programu ako geogebra je zostavený graf funkcie F (x) = 1/x, čo potvrdzuje, že klesá v celej jeho doméne.

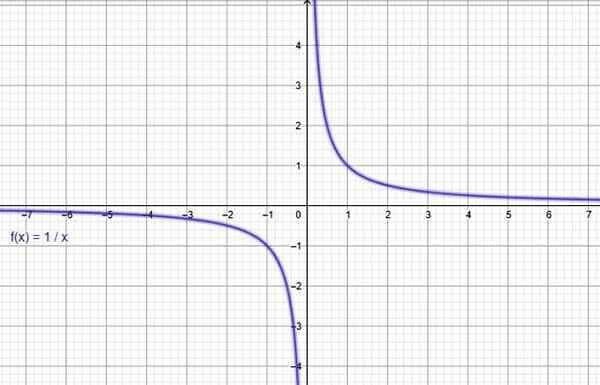Obrázok 3. Funkcia f (x) = 1/x klesá. Zdroj: f. Zapata cez geogebra.

Súvisiaca funkcia

Funkcie formy y = mx + b s m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Môže vám slúžiť: matematická rovnosť

Cvičenie

Nájdite, ak existujú, intervaly zníženia funkcie:

f (x) = x⁴ - 6x² - 4

Riešenie

Prvým krokom je nájsť f '(x):

f '(x) = 4x³ - 12x

Prvý derivát F (x) je kontinuálna funkcia, to znamená, že nemá žiadne body diskontinuity, ale je zrušený v:

4x³ - 12x = 0 = 4x (x²-3) = 0

Riešenia tejto rovnice sú: x₁ = 0, x₂ = - √3 a x₃ = √3. Toto sú kritické body, ktoré v intervaloch rozdeľujú doménu F (x): (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Potom sa vyhodnotí prvý odvodený v ľubovoľnej hodnote x, ktorá patrí do každého intervalu. Tieto hodnoty boli vybrané:

Pre (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

Pre (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

Pre (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Pre (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Rovnako ako niekoľko intervalov, je dobré vytvoriť tabuľku na usporiadanie výsledkov. Šípka nahor naznačuje, že funkcia rastie a klesá, čo klesá:

Dospelo sa k záveru, že funkcia klesá v intervaloch (-∞,- 3) a (0, √3) a rastie v zostávajúcich intervaloch. Pôvodná funkcia v geogebre sa ľahko skontroluje grafom.

Odkazy

1. Ayres, f. 2000. Kalkulácia. 5ed. MC Graw Hill.
2. Leithold, L. 1992. Výpočet analytickou geometriou. Harla, s.Do.
3. Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia. Mexiko: Pearson Education.
4. Matemobile. Funkcie, rastúce, klesajúce a konštantné. Získané z: Matemovil.com
5. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.