Rastúca funkcia Ako ju identifikovať, príklady, cvičenia

Máte jedného rastúca funkcia Keď sa hodnota y zvýši, ak sa X tiež zvyšuje, na rozdiel od klesajúcich funkcií, v ktorých hodnota a klesá, keď sa X zvyšuje.

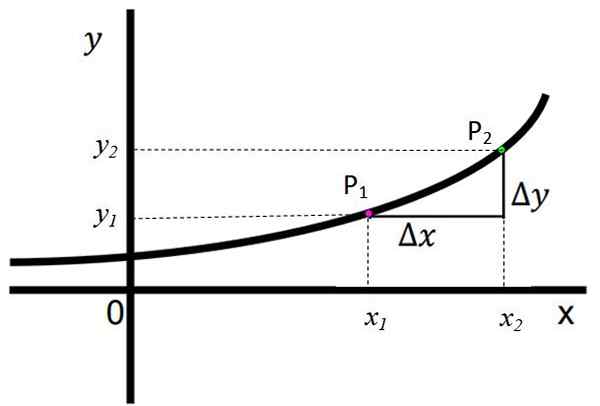
Nasledujúci obrázok ukazuje rastúcu funkciu a je jasne pozorované, že keď sa pohybuje zľava doprava na osi X, hodnota príslušného súradnice a ekvivalent k F (x) sa postupne zvyšuje. Hovorí sa, že ak pre všetko x₂ > x₁, Potom existuje a₂ > a₁.

postava 1. Rastúca funkcia. Zdroj: f. Zapata.

Body P₁ A p₂ Sú zobrazené, majú súradnice (x₁, a₁) a (x₂,a₂). Sú definované:

Δy = y₂ -a₁

Δx = x₂ -X₁

V tejto funkcii majú Δy aj δx pozitívne znamenie, čo znamená a to a₂ > a₁ a x₂ > x₁, respektíve. To je jasný znak toho, že funkcia efektívne rastie.

Dobrým príkladom vždy rastúcej funkcie (zvyšujúce sa monotónne) je Neperian Logaritmus skutočného čísla. Čím vyššie je číslo, tým väčší je jeho logaritmus.

[TOC]

Ako identifikovať rastúcu funkciu?

V jednoduchej a kontinuálnej funkcii, ako je znázornené na obrázku 1, je ľahké určiť, či sa funkcia zvyšuje alebo klesá za predpokladu, že graf je k dispozícii.

V niektorých intervaloch však môžu rásť zložitejšie funkcie. Preto hovoríme o tom Intervaly rastu a znížiť funkcia.

V sieti je bezplatná online grafika, napríklad Geogebra, ktorá umožňuje grafy všetkých druhov funkcií. Ak má graf, je ľahké určiť, či sa funkcia neustále zvyšuje, napríklad F (x) = log x alebo či má intervaly, v ktorých rastie, a iné, v ktorých klesá a čo je.

Kritérium prvého derivátu

Ak vezmeme do úvahy určitý numerický interval i, ak je kvocient medzi množstvami δy a Δx pozitívny, funkcia sa zvyšuje. A naopak, ak je negatívna, funkcia klesá.

Môže vám slúžiť: Pravdepodobnosť frekvencie: koncept, ako sa vypočíta a príklady

Musíš:

Δy / δx> 0 → Rastúca funkcia

Skutočnosť, že Δy / δx> 0 a funkcia sa zvyšuje v určitom intervale, naznačuje, že prvý odvodený z funkcie alebo skôr jej znamenie sa môže použiť ako kritérium na určenie, či je v skutočnosti v skutočnosti, funkcia rastie v konkrétnom interval alebo dokonca v určitom bode vašej domény.

Prvý derivát je skutočne definovaný ako sklon krivky v každom bode:

Čo znamená, že δx sa dá urobiť tak malá, ako chcete. Ak f '(x)> 0 pre určitú hodnotu x, napríklad x = a, sklon krivky v tomto bode f' (a) je pozitívny a funkcia sa tam zvýši.

Nasledujúca veta ponúka kritérium, aby ste vedeli, kedy funkcia v intervale rastie (a, b):

Veta

Nech f (x) je odvoditeľnou funkciou v (a, b). Ak f '(x)> 0, pre akúkoľvek hodnotu x patriacej do uvedeného intervalu sa hovorí, že F (x) rastie v (a, b).

Veta sa používa na zistenie, v ktorých intervaloch rastie funkcia, podľa týchto krokov:

Krok 1

Nájdite body, v ktorých f '(x) = 0, ako aj tie, v ktorých neexistuje f' (x). Títo, nazývaní kritické body, Toto sú body, keď F '(x) môže zmeniť znamenie, a preto má F (x) príležitosť presunúť sa z rastúceho k klesajúcemu alebo naopak.

Krok 2

Nájdite znak f '(x) pre ľubovoľnú hodnotu v každom z intervalov určených bodmi zistenými v kroku 1.

Krok 3

Použite vetu, aby ste vedeli, či funkcia rastie alebo nie v každom intervale.

Príklady rastúcich funkcií

Existujú funkcie, ktoré majú určité intervaly rastu a iné poklesy, ale tie, ktoré sú uvedené nižšie, vždy rastú.

Váha založená na veku

Hmotnosť osoby od jej narodenia, až do približne ukončenia dospievania, je takmer vždy rastúcou funkciou veku. Dojčatá a deti rastú a vyvíjajú sa v priebehu rokov a potom, keď sa dostanú do dospelosti, očakáva sa, že zvyšok ich života si zachová stabilnú váhu, hoci vzostupy a pády sú veľmi časté.

Môže vám slúžiť: vertikálna čiara

Funkcia logaritmu

Funkcie skutočného variabilného logaritmu Neperian F (x) = ln x a desatinný logaritmus f (x) = log x vždy rastú.

Funkcia druhej koreňovej funkcie skutočného čísla

Ďalšou funkciou, ktorá vždy rastie, je funkcia druhej druhej koreňa kladného čísla:

y = √x

Súvisiaca funkcia a lineárna funkcia

Súvisiaca funkcia:

f (x) = mx + b

Rastie vždy, keď je čiara pozitívny svah. Podobne identita a lineárne funkcie:

f (x) = x a f (x) = ax, s> 0

Rastú v celej svojej doméne.

Exponenciálna funkcia

Exponenciálna funkcia ako F (x) = e^X  A vo všeobecnosti funkcia formulára:

f (x) = a^X, S> 1

Rastú v celej svojej doméne.

Funkcia indexu potenciálneho imparu

Potenciálne funkcie nepárneho exponentu, ako sú tieto:

• f (x) = x³
• g (x) = x⁵

Vždy rastú.

Cvičenia

Cvičenie 1

Určite, v ktorých intervaloch funkcia znázornená v nasledujúcom grafe sa zvyšuje:

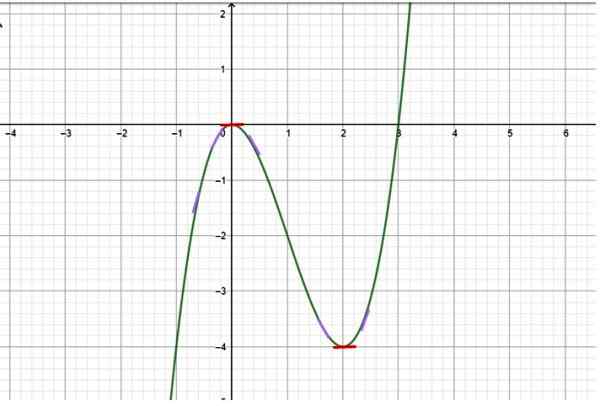Obrázok 2. Funkcia s rastovým a znížením intervalov. Zdroj: f. Zapata.

Riešenie

Keď je graf k dispozícii, z jeho starostlivého pozorovania sa zistí, že funkcia má nasledujúce správanie:

-Z x → -∞ do x = 0 funkcia sa zvyšuje, pretože hodnoty y sa stávajú čoraz menej negatívnymi. Segmenty malých svahov boli nakreslené vo fialovej farbe, aby sa označili sklon dotykovej čiary k krivke v rôznych bodoch (sklon dotyčnice k krivke je presne jeho prvý derivát).

Tieto segmenty majú pozitívny sklon, takže veta zaisťuje, že funkcia v tomto intervale rastie.

-Ale pri x = 0 je sklon krivky zrušený, ktorý je označený malým horizontálnym červeným segmentom. Toto je kritický bod funkcia.

Môže vám slúžiť: Čo sú matematika a na čo sú pre to? 7 Dôležité aplikácie

Odtiaľ sa funkcia začína znižovať a stáva sa negatívnejšími hodnotami a. Táto situácia pokračuje až do X = 2, čo je ďalší kritický bod.

Potom v intervale z x = 0 do x = 2 funkcia klesá.

-Z x = 2 sa funkcia stáva čoraz menej negatívnou, až kým x = 3 neprekročí os x a zakaždým sa stáva pozitívnejšou. Preto je to interval rastu.

Záver: Intervaly rastu sú (-∞, 0) a (2, ∞+), zatiaľ čo interval zníženia je (0,2).

Cvičenie 2

Stanovte intervaly rastu nasledujúcej funkcie prostredníctvom kritérií prvého derivátu:

f (x) = x² - 2x

Riešenie

Podľa vyššie uvedených krokov sa vypočíta prvý derivát a rovná sa 0, aby sa našli kritické body:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Táto hodnota určuje existenciu intervalov (-∞, 1) a (1, ∞+). Zvolené sú dve ľubovoľné hodnoty, ktoré patria ku každému z nich:

-Pre x = 0, ktoré patrí do (-∞, 1), musíte f '(0) = 2.0 - 2 = -2. V dôsledku výsledku je negatívny, funkcia v tomto intervale klesá.

-Pre x = 3, ktoré patrí do (1, ∞+), je prvý derivát hodnotený f '(3) = 2.3 - 2 = 4. Pretože výsledok je pozitívny, dospelo sa k záveru, že funkcia rastie v tomto intervale.

Čítačka môže grafovať pôvodnú funkciu f (x) = x² - 2x na online grafiku na potvrdenie tohto výsledku.

Odkazy

1. Ayres, f. 2000. Kalkulácia. 5ed. MC Graw Hill.
2. Leithold, L. 1992. Výpočet analytickou geometriou. Harla, s.Do.
3. Purcell, e. J., Varberg, D., & Rigdon, s. A. (2007). Kalkulácia. Mexiko: Pearson Education.
4. Matemobile. Funkcie, rastúce, klesajúce a konštantné. Získané z: Matemovil.com
5. Requena, b. Rastúce funkcie. Získané z: Universoformulas.com.
6. Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.