Funkcia konštantných charakteristík, príklady, cvičenia

Ten konštantná funkcia Je to ten, v ktorom hodnota a. Inými slovami: Konštantná funkcia má vždy formu  f (x) = k, kde klimatizovať Je to skutočné číslo.

Grafovaním konštantnej funkcie v súradnicovom systéme Xy, Je to vždy priamka rovnobežná s vodorovnou osou alebo osou X.

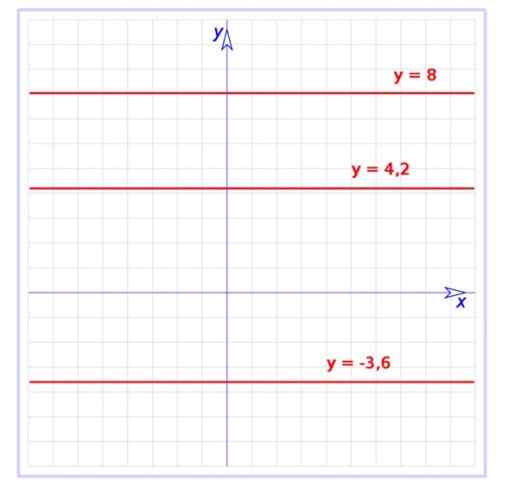
postava 1. Graf niekoľkých konštantných funkcií na karteziánskej rovine. Zdroj: Wikimedia Commons. Používateľ: hite [verejná doména]

Táto funkcia je konkrétny prípad príbuzná funkcia, ktorého graf je tiež priamka, ale so svahom. Konštantná funkcia má nulovú čakajúcu, to znamená, že je to vodorovná čiara, ako je vidieť na obrázku 1.

Existuje graf troch konštantných funkcií:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Všetky sú rovné rovnobežne s vodorovnou osou, prvá je pod touto osou, zatiaľ čo zostávajúce sú nad nimi.

[TOC]

Charakteristiky konštantnej funkcie

Môžeme zhrnúť hlavné charakteristiky konštantnej funkcie nasledovne:

-Jeho graf je vodorovná priamka.

-Má jedinečnú križovatku s osou a, hodnota klimatizovať.

-Je to nepretržité.

-Zvládnutie konštantnej funkcie (sada hodnôt, že X) je sada skutočných čísel R.

-Trasa, rozsah alebo rozpor (sada hodnôt, ktoré premenná berie a) je jednoducho konštanta klimatizovať.

Príklady

Funkcie sú potrebné na vytvorenie väzieb medzi veľkosťami, ktoré sa navzájom nejakým spôsobom závisia. Existujúci vzťah medzi nimi možno matematicky modelovať.

Môže vám slúžiť: Papomudas

To pomáha vytvárať modely pre mnoho situácií a robiť predpovede o ich správaní a vývoji.

Napriek svojej zjavnej jednoduchosti má konštantná funkcia veľa aplikácií. Napríklad, pokiaľ ide o štúdium veľkostí, ktoré zostávajú konštantné v čase alebo aspoň na výrazný čas.

Týmto spôsobom sa veľkosti správajú v situáciách, ako napríklad:

-Ten rýchlosť Plavba automobilu, ktorý sa pohybuje na dlhej priamej diaľnici. Pokiaľ sa nezastaví ani nezrýchľuje, auto nesie rovnomerný priamy pohyb.

Obrázok 2. Ak auto nezastaví ani nezrýchľuje, má rovnomerný priamy pohyb. Zdroj: Pixabay.

-Plne načítaný a odpojený kondenzátor z obvodu, má a bremeno konštantný.

-Nakoniec, parkovacie parkovanie, udržuje a cena konštanta bez ohľadu na to, ako dlho tam parkované auto.

Iný spôsob, ako reprezentovať konštantnú funkciu

Konštantná funkcia je možné striedavo reprezentovať takto:

f (x) = kx⁰

Pretože akákoľvek hodnota X Zvýšenie na 0 dáva v dôsledku toho 1, predchádzajúci výraz sa zredukuje na známe:

f (x) = k

Samozrejme to stáva, pokiaľ je to hodnota klimatizovať sa líši od 0.

Preto je konštantná funkcia klasifikovaná aj ako a polynómová funkcia stupeň 0, pretože exponent premennej X Je to 0.

Vyriešené cvičenia

- Cvičenie 1

Odpovedaj na nasledujúce otázky:

a) Je možné potvrdiť, že čiara daná x = 4 je konštantná funkcia? Dôvod svojej odpovede.

b) môže mať konštantnú funkciu križovatku s osou x?

c) je funkcia f (x) = w konštanta²?

Odpovedať

Tu je graf riadku X = 4:

Môže vám slúžiť: štatistické premenné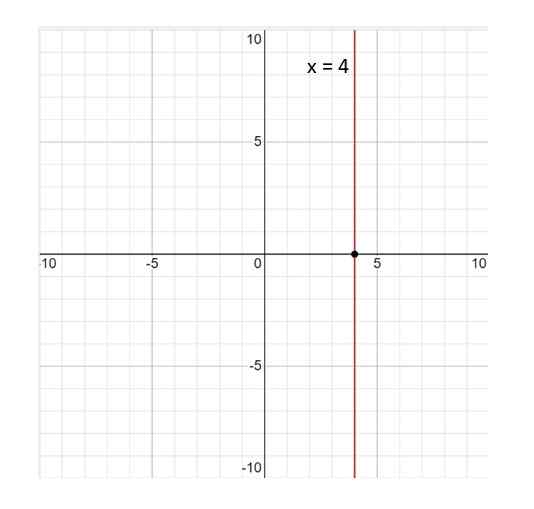 Obrázok 3. Graf riadku X = 4. Zdroj: f. Zapata.

Riadok X = 4 nie je funkcia; Podľa definície je funkcia vzťahom tak, že ku každej hodnote premennej X Zodpovedá jednej hodnote a. A v tomto prípade to nie je splnené, pretože hodnota x = 4 je spojený s nekonečnými hodnotami a. Preto odpoveď je NIE.

Odpoveď B

Všeobecne platí, že konštantná funkcia nemá križovatku s osou X, pokiaľ to nie je y = 0, V takom prípade je to os X Správne povedané.

Odpoveď c

Áno, odvtedy W Je konštantný, jeho štvorec je tiež. Čo je to W Nezávisí to od vstupnej premennej X.

- Cvičenie 2

Nájdite križovatku medzi funkciami f (x) = 5 a G (x) = 5x - 2

Riešenie

Ak chcete nájsť priesečník medzi týmito dvoma funkciami, môžu byť prepísané ako:

y = 5; y = 5x - 2

Sú zladené, získajú:

5x - 2 = 5

Čo je lineárna rovnica prvého stupňa, ktorej riešenie je:

5x = 5+2 = 7

x = 7/5

Bod križovatky je (7/5; 5).

- Cvičenie 3

Demonštrujte, že ten odvodený z konštantnej funkcie je 0.

Riešenie

Z definície derivátu máte:

 f (x) = k

f (x+h) = k

Výmena definície:

Vyššie uvedené dáva zmysel, pretože derivát funkcie je definovaný ako sklon čiary dotyčnej krivke v danom bode. Konštantná funkcia má nulovú čakajúcu a akúkoľvek dotyčničnú čiaru.

Okrem toho, ak uvažujeme o deriváte ako o výmennom kurze Dym/dx, Konštantná funkcia nezažíva žiadnu zmenu, preto je jej derivát neplatný.

Môže vám slúžiť: Multiplikatívny princíp: Techniky počítania a príklady

- Cvičenie 4

Nájsť neurčitú integrál f (x) = k.

Riešenie

- Cvičenie 5

Spoločnosť mobilných telefónov ponúka neobmedzenú internetovú službu s paušálnou sadzbou, ktorá platí 15 dolárov mesačne. Aká je cenová funkcia podľa času?

Riešenie

Nech P je cena, ktorá sa má vyplatiť za $ a t čas, ktorý je možné vyjadriť v dňoch. Funkcia je stanovená nasledovne:

P (t) = 15

- Cvičenie 6

Nasledujúci verzus časový graf zodpovedá pohybu častice.

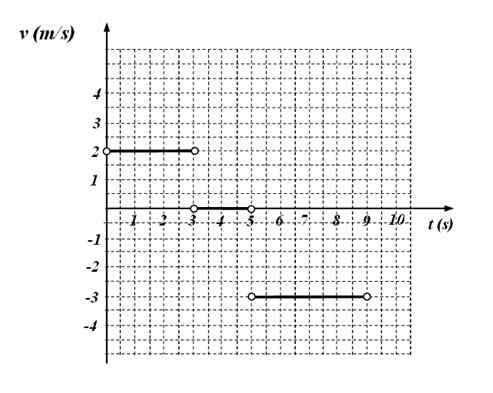Obrázok 4. Funkcia V (t) Funkčný graf pre cvičenie 6. Zdroj: f. Zapata.

Požaduje sa:

a) Napíšte výraz pre rýchlosť funkcie ako funkcia času V (t).

b) Nájdite vzdialenosť prejdená mobilom v časovom intervale medzi 0 a 9 sekundami.

Roztok

Grafu, ktorý to ukazuje:

-V = 2 m/s V časovom intervale medzi 0 a 3 sekundami

-Mobil je zadržaný medzi 3 a 5 sekundami, pretože v tomto intervale je rýchlosť hodnota 0.

-V = - 3 m/s Medzi 5 a 9 sekundami.

Je to príklad kusu kusov alebo funkcie v častiach, ktoré sú zase zložené z konštantných funkcií, ktoré platia iba pre uvedené časové intervaly. Dospelo sa k záveru, že vyhľadávanou funkciou je:

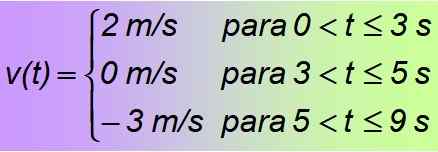
Riešenie B

Z grafu v (t) je možné vypočítať vzdialenosť prevezená mobilom, čo sa číselne rovná oblasti nízkej/na krivke. Tadiaľto:

-Vzdialenosť prešla medzi 0 a 3 sekundami = 2 m/s . 3 s = 6 m

-Medzi 3 a 5 sekundami bol zadržaný, preto necestoval žiadnu vzdialenosť.

-Vzdialenosť prešla medzi 5 a 9 sekundami = 3 m/s . 4 s = 12 m

Celkovo mobilný prešiel 18 m. Vidíte, že hoci je rýchlosť v intervale negatívna medzi 5 a 9 sekundami, prejdená vzdialenosť je pozitívna. Čo sa stane, že v tomto časovom intervale mobil zmenil význam svojej rýchlosti.

Odkazy

1. Geogebra. Konštantné funkcie. Získané z: Geogebra.orgán.
2. Materský. Konštantná funkcia. Obnovené z: Maplesoft.com.
3. Wikilibros. Výpočet vo funkcii premennej/funkcií/konštantnej funkcie. Obnovené z: je.Wikibooks.orgán.
4. Wikipedia. Konštantná funkcia. Zdroj: In.Wikipedia.orgán
5. Wikipedia. Konštantná funkcia. Obnovené z: je.Wikipedia.orgán.