Elastická sila, čo pozostáva, vzorce a cvičenia

Ten elastická sila Je to sila, ktorú objekt vyvíja, aby odolal zmene svojej formy. Prejavuje sa v objekte, ktorý má tendenciu obnovovať svoju formu, keď je pod pôsobením deformačnej sily.

Elastická sila sa tiež nazýva restoratívna sila, pretože je proti deformácii, aby vrátila objekty do svojej rovnovážnej polohy. Prenos elastickej sily je cez častice, ktoré integrujú objekty.

Elastická sila jari

Napríklad, keď je stlačená kovová pružina, sila, ktorá tlačí pružinové častice, sa vyvíja znížením oddelenia medzi nimi, súčasne sa častice odolávajú tlakom, ktoré vyvíjajú silu v rozpore s kompresiou.

Ak namiesto komprimovania pružiny sa vyhodí, napína sa, častice, ktoré ju integrujú. Podobne častice odolávajú oddeleniu sily v rozpore s natiahnutím.

Objekty, ktoré majú vlastnosť obnovenia svojej pôvodnej podoby protichodnou deformačnou silou, sa nazývajú elastické objekty. Springs, elastické gumy a elastické reťazce sú príkladmi elastických predmetov.

[TOC]

Aká je elastická sila?

Elastická sila (F_{klimatizovať}) Je to sila, že objekt uplatňuje obnovenie svojho stavu prírodnej rovnováhy tým, že bol ovplyvnený vonkajšou silou.

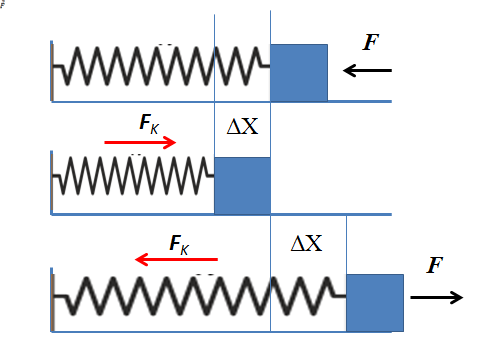
Aby sa analyzovala elastická sila, bude sa brať do úvahy ideálny systém jarnej hmotnosti, ktorý pozostáva z horizontálne umiestnenej pružiny, ktorá je predmetom jedného konca na stene a na druhom konci bloku opovrhnutej hmoty. Ostatné sily pôsobiace na systém, ako je trenie alebo gravitačná sila.

Môže vám slúžiť: Druhá rovnovážna podmienka: Vysvetlenie, príklady, cvičenia

Ak sa na cesto uplatňuje vodorovná sila. Pružina sa pohybuje z rovnovážnej polohy k novej polohe. Pretože objekt má tendenciu zostať v rovnováhe, elastická sila sa prejavuje na pružine, ktorá je proti použitej sile.

Posun naznačuje, do akej miery bola deformovaná pružina a elastická sila, je úmerná tomuto posunu. Keď je pružina stlačená, variácia v polohe sa zvyšuje a následne zvyšuje elastickú silu.

Čím viac je pružina stlačená, tým viac opozičnej sily pôsobí, až kým nedosiahne bod, v ktorom je aplikovaná sila a elastická sila vyvážená, a preto sa systém jarnej hmotnosti prestane pohybovať. Zastavením použitia pevnosti jedinou silou pôsobiacou silou je elastická sila. Táto sila zrýchľuje pružinu v smere v rozpore s deformáciou až do obnovenia stavu rovnováhy.

Rovnakým spôsobom sa vyskytuje pri natiahnutí jar. Pružina je natiahnutá a okamžite uplatňuje silu úmernú k posunu proti protivnému napínaniu.

Vzorce

Vzorec elastickej sily je vyjadrená Hookeovým zákonom. Tento zákon uvádza, že lineárna elastická sila vyvíjaná objektom je úmerná posunu.

F_{klimatizovať} = -K.Δsiež         [1]

F_{klimatizovať} = Elastická sila

klimatizovať = Konštantná proporcionalita

Δsiež = Posun

Keď sa objekt pohybuje vodorovne, rovnako ako v prípade pružiny podliehajúce stene, posun je ΔX, A vyjadrenie Hookeovho zákona je napísané:

F_{klimatizovať} = -K.ΔX        [2]

Môže vám slúžiť: Konvergentná šošovka: Charakteristiky, typy a vyriešené cvičenie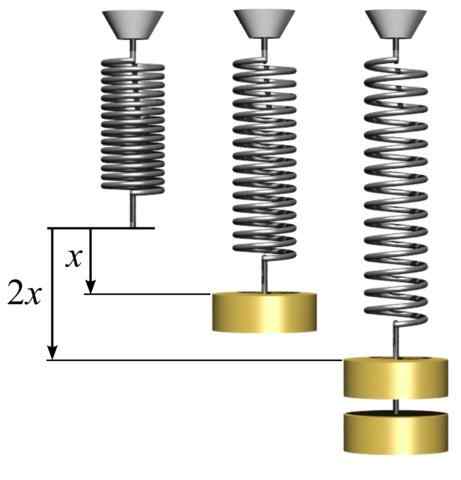Hookeov zákon. Elastická sila úmerná na napínanie. [Svjo (https: // commons.Wikimedia.org/wiki/súbor: Hookes-Law-Prings.Png)]

Záporné znamenie v rovnici naznačuje, že elastická sila pružiny je v opačnom smere ako sila, ktorá spôsobila posun. Konštantná proporcionalita klimatizovať Je to konštanta, ktorá závisí od typu materiálu, ku ktorému je pružina vytvorená. Jednota konštanty klimatizovať je N/m.

Elastické objekty majú limit elasticity, ktorá bude závisieť od konštanty deformácie. Ak sa tiahne za elastický limit, bude sa natrvalo deformovať.

Rovnica [1] a [2] sa vzťahuje na malé pružinové posuny. Ak sú posuny väčšie, pridávajú sa výrazy s väčšou silou ΔX.

Kinetická energia a potenciálna energia označovaná na elastickú silu

Elastická sila funguje na jar posunutím smerom k rovnovážnej polohe. Počas tohto procesu sa zvyšuje potenciálna energia systému jarnej hmotnosti. Potenciálna energia v dôsledku práce vykonanej elastickou silou je vyjadrená v rovnici [3].

U = ½ k .  Δx²[3]

Potenciálna energia je vyjadrená v joules (j).

Zastavením deformačnej sily sa pružina zrýchľuje na rovnovážnu polohu znížením potenciálnej energie a zvýšením kinetickej energie.

Kinetická energia systému pružiny, keď sa rovnovážna poloha dosiahne, je určená rovnicou [4].

A_{klimatizovať}= ½ m.vložka²[4]

m = hmotnosť

vložka = Rýchlosť pružiny

Na vyriešenie jarného hmotnostného systému sa uplatňuje druhý zákon Newtona, berúc do úvahy, že elastická sila je variabilná sila.

Praktické cvičenia príkladov

Získanie deformačnej sily

Koľko sily je potrebná na aplikovanie na pružinu na roztiahnutie 5 cm, ak je pružina konštanta 35n/m?

Môže vám slúžiť: Zrýchlenie gravitácie: Čo je to, ako sa meralo a cvičenia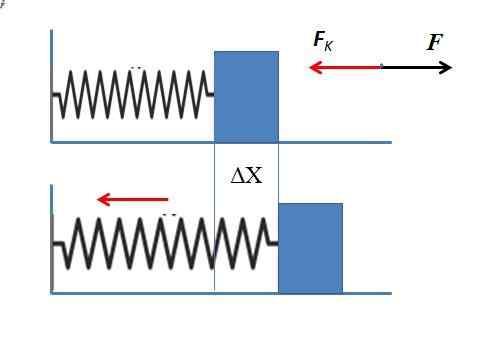Elastická sila pružiny, ktorá sa tiahne 5 cm

Pretože je určená sila aplikácie proti elastickej sile F_{klimatizovať} za predpokladu, že pružina je natiahnutá vodorovne. Výsledok nevyžaduje záporné znamienko, pretože je potrebná sila žiadosti iba.

Hookeov zákon

F_{klimatizovať} = -K.Δx       

Konštanta klimatizovať jar je 35n/m.

Δx = 5 cm = 0,05 m

F_{klimatizovať} = -35n/m . 0,05 m

F_{klimatizovať} = - 1,75n = - f

Potrebný 1,75 n sily deformovať pružinu 5 cm.

Získanie deformačnej konštanty

Aká je deformačná konštanta pružiny, ktorá sa tiahne 20 cm činom sily 60n?

Δx =20 cm = 0,2 m

F = 60n

F_{klimatizovať} = -60n = - f

K = - f_{klimatizovať} / Δx

  = -(-60n)/0,2 m

K = 300 N/m

Jarná konštanta je 300N/m

Získanie potenciálnej energie

Aká je potenciálna energia odvolaná na prácu vykonanú pružnou silou pružiny, ktorá je stlačená 10 cm A jeho deformačná konštanta je 20n/m?

ΔX =10 cm = 0,1 m

K = 20 N/m

F_{klimatizovať} = -20N/m . 0,1 m

F_{klimatizovať} = -200N

Elastická sila jari je -200n.

Táto sila pracuje na jar, aby ju posunula smerom k rovnovážnej polohe. Pri vykonávaní tejto práce sa zvyšuje potenciálna energia systému.

Potenciálna energia sa počíta s rovnicou [3]

U = ½ k .  Δx²

U = ½ (20n/m) . (0,1 m)²

U = 0,1oules

Odkazy

1. Kittel, C, Knight, W D a Ruderman, m a. Mechanika. USA: Mc Graw Hill, 1973, zv. Jo.
2. Rama Reddy, K, Badami, S B a Balasubramanian, V. Oscilamenty a vlny. India: University Press, 1994.
3. Murphy, J. Fyzika: Podporovanie vlastností hmoty a energie. New York: Britannica Educational Publishing, 2015.
4. Giordano, N J. Fyzika vysokej školy: uvažovanie a vzťahy. Kanada: Brooks/Cole, 2009.
5. Walker, J, Halliday, D a Resnick, R. Základy fyziky. USA: Wiley, 2014.