Dynamický alebo kinetický koeficient trenia, príklady, cvičenia

Ten Dynamické trenie alebo kinetický Je to ten, ktorý sa vyskytuje medzi dvoma telami v kontakte, keď sa povrch jedného z nich pohybuje vzhľadom na povrch druhej. Napríklad v krabici, ktorý posúva trenie na svahu, je dynamický a distribuovaný na kontaktnom povrchu bloku.

Sklon musí byť dostatočne veľký, takže tangenciálna zložka hmotnosti sa rovná alebo prekonáva trecia sila, inak by blok, ktorý zostupuje, skončí zastavením.

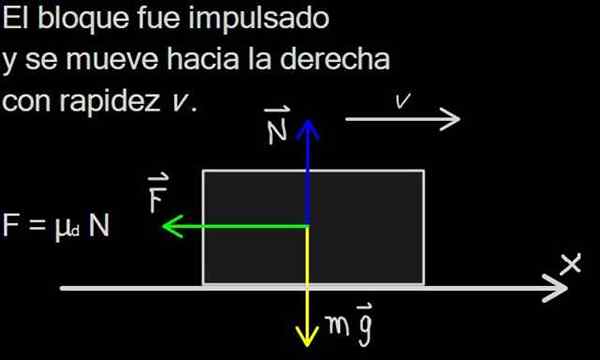
postava 1. Trečná sila je distribuovaná na kontaktnom povrchu bloku, ale v diagrame sily je znázornená ako jedna sila f, zdroj: f. Zapata

Trecia sila má v každodennom živote mimoriadny význam, pretože umožňuje lokomóciu ľudí, zvierat a vozidiel. Na povrchu bez trenia, ako je napríklad zmrzlina, nie je možné začať pohyb.

Trenie tiež umožňuje našim autám zastaviť sa, keď sa pohybujú.

Pri nanášaní brzdy sú brzdové doštičky utiahnuté na disky kolies a vďaka dynamickému treniu zastavte ich rotáciu. Ale nestačí mať dobré brzdy, je potrebné, aby medzi pneumatikami a podlahou bola dostatok trenia, pretože to je nakoniec sila, od ktorej závisí, aby sa auto zastavilo.

Ľudstvo sa naučilo zvládnuť trenie pre svoj prospech. Začalo sa tak pomocou trenia medzi dvoma kusmi suchého dreva na oheň.

Príroda sa tiež naučila zvládnuť trenie v jeho prospech. Napríklad synoviálne membrány, ktoré pokrývajú kosti kĺbov, sú jedným z povrchov s najnižším koeficientom trenia, ktoré existujú.

[TOC]

Koeficient

Prvým, ktorý systematicky študoval pohyb bloku, ktorý sa posúva po rovnom povrchu, bol Leonardo da Vinci, ale jeho štúdie zostali bez povšimnutia.

Môže vám slúžiť: Dirac Jordan Atomic Model: Charakteristiky a postuláty

Až v sedemnástom storočí francúzsky fyzik Guillaume Amontons znovu objavil zákony trenia:

Zákony o dynamickom trení

1.- Trecia sila prítomná v bloku, ktorý sa posúva na rovnom povrchu, vždy proti smeru pohybu.

2.- Rozsah dynamickej trecej sily je úmerný normálnej tesnosti alebo sile medzi povrchmi bloku a podpornou rovinou.

3.- Proporcionálna konštanta je koeficient trenia, statický μ_a V prípade, že nemám sklz a dynamický μ_d Keď existuje. Koeficient trenia závisí od materiálov povrchov v kontakte a stavu drsnosti.

4.- Trecia sila je nezávislá od zjavnej kontaktnej oblasti.

5.- Akonáhle sa pohyb jedného povrchu začína vzhľadom na druhý, trecia sila je konštantná a nezávisí od relatívnej rýchlosti medzi povrchmi.

V tomto prípade nie je kĺzanie, statické trenie sa uplatňuje, ktorého sila je menšia alebo rovná statickému koeficientu trenia vynásobeného normálnym.

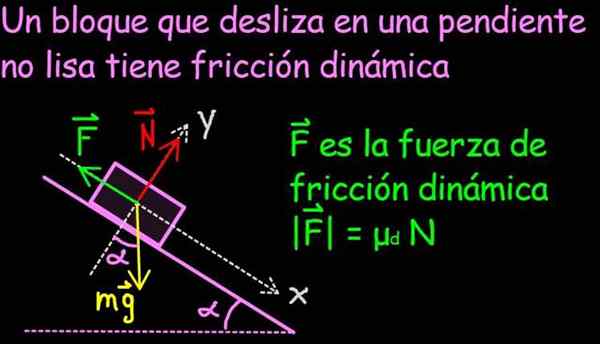
Obrázok 2. Dynamická trecia sila je proti smeru pohybu a jeho veľkosť je úmerná smerom normálnej sily. Konštanta proporcionality je dynamický koeficient trenia. Zdroj: f. Zapata.

Posledný majetok bol výsledkom prínosu francúzskeho fyzika Charlesa Augustina z Coulomb, ktorý je známy pre jeho slávny zákon o sile medzi konkrétnymi elektrickými poplatkami.

Tieto pozorovania nás vedú k matematickému modelu pre dynamickú trennú silu F:

F = μ_d N

Kde μ_d Je to dynamický koeficient trenia a N je normálna sila.

Ako určiť koeficient dynamického trenia?

Experimentálne je stanovený dynamický koeficient trenia medzi dvoma povrchmi. Jeho hodnota závisí nielen od materiálov na oboch povrchoch, ale od stavu drsnosti alebo leštenia, ktoré majú, ako aj od jeho čistoty.

Môže vám slúžiť: Mechanické vlny: Charakteristiky, vlastnosti, vzorce, typy

Jedným zo spôsobov, ako to určiť, je posilniť a posunúť známu box na vodorovnom povrchu.

Ak je rýchlosť známa v čase poháňania a meria sa vzdialenosť od tej doby, je možné poznať zrýchlenie brzdenia v dôsledku dynamického trenia.

Experimentovať 

V tomto experimente sa merala počiatočná rýchlosť vložka a vzdialenosť d, Takže brzdové zrýchlenie je:

A = - v² / 2d

Schéma síl je znázornená na obrázku 2. Veľkosť hmotnosti je hmotnosť m bloku vynásobená zrýchlením gravitácie g, a ako je známe, hmotnosť vždy smeruje vertikálne nadol.

N Je to normálna sila v dôsledku ťahu na podpornej ploche a je vždy kolmá (alebo normálna) do roviny. Normálne existuje, keď sú povrchy v kontakte a prestanú, len čo sa povrchy oddelia.

Sila F predstavuje dynamickú trennú silu. V skutočnosti je distribuovaný na spodnom povrchu bloku, ale môžeme ho reprezentovať ako jediná sila F aplikované v strede bloku.

Pretože existuje vertikálna rovnováha, veľkosť normálu N Rovná sa s hmotnosťou mg:

N = mg

V horizontálnom smere trecia sila vytvára spomalenie hmotnostného bloku M podľa druhého zákona Newtona:

-F = m a

Trecia sila F body vľavo, takže jeho horizontálna zložka je záporná, m je hmotnosť bloku a A je brzdné zrýchlenie.

Predtým získal A = - v² / 2d A tiež dynamický model trenia naznačuje, že:

F = μd n

Výmena v predchádzajúcej rovnici, ktorú máte:

-μ_d N = - vložka² / 2d

Berúc do úvahy, že n = mg už môžete vyčistiť dynamický koeficient trenia: 

Môže vám slúžiť: Schrödinger Atomický model

μ_d = vložka² / (2d mg)

Rocy koeficient tabuľky niektorých materiálov

Nasledujúca tabuľka ukazuje statické a dynamické koeficienty trenia pre rôzne materiály. Je potrebné poznamenať, že systematicky je koeficient statického trenia vždy väčší ako koeficient dynamického trenia.

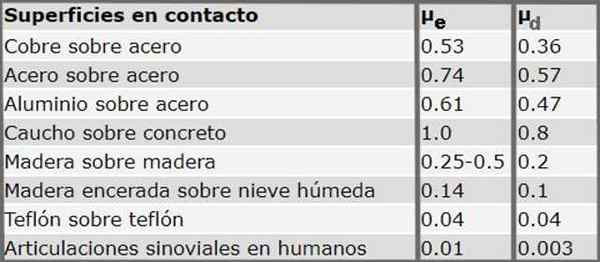Obrázok 3. Statické a dynamické koeficienty trenia pre niekoľko povrchov v kontakte. Zdroj: Serway r.Do. Fyzický. McGraw-Hill (1992)

Cvičenia

- Cvičenie 1

Propaguje sa 2 kg blok cesta na vodorovnej podlahe a uvoľňuje sa. V čase uvoľnenia sa zaznamená rýchlosť 1,5 m/s. Od tej chvíle, kým sa blok nezastaví dynamickým trením 3 m. Stanovte koeficient kinetického trenia.

Riešenie

Podľa vzorca získaného v príklade predchádzajúcej časti je dynamický (alebo kinetický) koeficient::

μ_d = vložka² / (2d mg) = 1.52 / (2x3x2 x9,8) = 0,019.

- Cvičenie 2

S vedomím, že blok na obrázku 1 zostupuje konštantnou rýchlosťou, že hmotnosť bloku je 1 kg a že sklon roviny je 30 °, určuje:

a) Hodnota dynamického trenia

b) Dynamický koeficient trenia medzi blokom a rovinou.

Riešenie

Na obrázku 4 je hnutia rovnica (druhý zákon Newtonu) znázornené pre problém bloku, ktorý zostupuje sklon s koeficientom trenia μ_d  a a sklon (pozri schému síl na obrázku 1)

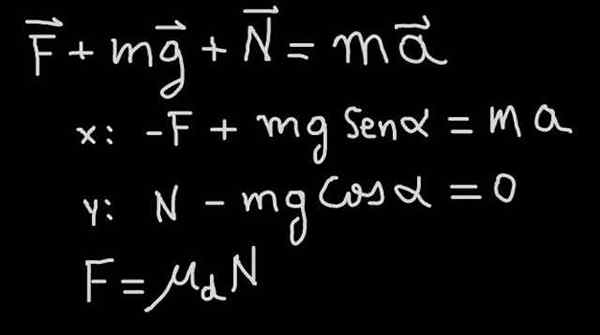Obrázok 4. Newtonov druhý zákon sa vzťahoval na blok, ktorý sa posúva na svahu s trením. Zdroj: f. Zapata.

V našom cvičení sa hovorí, že blok zostupuje konštantnou rýchlosťou, preto zostupuje s zrýchlením A = 0. Z toho vyplýva, že trecia sila je taká, že sa rovná tangenciálnej zložke hmotnosti: f = mg sen (α).

V našom prípade m = 1 kg a a = 30 °, takže trecia sila f má hodnotu 4,9n.

Na druhej strane, normálna sila n je rovnaká a na rozdiel od kolmej zložky hmotnosti: n = mg cos (a) = 8,48n .

Z toho vyplýva, že koeficient dynamického trenia je:

μ_d = F / n = 4,9n / 8,48n = 0,57

Odkazy

1. Alons m., Finn e. 1970. Fyzický. Zväzok I. Mechanika. Inter -American Educational Fund S.Do.
2. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
3. Hewitt, P. 2012. Koncepčná fyzická veda. Piaty vydanie.
4. Rex, a. 2011. Základy fyziky. Pearson. 
5. Serway R. 1992. Fyzický. McGraw-Hill.
6. Mladý, h. 2015. Fyzika univerzity s modernou fyzikou. 14. vydanie. Pearson.