Frakcie rovnajúce sa 3/4

Ten Frakcie rovnajúce sa 3/4 Sú to tí, v ktorých vydelením čitateľa medzi menovateľ vedie k desatinnému číslu 0.75.

Je to vždy možné. Ak sa výsledok tejto operácie rovná 0.75, frakcia je rovnocenná 3/4, napríklad zlomok 6/8:

Frakcia 6/8 je rovnocenná s ¾, pretože rozdelením čitateľa medzi menovateľ sa v oboch prípadoch 0 získa 0.75. Zdroj: f. Zapata.

Teraz sa frakcia 6/8 získala vynásobením čitateľa aj menovateľa ¾. Súčasným vynásobením čitateľa a menovateľa rovnakým množstvom sa desatinná hodnota danej frakcie nezmení, ale umožňuje získať frakcie, ktoré sú rovnocenné s daným.

Ďalším spôsobom, ako nájsť frakciu ekvivalentnú inej. V prípade ¾ však nie je možné nájsť také číslo, ktoré sa delí súčasne na 3 a 4 a výsledkom je celé číslo. Je to preto, že 3 a 4 sú navzájom bratranci, takže nemajú spoločných deliacich.

Keď čitateľ a menovateľ frakcie sú navzájom hlavnými číslami, hovorí sa, že frakcia je neredukovateľný. Preto je ¾ neredukovateľný.

Spôsoby, ako nájsť zlomok ekvivalentný inému

Existujú dva veľmi jednoduché spôsoby, ako nájsť frakčný ekvivalent k inej danej frakcii: prvý je redukcia a druhá zosilnením.

Redukcia a zosilnenie frakcií

Zníženie

Tento postup spočíva v nájdení čísla, ktoré je deliteľom čitateľa aj menovateľa. Po nájdení sú čitateľ aj menovateľ vydelený touto hodnotou a okamžite získal frakciu ekvivalentnú originálu. Overí sa, že to robí pomer čitateľa medzi menovateľom a porovnaním.

Môže vám slúžiť: matematické funkcie

Keď je neredukovateľný zlomok iného. Takto získaná frakcia je neredukovateľná.

Frakcia ¾ je neredukovateľná, ako už bolo uvedené, pre seba, pretože sú navzájom 3 a 4 bratrancami, ale nasledujúca metóda umožňuje nekonečné frakcie rovnocenné s ¾.

Zosilnenie

Na zosilnenie danej frakcie sa musí čitateľ a menovateľ vynásobiť rovnakou sumou, bez ohľadu na to, či ide o kladné alebo záporné číslo. Napríklad frakcia 6/8 bola získaná zosilnením ¾ faktorom 2:

Aj keď frakcie majú iného čitateľa a menovateľa, obe sú rovnaké.

Všimnite si nasledujúci obrázok, ktorý obsahuje dva rovnaké kruhy, ktoré sú rozdelené do rovnakých častí, hoci rôzni veľkosť. Opatrne pozorovanie, oblasti v zelenej a fialovej farbe majú rovnaké opatrenie, ale zelená oblasť bola rozdelená na 3 časti, z celkového počtu 4, ktoré tvoria kruh vľavo. Na druhej strane, kruh doprava bol rozdelený na 8 rovnakých častí a fialová oblasť je rovnocenná 6 z nich.

Týmto spôsobom môžete grafovať, že ¾ je ekvivalent 6/8, pretože obe frakcie predstavujú rovnakú sumu.

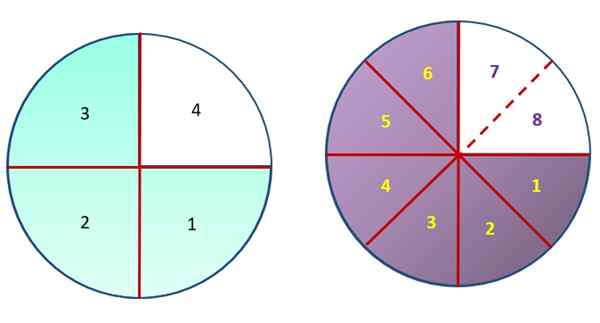Frakcie ¾ a 6/8 predstavujú rovnakú oblasť v oboch kruhoch. Zdroj: f. Zapata.

Všeobecne platí, že ak sa frakcia vynásobí ¾ podľa čísla n, toľko frakcií, ktoré sa rovnajú, sa získa tak, ako chcete:

Je dôležité poznamenať, že n sa nikdy nemôže rovnať 0, pretože delenie 0 nie je definované. Žiadny zlomok nemôže mať vo vašom menovateľovi 0.

Ako zistiť, či je zlomok rovnocenný s 3/4?

Ako je vysvetlené na začiatku, spôsob, ako zistiť, či je frakcia rovnocenná s ¾, je urobiť kvocient medzi čitateľom a menovateľom. Ak je 0.75, frakcia je rovnocenná s ¾, ale existuje niekoľko ďalších metód, ktoré treba poznať, ktoré nevyžadujú priame rozdelenie:

Môže vám slúžiť: vážené médiá: Ako sa vypočítajú, príklady a cvičenia

Spôsob 1

Predpokladajme, že frakcia A/B, a chcete vedieť, či je rovnocenná s ¾, to znamená, ak je pravda, že:

Aby bol produkt 4 rovnocenný, musí sa rovnať produktu 3B:

4a = 3B

Metóda 2

Ak je frakcia A/B rovnocenná s ¾, čo vydelí A a B maximálnym spoločným deliteľom MCD, výsledok musí byť ¾.

Ak chcete objasniť použitie týchto metód, pozri nasledujúce príklady.

Príklady

Príklad 1

Určite, či frakcia 150/200 je rovnocenná s ¾:

Metódou 1

V tomto prípade a = 150 a b = 200, musí sa splniť, že:

4a = 3B

• 4 × 150 = 600
• 3 × 200 = 600

Dospelo sa k záveru, že 150/2 200 je rovnocenné s ¾.

Metódou 2

Maximálny spoločný deliteľ 150 a 300 ich rozdelí presne. Obe množstvá sa rozkladajú vo svojich hlavných faktoroch a potom sa vynásobia spoločné faktory s ich najmenším exponentom:

• 150 = 2 × 5² × 3
• 200 = 2³ × 5²

2 a 5 sú bežné, vynásobia výber najmenšej sily, s akou sa objavujú:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Teraz pokračujeme v rozdelení:

Vyriešené cvičenia

Cvičenie 1

Napíšte amplifikáciou päť frakcií rovnajúcich sa ¾, vynásobenie čitateľa a menovateľa zakaždým podľa nasledujúcich celých čísel:

a) 3, b) 5, c) (-2), d) 10 a e) 20

Roztok

Riešenie B

Riešenie c

Všimnite si, že nie je rozdiel tým, že zosilnenie frakcie o 2 alebo -2.

Riešenie d

Riešenie e

Všimnite si, že táto frakcia je rovnaká ako získaná amplifikáciou 2 Frakcia získaná vyššie:

Cvičenie 2

Overte, či sú tieto frakcie rovnocenné s ¾:

Môže vám slúžiť: obdĺžnikové súradnice: príklady a cvičenia vyriešené

A) 18/24; b) 21/28; c) 24/32; d) 27/38; e) 33/44

Roztok

Použitie metódy 1 opísanej vyššie:

4a = 3B

Pre zlomok 18/24 musíte = 18 a b = 24, potom:

• 4 × 18 = 72
• 3 × 24 = 72

Preto sú 18/24 a 3/4 rovnocenné.

Riešenie B

Podľa metódy 2 musíme nájsť maximálny spoločný deliteľ (MCD) 21 a 28, potom rozdeliť výsledok, a ak sa získa frakcia 3/4, sú rovnocenné:

21 = 3 × 7
28 = 4 × 7 = 2²× 7

Spoločným faktorom je 7, preto MCD (21,28) = 7, potom:

Riešenie c

Pre toto cvičenie sa skontroluje, či kvocient medzi 24 a 32 je 0 0.75:

24 ÷ 32 = 0.75

Potom je 24/32 ekvivalent 3/4.

Riešenie d

Vo frakcii 27/38 sa pozoruje, že 38 nie je násobok 4, preto to nie je rovnocenné 3/4. V každom prípade sa vykonáva pomer medzi 27 a 38:

27 ÷ 38 = 0.710526

Z ktorých sa dospelo k záveru, že 27/38 nie je rovnocenné 3/4.

Riešenie e

Je ľahké vidieť, že frakcia 33/44 sa získa vynásobením čitateľa a menovateľa 3/4 x 11, ako je tento:

Preto sú rovnocenné.