Faktor stlačiteľnosti Ako vypočítať, príklady a cvičenia

On Faktor stlačiteľnosti Z, o Kompresný faktor pre plyny, je bezrozmerná hodnota (bez jednotiek), ktorá sa zavádza ako korekcia v stavom rovnici ideálnych plynov. Týmto spôsobom matematický model pripomína pozorované správanie plynu viac.

V ideálnom plyne je štátna rovnica, ktorá sa týka premenných p (tlak), v (objem) a t (teplota): P.Vložka _ideálny = n.R.Tón s n = počet krtkov a r = konštanta ideálnych plynov. Pridanie korekcie kompresívneho faktora Z sa táto rovnica transformuje na:

P.V = z.n.R.Tón

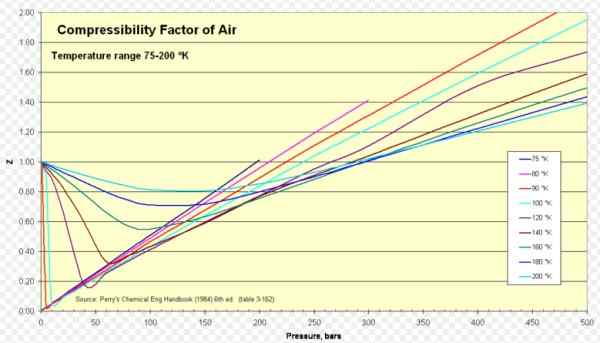
postava 1. Faktor stlačiteľnosti vzduchu. Zdroj: Wikimedia Commons. https: // nahrávanie.Wikimedia.org/wikipedia/commons/8/84/compressibility_factor_of_air_75-200_k.Png.

[TOC]

Ako vypočítať faktor stlačiteľnosti?

Berúc do úvahy, že molárny objem je Vložka_ochladiť = V/n, Máte skutočný molárny objem:

P . Vložka_reálny = Z. R. T → z = PV _reálny/Rt

Pretože faktor stlačiteľnosti Z závisí od podmienok plynu, vyjadruje sa ako funkcia tlaku a teploty:

Z = z (p, t)

Pri porovnaní prvých dvoch rovníc sa uvádza, že ak sa počet mólov n rovná 1, molárny objem skutočného plynu súvisí s objemom ideálneho plynu cez:

Vložka_reálny / V_ideálny = Z → V _reálny = Z V_ideálny

Keď tlak presahuje 3 atmosféry, väčšina plynov sa prestane správať ako ideálne plyny a skutočný objem sa výrazne líši od ideálneho.

To sa uskutočnilo vo svojich experimentoch Holandský fyzik Johannes van der Waals (1837-1923), čo ho viedlo k vytvoreniu modelu, ktorý sa lepšie prispôsobil praktickým výsledkom ako rovnica ideálnych plynov: štátna rovnica Van der Waals.

Môže vám slúžiť: oxalát sodný (Na2C2O4): Štruktúra, vlastnosti, použitia, riziká

Príklady

Podľa rovnice P.Vložka_reálny= Z.n.Rt, Pre ideálny plyn, z = 1. Avšak v skutočných plynoch zvyšuje tlak aj hodnota Z. To dáva zmysel, pretože pri väčších tlakových molekulách plynu majú viac príležitostí na zrážanie, preto sa odpudivé sily zvyšujú, a tým objem.

Na druhej strane do nižších tlakov sa molekuly pohybujú s väčšou voľnosťou a odpudivé sily klesajú. Preto sa očakáva nižší objem. Pokiaľ ide o teplotu, keď sa zvyšuje, Z klesá.

Ako poznamenal Van der Waals, v blízkosti takzvaného kritického bodu je správanie plynu veľmi odklonené od ideálneho plynu.

Kritický bod (t_c, P_c) akejkoľvek látky sú hodnoty tlaku a teploty, ktoré určujú ich správanie pred zmenou fázy:

-Tón_c Je to teplota nad ktorou nie je daný plyn skvapalnený.

-P_c  Je to minimálny tlak potrebný na skvapalnenie plynu pri teplote t_c

Každý plyn má však svoj vlastný kritický bod, ale definuje teplotu a znížený tlak t_r A p_r nasledovne:

P_r = P / p_c

Vložka_r = V /v_c

Tón_r = T /t_c

Zistilo sa, že plyn obmedzený s identickým Vložka_r a Tón_r vyvíjať rovnaký tlak P_r. Z tohto dôvodu, ak je z grafický v závislosti od P_r to isté Tón_r, Každý bod v tejto krivke je rovnaký pre akýkoľvek plyn. Toto sa volá Zásada zodpovedajúcich štátov.

Faktor stlačiteľnosti v ideálnych plynoch, vzduchu, vodíku a vode

Nižšie je krivka stlačiteľnosti pre rôzne plyny pri rôznych znížených teplotách. Potom niekoľko príkladov z pre niektoré plyny a postup na nájdenie z použitím krivky.

Môže vám slúžiť: Vodík: História, štruktúra, vlastnosti a použitia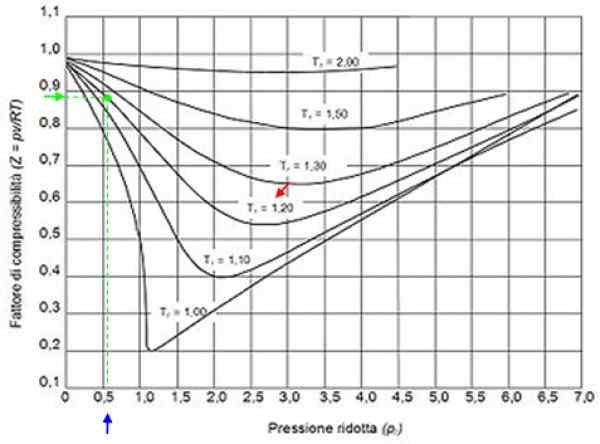Obrázok 2. Grafická grafika pre plyny podľa redukčného tlaku. Zdroj: Wikimedia Commons.

Ideálne plyny

Ideálne plyny majú z = 1, ako je vysvetlené na začiatku.

Vysielať

Pre vzduch z je približne 1 v rozsiahlom rozsahu teploty a tlakov (pozri obrázok 1), kde ideálny model plynu poskytuje veľmi dobré výsledky.

Vodík

Z> 1 pre všetky tlaky.

Vodná voda

Na nájdenie z vody sú potrebné hodnoty kritického bodu. Kritický bod vody je: P_c = 22.09 MPA a T_c= 374.14 ° C (647.3 k). Opäť je potrebné vziať do úvahy, že faktor stlačiteľnosti Z závisí od teploty a tlaku.

Predpokladajme napríklad, že chcete nájsť Z z vody pri 500 ° C a 12 MPa. Potom je prvým výpočtom zníženej teploty, pre ktorú sa musia Celzia stupne odovzdať do Kelvinu: 50 ° C = 773 K:

Tón_r = 773/647.3 = 1.2

P_r = 12/22.09 = 0.54

S týmito hodnotami sa nakladáme v grafe obrázku, krivka zodpovedajúca T_r = 1.2, označené červenou šípkou. Potom sa pozrieme do horizontálnej osi hodnota P_r bližšie k 0.54, označené modrou farbou. Teraz kreslíme zvislú, až kým nezachytíme krivku T_r = 1.2 A nakoniec sa premieta od tohto bodu do vertikálnej osi, kde čítame približnú hodnotu z = 0.89.

Vyriešené cvičenia

Cvičenie 1

Vzorka plynu je pri teplote 350 K a tlak 12 atmosféry, pričom molárny objem o 12 % je vyšší, ako sa predpokladá, že zákon ideálnych plynov. Vypočítať:

A) Z Kompresný faktor.

b) molárny objem plynu.

Môže vám slúžiť: nezvratná reakcia: Charakteristiky a príklady

c) Podľa vyššie uvedených výsledkov naznačte, ktoré sú dominantné sily v tejto vzorke plynu.

Údaje: r = 0,082 l.bankomat/mol.Klimatizovať

Roztok

Vedieť, že v _reálny  je o 12 % vyššia ako Vložka_ideálny :

Vložka_reálny  = 1.12V_ideálny

Z = v _reálny / V_ideálny = 1.12

Riešenie B

P . Vložka_reálny = Z. R. T → V_reálny = (1.12 x 0.082 x 350/12) l /mol = 2.14 l/mol.

Riešenie c

Odpudkové sily sú sily, ktoré prevládajú, pretože objem vzorky sa zvýšil.

Cvičenie 2

Existuje 10 mólov etánu uväznených v objeme 4.86 L A 27 ° C. Nájdite tlak vyvíjaný etánom z:

a) Model ideálneho plynu

b) Van der Waalsova rovnica

c) Nájdite kompresný faktor z predchádzajúcich výsledkov.

Údaje pre etán

Van der Waals koeficienty:

A = 5.489 dm⁶. Bankomat . mol^-2  a b = 0.06380 dm³. mol^-1.

Kritický tlak: 49 bankomat. Kritická teplota: 305 K

Roztok

Teplota sa prenáša na Kelvin: 27 ° C = 27 +273 K = 300 K, nezabudnite tiež, že 1 liter = 1 l = 1 dm³.

Potom sa údaje uvedené v ideálnej plynovej rovnici vymenia:

P.V = n.R.T → p = (10 x 0,082 x 300/4.86 l) bankomat = 50.6 bankomat

Riešenie B

Štátna rovnica van der Waals je:

Kde A a B sú koeficienty uvedené vyhlásením. Pri zúčtovaní p:

Riešenie c

Vypočítame znížený tlak a teplotu:

P_r = 35.2/49 = 0.72

Tón_r = 300/305 = 0.98 ≈ 1

S týmito hodnotami sa hľadá hodnota z v grafe na obrázku 2, zistenie, že Z je približne 0.7.

 Odkazy

1. Atkins, str. 1999. Fyzikálna chémia. Vydanie omega.
2. Cengel a. 2012. Termodynamika. 7^mamička Vydanie. McGraw Hill.
3. Engel, T. 2007. Úvod do fyzikálnej konže: Termodynamika. Pearson.
4. Levine, i. 2014. Princípy fyziky chémie. 6. Vydanie. McGraw Hill.
5. Wikipedia. Faktor stlačiteľnosti. Zdroj: In.Wikipedia.orgán.