Spoločný faktor pre zoskupovanie podmienok príkladov, cvičení

On spoločný faktor pre zoskupovanie podmienok Je to algebraický postup, ktorý umožňuje písanie niektorých algebraických výrazov vo forme faktorov. Na dosiahnutie tohto cieľa musí výraz najprv pohodlne zoskupovať a pozorovať, že každá takto vytvorená skupina má v skutočnosti spoločný faktor.

Správne použitie tejto techniky si vyžaduje určitú prax, ale v krátkom čase je možné dominovať. Pozrime sa najskôr ako ilustratívny príklad opísaný krok za krokom. Potom čitateľ môže uplatniť to, čo sa naučili v každom z cvičení, ktoré sa objavia po.

postava 1. Odstráňte spoločný faktor pre zoskupovanie výrazov uľahčuje prácu s algebraickými výrazmi. Zdroj: Pixabay.

Predpokladajme napríklad, že musíte zohľadniť nasledujúci výraz:

2x² + 2xy - 3ZX - 3Zy

Tento algebraický výraz pozostáva zo 4 monomálov alebo výrazov, oddelených znakmi + a -, konkrétne:

2x², 2xy, -3zx, -3zy

Pozorne pozorne X je spoločné pre prvé tri, ale nie pre posledné, zatiaľ čo a je spoločné pre druhú a štvrtú a Z je spoločné pre tretí a štvrtý.

Takže v zásade neexistuje spoločný faktor pre štyri výrazy súčasne, ale ak sú zoskupené tak, ako sa zobrazia v nasledujúcej časti, môže vám pomôcť napísať výraz ako produkt dvoch alebo viacerých faktorov.

[TOC]

Príklady

Faktor výrazu: 2x² + 2xy - 3ZX - 3Zy

Krok 1: Zoskupenie

2x² + 2xy - 3Zx - 3Zy = (2x² + 2xy) + (-3zx - 3Zy)

Krok 2: Odstráňte spoločný faktor z každej skupiny

2x² + 2xy - 3ZX - 3Zy =

= (2x² + 2xy) - (3ZX + 3zy) =

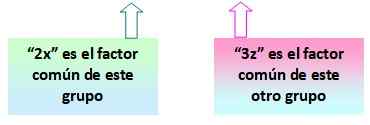
= 2x (x+y) - 3z (x+y)

JoMlčanie: Negatívny znak je tiež spoločným faktorom, ktorý sa musí zohľadniť.

Môže vám slúžiť: Vektorový priestor: základňa a rozmer, axiómy, vlastnosti

Teraz si všimnite, že zátvorka (x+y) sa opakuje v dvoch výrazoch získaných pri zoskupení. To je spoločný faktor, ktorý hľadal.

Krok 3: Faktorizujte všetok výraz

2x² + 2xy - 3ZX - 3Zy = (x+y) (2x - 3z)

S predchádzajúcim výsledkom bol dosiahnutý cieľ faktorizácie, ktorý nie je ničím iným ako transformácia algebraického výrazu na základe súm a odčítania výrazov v produkte dvoch alebo viacerých faktorov, v našom príklade: (x+ y) a (2x - 3z).

Dôležité otázky týkajúce sa spoločného skupinového faktora

Otázka 1: Ako zistiť, že výsledok je správny?

Odpoveď: Distribučná vlastnosť sa aplikuje na získaný výsledok a po znížení a zjednodunutí sa takto dosiahnutý výraz musí zhodovať s originálom, ak nie, existuje chyba.

V predchádzajúcom príklade funguje spätne s výsledkom, aby sa overil, či je v poriadku:

(x+y) (2x - 3z) = 2x² -3ZX +2xy - 3zy

Pretože poradie dodatkov nezmení sumu, po uplatňovaní distribučnej vlastnosti, všetky pôvodné výrazy existujú, sú preto zahrnuté znaky, faktorizácia je preto správna.

Otázka 2: Mohli ste zoskupovať iným spôsobom?

Odpoveď: Existujú algebraické výrazy, ktoré pripúšťajú viac ako jednu formu zoskupenia a ďalšie, ktoré nie sú. Vo vybranom príklade môže čitateľ vyskúšať ďalšie možnosti, napríklad zoskupenie:

2x² + 2xy - 3Zx - 3Zy = (2x²- 3ZX) + (2xy - 3Zy)

A vidíte, že výsledok je rovnaký ako tu získaný. Nájdenie optimálnej skupiny je záležitosťou praxe.

Môže vám slúžiť: Cotangent odvodené: výpočet, demonštrácia, cvičenia

Otázka 3: Prečo je potrebné získať spoločný faktor z algebraického výrazu?

Odpoveď: Pretože existujú aplikácie, v ktorých faktorizovaný výraz uľahčuje výpočty. Predpokladajme napríklad, že chcete urobiť 2x² + 2xy - 3ZX - 3Za rovnajúci sa 0. Aké by boli možnosti?

Na reagovanie na tento problém je faktorizovaná verzia oveľa užitočnejšia ako pôvodný vývoj z hľadiska. Vznikne to takto:

(x+y) (2x - 3z) = 0

Jednou z možností, že výraz má hodnotu 0, je to, že x = -y, bez ohľadu na hodnotu z. A druhým je, že x = (3/2) z, bez záležitostí hodnoty y.

Cvičenia

- Cvičenie 1

Získajte spoločný faktor nasledujúceho výrazu zoskupením výrazov:

AX+AY+BX+

Riešenie

Prvé dva sú zoskupené, so spoločným faktorom „A“ a poslednými dvoma s spoločným faktorom „B“:

AX+AY+BX+BU = A (X+Y)+B (X+Y)

Akonáhle sa to stane, odhaľuje sa nový spoločný faktor, ktorý je (x+y), takže:

AX+AY+BX+BY = A (x+y)+b (x+y) = (x+y) (a+b)

Ďalší spôsob zoskupenia

Tento výraz pripúšťa ďalší spôsob zoskupenia. Pozrime sa, čo sa stane, ak sú podmienky preusporiadané a je vyrobená skupina, s ktorou obsahujú X a ďalšie s tými, ktoré obsahujú a:

AX +AY +BX +BY = AX +BX +AY +BU = X (A +B) +Y (A +B)

Týmto spôsobom je nový spoločný faktor (A+B):

AX+AY+BX+BY = AX+BX+AY+BU = X (a+b)+y (a+b) = (x+y) (a+b)

To vedie k rovnakému výsledku prvého spôsobu zoskupovania, ktorý bol testovaný.

- Cvičenie 2

Ako produkt dva faktory je potrebné napísať nasledujúci algebraický výraz:

Tretí³ - Tretí²B+9AB²-do²+AB-3B²

Môže vám slúžiť: Coplanares body: rovnica, príklad a vyriešené cvičenia

Riešenie

Tento výraz obsahuje 6 výrazov. Skúsme zoskupovať prvé a štvrté, druhé a tretie a konečne piaty a šiesty:

Tretí³ - Tretí²B+9AB²-do²+AB-3B² = (3³ -do²) + (- 3²B+9AB²) + (AB-3B²)

Teraz je každá zátvorka faktorom:

= (3³ -do²) + (- 3²B+9AB²) + (Ab -3b²) = a² (3a -1) + 3ab (3b -a) + b (a -3b)

Na prvý pohľad sa zdá, že situácia bola komplikovaná, ale čitateľ by sa nemal odradiť, pretože sa chystáme prepísať posledný termín:

do² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

Posledné dva termíny majú teraz spoločný faktor, ktorý je (3B-A), takže ich možno faktorizovať. Je veľmi dôležité nestratiť zo zreteľa prvé funkčné obdobie² (3a - 1), čo musí naďalej sprevádzať všetko ako pridávanie, takže s ním nepracujete:

do² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3a-1) + (3B-A) (3AB-B)

Expresia bola znížená na dva termíny a v poslednom z nich sa objaví nový spoločný faktor, ktorý je „B“. Teraz zostáva:

do² (3a-1) + (3b-a) (3ab-b) = a² (3a-1) +b (3b-a) (3a-1)

Ďalším spoločným faktorom, ktorý sa objaví, je 3. - 1:

do² (3a - 1) +b (3b -a) (3a -1) = (3a - 1) [a² + B (3B-A)]

Alebo ak dávate prednosť bez štvorcových držiakov:

(3. - 1) [a² + B (3b -a)] = (3a - 1) (a² -AB + 3B²)

Môže čitateľ nájsť ďalší spôsob zoskupenia, ktorý vedie k rovnakému výsledku?

Obrázok 2. Navrhované faktorizačné cvičenia. Zdroj: f. Zapata.

Odkazy

1. Baldor, a. 1974. Elementárna algebra. Venezuelský kultúrny.Do.
2. Jiménez, r. 2008. Algebra. Sála.
3. Hlavné prípady faktorizácie. Získané z: Julioprofe.slepo.
4. Žobrák. Základná matematika: faktorizácia zoskupením výrazov. Fakulta účtovníctva a správy.
5. Zill, D. 1984. Algebra a trigonometria. Kopec MacGraw.