Existujú Scale -trojuholníky s pravým uhlom?

Existuje veľa trojuholníkov Scale s pravým uhlom. Predtým, ako postupuje na túto tému, je najprv potrebné poznať rôzne typy trojuholníkov, ktoré existujú. Trojuholníky sú klasifikované dvoma triedami, ktoré sú: ich vnútorné uhly a dĺžky ich strán.

Súčet vnútorných uhlov akéhokoľvek trojuholníka sa vždy rovná 180 °. Ale podľa vnútorných opatrení uhlov sú klasifikované ako:

-Akulógový: Tieto trojuholníky sú také, že ich tri uhly sú akútne, to znamená, že merajú menej ako 90 °.

-Obdĺžnik: Sú to tie trojuholníky, ktoré majú pravý uhol, to znamená uhol, ktorý meria 90 °, a preto sú ďalšie dva uhly akútne.

-Tupý: Sú to trojuholníky, ktoré majú tupý uhol, to znamená uhol, ktorého miera je väčšia ako 90 °.

Scalan trojuholníkov s pravým uhlom

Záujem o túto časť je určiť, či môže mať Scalen Triangle pravý uhol.

Ako je uvedené vyššie, pravý uhol je uhol, ktorého miera je 90 °. Je potrebné poznať iba definíciu Scalenovho trojuholníka, ktorý závisí od dĺžky strán trojuholníka.

Klasifikácia trojuholníkov podľa ich strán

Podľa dĺžky ich strán sú trojuholníky klasifikované ako:

-Rovnocenný: Sú to všetky tie trojuholníky tak, že dĺžky ich troch strán sú rovnaké.

-Izoscely: Sú to trojuholníky, ktoré majú presne dve strany rovnakej dĺžky.

-Vyskakovať: Sú to tie trojuholníky, na ktorých majú tri strany rôzne opatrenia.

Formulácia rovnocennej otázky

Otázka, ktorá je rovnajúca sa otázkam názvu, je „Existujú trojuholníky, ktoré majú všetky tri strany s rôznymi opatreniami, a to má uhol 90 °?„

Odpoveď, ako je uvedené na začiatku, je áno. Nie je veľmi ťažké odôvodniť túto odpoveď.

Ak je to starostlivo pozorované, žiadny obdĺžnikový trojuholník nie je rovnocenný, možno to odôvodniť vďaka vete Pythagoras pre trojuholníky obdĺžnikov, ktorá hovorí:

Vzhľadom na obdĺžnikový trojuholník, že dĺžky ich kategórií sú „a“ a „b“ a dĺžka jeho hypotenusu je „c“, musíte c² = a²+b², čo je možné vidieť, že dĺžka hypotenusu “ C “je vždy väčší ako dĺžka každej nohy.

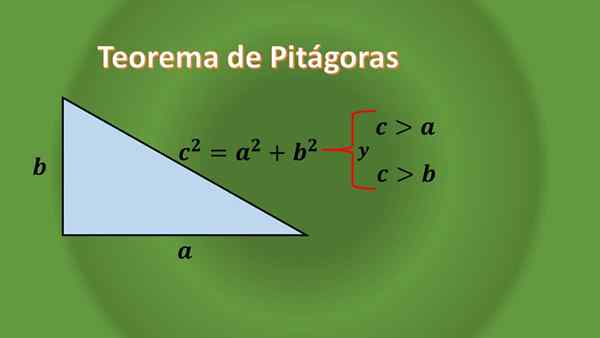
Keďže sa nič nehovorí o „A“ a „B“, potom to znamená, že pravým trojuholníkom môže byť izoscely alebo skláňanie.

Potom si jednoducho vyberte akýkoľvek obdĺžnikový trojuholník tak, aby jeho nohy mali rôzne opatrenia, a tak bude vybraný ScaleN Triangle, ktorý má pravý uhol.

Príklady

-Ak sa považuje obdĺžnikový trojuholník, ktorého nohy majú dĺžky 3 a 4, potom podľa Pythagorovej vety možno dospieť k záveru, že hypotenus bude mať dĺžku 5. To znamená, že trojuholník je vyradený a má pravý uhol.

-Nech ABC je obdĺžnikový trojuholník s meraniami 1 a 2. Potom je dĺžka jej hypotenusu √5, ktorá dospela k záveru, že ABC je trojuholník obdĺžnika Scale.

Nie každý trojuholník mierky má pravý uhol. Môžete zvážiť trojuholník, ako je trojuholník nasledujúceho obrázku, ktorý je vyťažený, ale žiadny z jeho vnútorných uhlov nie je rovný.

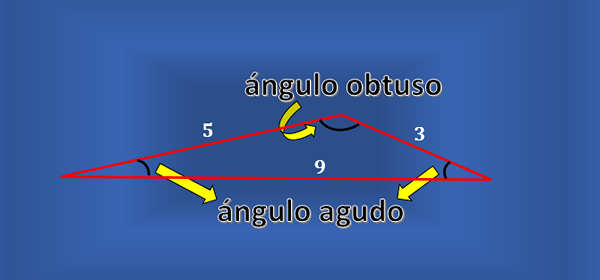Okrem toho nie každý pravý trojuholník je SCALENE. Ak uvažujete o pravicovom trojuholníku, ktorého nohy merajú obidva 1, potom hypotenus bude mať mieru √2. Preto je obdĺžnikový trojuholník izosceles.