Vektorový priestor základnej a rozmerov, axiómy, vlastnosti

A vektorový priestor Je to ne -epty set Vložka= alebo, vložka, W,…, ktorých prvky sú vektory. S nimi sa vykonávajú niektoré dôležité operácie, medzi ktorými vynikajú nasledujúce:

- Súčet medzi dvoma vektormi u + v ako výsledok z, ktorý patrí celku Vložka.

- Násobenie skutočného čísla α vektorom vložka: α vložka To dáva ďalší vektor a čo patrí Vložka.

Umelecká vízia vektorového priestoru. Zdroj: Pixabay

Na označenie vektora používame tučné písmo (vložka Je to vektor) a pre skaláry alebo čísla grécke písmená (α je číslo).

[TOC]

Axiómy a vlastnosti

Na to, aby ste boli vektorovým priestorom, musí sa splniť nasledujúcich osem axiómov:

1-conmutabilita: alebo +vložka = vložka +alebo

2-prenosnosť: (alebo + vložka) + W = alebo + ( vložka + W)

3-existencia nulového vektora 0 tak 0 + vložka = vložka

4-existencia opaku: opak vložka je (-vložka) , vzhľadom na to vložka + (-vložka) = 0

Distribúcia 5 produktov vzhľadom na vektorový súčet: α ( alebo + vložka ) = αalebo +αvložka

Distribúcia 6 produktov vzhľadom na skalárny súčet: (a + β)vložka = αvložka +pvložka

7-asociativita skalárneho produktu: a (p vložka) = (a β)vložka

8-číslo 1 Je to neutrálny prvok od: 1vložka = vložka

Príklady vektorových priestorov

Príklad 1

Vektory v rovine (R2) sú príkladom vektorového priestoru. Vektor v rovine je geometrický objekt, ktorý má veľkosť a smer. Je reprezentovaný orientovaným segmentom, ktorý patrí do uvedenej roviny a s veľkosťou úmerne k jeho veľkosti.

Súčet dvoch vektorov v rovine môže byť definovaný ako geometrická prevádzka druhého vektora po prvom. Výsledkom súčtu je orientovaný segment, ktorý začína od pôvodu prvého a dosiahne špičku druhého.

Na obrázku je možné poznamenať, že suma v R² je komutatívna.

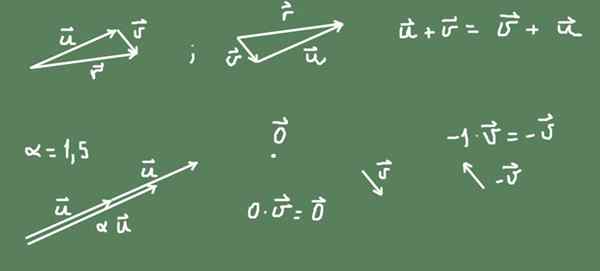Obrázok 2. Vektory vo vektorovom priestore lietadla. Zdroj: Self Made.

Produkt a číslo a je tiež definovaný vektorom. Ak je číslo kladné, zachová sa pôvodná vektorová adresa a veľkosť je α násobok pôvodného vektora. Ak je číslo záporné, adresa je opak a výsledná veľkosť vektora je absolútna hodnota čísla.

Vektor proti vektorovi akýkoľvek vložka je -vložka = (-1) vložka.

Nulový vektor je bod v rovine R2 a nulové číslo vektorom vedie k nulovému vektoru.

Všetky povedané je znázornené na obrázku 2.

Príklad 2

Súbor P Zo všetkých polynómov menších alebo rovnajúcich sa dvom, vrátane nulovej známky, tvoria set, ktorý spĺňa všetky axiómy vektorového priestoru.

Môže vám slúžiť: vzájomne sa vylučujú udalosti: Vlastnosti a príklady

Je polynóm p (x) = a x² + b x + c y q (x) = d x² + e x + f

Súčet dvoch polynómov je definovaný: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Súčet polynómov patriacich do celku P Je to komutatívne a tranzitívne.

Nulová polynóm patriaci k celku P Je to ten, ktorý má všetky svoje koeficienty rovnajúce sa nule:

0 (x) = 0 x² + 0 x + 0

Súčet a skalára je definovaný polynómom, ako je: a p (x) = a ∙ a x² + a ∙ b x + a ∙ c

Opačný polynóm p (x) je -p (x) = (-1) p (x).

Zo všetkých vyššie uvedených vyplýva, že sada P Zo všetkých polynómov menších alebo rovnajúcich sa dvom, je to vektorový priestor.

Príklad 3

Súbor M Zo všetkých matíc stĺpcov m nov x n, ktorých prvky sú skutočné vektorové priestory, vzhľadom na súčet matíc a produktu čísla maticou.

Príklad 4

Sada F kontinuálnych funkcií skutočnej premennej, tvorí vektorový priestor, pretože súčet dvoch funkcií je možné definovať, násobenie skalárnej funkcie, nulovou funkciou a symetrickou funkciou. Spĺňajú tiež axiómy, ktoré charakterizujú vektorový priestor.

Základňa a rozmer vektorového priestoru

Základňa

Sada lineárne nezávislých vektorov je definovaná ako základ vektorového priestoru tak, že z lineárnej kombinácie z nich je možné generovať akýkoľvek vektor tohto vektorového priestoru.

Lineárne kombinovanie dvoch alebo viacerých vektorov spočíva v znásobovaní vektorov pomocou niektorých skalárnych a potom ich vektorovo pridanie.

Napríklad vo vektorovom priestore vektora v troch rozmeroch tvorených Rilo sa používa kanonická báza definovaná jednotkovými vektormi (s veľkosťou 1) (s veľkosťou 1) Jo, J, klimatizovať.

Kde Jo = (1, 0, 0); J = (0, 1, 0); klimatizovať = (0, 0, 1). Sú to karteziánske alebo kanonické vektory.

Akýkoľvek vektor Vložka patriace k rčeniu je napísané ako Vložka = a Jo + b J + c klimatizovať, čo je lineárna kombinácia základných vektorov Jo, J, klimatizovať. Skaláry alebo čísla a, b, c sú známe ako karteziánske komponenty Vložka.

Hovorí sa tiež, že základné vektory vektorového priestoru tvoria sadu vektorového priestoru.

Rozmer

Rozmer vektorového priestoru je kardinálne číslo vektorovej základne pre uvedený priestor; To znamená, že počet vektorov, ktoré tvoria uvedenú základňu.

Tento kardinál je maximálny počet lineárne nezávislých vektorov tohto vektorového priestoru a zároveň minimálny počet vektorov, ktoré tvoria generujúcu sadu uvedeného priestoru.

Môže vám slúžiť: Štatistická populácia: Koncept, typy, príklady

Základy vektorového priestoru nie sú jedinečné, ale všetky základy toho istého vektorového priestoru majú rovnaký rozmer.

Vektorový podprostor

Vektorový podprostor vektorového priestoru V je podmnožina V, v ktorej sú rovnaké operácie definované ako vo V a spĺňa všetky axiómy vektorového priestoru. Preto bude subprostorom tiež vektorovým priestorom.

Príklad vektorového podprostora sú vektory, ktoré patria do roviny XY. Tento podprostor je podskupinou vektorového priestoru rozmernosti väčšiu ako sada vektorov patriacich do trojrozmerného priestoru XYZ.

Ďalším príkladom vektorového podskupiny S1 vektorového priestoru je všetky matice 2 × 2 so skutočnými prvkami, ktorý je definovaný nižšie:

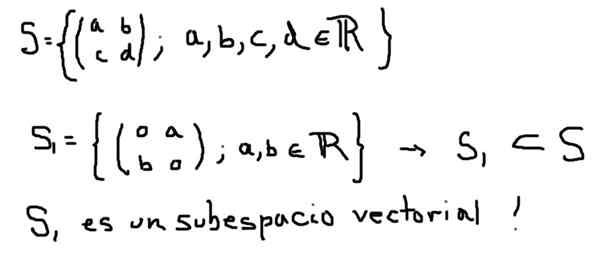
Na druhej strane, S2 definovaný nižšie, hoci je to podmnožina S, netvorí vektorový podprostor:

Vyriešené cvičenia

-Cvičenie 1

Byť vektormi V1= (1, 1, 0); V2= (0, 2, 1) a V3= (0, 0, 3) v R³.

a) Dokážte, že sú lineárne nezávislé.

b) Dokážte, že tvoria základňu v R³, pretože akýkoľvek zoznam (x, y, z) je možné písať ako lineárna kombinácia V1, V2, V3.

c) Nájdite komponenty zoznamu Vložka = (-3,5,4) na základni V1, V2, V3.

Riešenie

Kritériom na demonštráciu lineárnej nezávislosti je stanoviť nasledujúcu sadu rovníc v a, β a y

a (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

V prípade, že jediným riešením tohto systému je a = β = γ = 0, potom sú vektory lineárne nezávislé, inak nie sú.

Na dosiahnutie hodnôt a, β a y navrhujeme nasledujúci systém rovníc:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Prvý vedie k a = 0, druhému a = -2 ∙ β, ale ako a = 0 potom β = 0. Tretia rovnica znamená, že γ = (-1/3) β, ale ako β = 0 potom γ = 0.

Odpovedať

Dospelo sa k záveru, že ide o sadu lineárne nezávislých vektorov v R³ .

Odpoveď B

Teraz napíšte zoznam (x, y, z) ako lineárnu kombináciu V1, V2, V3.

(x, y, z) = a v1 + β v2 + y v3 = a (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Môže vám slúžiť: Tukey Test: Čo je v prípade príkladu vyriešené cvičenie

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Kde máš:

α = x

a + 2 β = y

β + 3 γ = z

Prvý označuje a = x, druhý β = (y-x)/2 a tretí γ = (z- y/2 +x/2)/3. Týmto spôsobom sme našli generátory a, β a y akéhokoľvek zoznamu rilo 

Odpoveď c

Nájdeme komponenty zoznamu Vložka = (-3,5,4) na základni V1, V2, V3.

Zodpovedajúce hodnoty nahrádzame vo vyššie uvedených výrazoch pre generátory.

V tomto prípade máme: α = -3; p = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

To je:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Konečne:

Vložka = -3 V1 + 4 V2 + 0 V3

Uvádzame to k záveru V1, v2, v3 Tvoria základňu vo vektorovom priestore r³ dimenzie 3.

-Cvičenie 2

Exprimujte polynóm P (t) = t² + 4T -3 ako lineárna kombinácia p1 (t) = t² -2t + 5, p2 (t) = 2t² -3t a p3 (t) = t + 3.

Riešenie

P (t) = x p1 (t) + a p2 (t) + z p3 (t)

kde čísla x, y, z musia byť určené.

Vynásobením a zoskupením výrazov s rovnakým stupňom v t: Získa sa:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Čo nás vedie k nasledujúcemu systému rovníc:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Riešenia tohto systému rovníc sú:

x = -3, y = 2, z = 4.

To je:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Cvičenie 3

Ukážte, že vektory V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) a V3= (2, 1, -1, 1) r⁴ sú lineárne nezávislé.

Riešenie

Lineárne kombinujeme tri vektory V1, V2, V3 A požadujeme, aby táto kombinácia pridala nulovú prvok r⁴

do V1 + b V2 + c V3 = 0

To znamená,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

To nás vedie k nasledujúcemu systému rovníc:

A + B + 2 C = 0

B + C = 0

-A - C = 0

2 A + B + C = 0

Odčítanie prvej a štvrtej, ktorú máme: -a + c = 0, čo znamená a = c.

Ale ak sa pozrieme na tretiu rovnicu, musíme = -c. Jediný spôsob, ako splniť a = c = (-c) je, že C je 0, a preto bude tiež 0.

A = c = 0

Ak nahradíme tento výsledok v prvej rovnici, dospel sme k záveru, že b = 0.

Nakoniec a = b = c = 0, takže sa dá dospieť k záveru, že vektory V1, V2 a V3 sú lineárne nezávislé.

Odkazy

1. Lipschutz, s. 1993. Lineárna algebra. Druhé vydanie. McGraw - Hill. 167 - 198.