Štandardná chyba odhadu, ako sa vypočítava, príklady, cvičenia

On Chyba štandardného odhadu Zmerajte odchýlku vo vzorkovej hodnote populácie. To znamená, že chybová chyba štandardného odhadu meria možné variácie priemeru vzorky vzhľadom na skutočnú hodnotu priemeru populácie.

Napríklad, ak chcete poznať priemerný vek populácie krajiny (priemer obyvateľov), je prijatá malá skupina obyvateľov, ktorú nazývame „predstaveniami“. Z toho sa extrahuje priemerný vek (priemer vzorky) a predpokladá sa, že populácia má tento priemerný vek so štandardnou chybou odhadu, ktorá sa mení viac -menej.

M. W. Toews [CC po 2.5 (https: // creativeCommons.Org/licencie/BY/2.5)]

Je potrebné poznamenať, že je dôležité nezamieňať štandardnú odchýlku so štandardnou chybou a štandardnou chybou odhadu:

1- Štandardná odchýlka je miera disperzie údajov; to znamená, že ide o mieru variability populácie.

2- Štandardná chyba je miera variability vzorky, vypočítaná na základe štandardnej odchýlky populácie.

3- Štandardná chyba odhadu je miera chyby, ktorá sa urobí pri odobratí priemeru vzorky ako odhad priemeru populácie.

[TOC]

Ako sa vypočítava?

Štandardná chyba odhadu sa môže vypočítať pre všetky opatrenia získané vo vzorkách (napríklad štandardná priemerná chyba odhadu alebo štandardná chyba štandardného odhadu odchýlky) a meria chybu, ktorá sa urobí pri odhadovaní skutočnej populačnej miery z hodnoty vzorky

Zo štandardnej chyby odhadu je vytvorený interval spoľahlivosti zodpovedajúceho opatrenia.

Môže vám slúžiť: Reverzná matica: Výpočet a cvičenie vyriešené

Všeobecná štruktúra vzorca pre štandardnú chybu odhadu je nasledovná:

Chyba štandardného odhadu = ± koeficient dôveryhodnosti * Štandardná chyba

Koeficient dôvery = limitná hodnota štatistiky vzorky alebo distribúcie vzorkovania (normálny alebo Gauss Bell, Student T, okrem iného) pre určitý interval pravdepodobností.

Štandardná chyba = štandardná odchýlka populácie vydelená druhou odmocninou veľkosti vzorky.

Koeficient spoľahlivosti naznačuje množstvo štandardných chýb, ktoré sú ochotné pridať a odpočítať, aby mali určitú úroveň dôvery vo výsledky.

Príklady výpočtu

Predpokladajme, že sa snažíte odhadnúť podiel ľudí v populácii, ktorí majú správanie, a chcete mať 95% dôveru vo svojich výsledkoch.

Vzorka N ľudí sa odoberie a určuje sa podiel vzorky P a jej doplnok Q.

Chyba štandardného odhadu (EEE) = ± koeficient dôveryhodnosti * Štandardná chyba

Koeficient dôvery = z = 1.96.

Štandardná chyba = druhá odmocnina dôvodu medzi produktom podielu vzorky pre jej doplnok a veľkosťou vzorky n.

Zo štandardnej chyby odhadu sa stanoví interval, v ktorom sa stanoví interval, v ktorom sa podieľa podiel populácie alebo podiel vzoriek iných vzoriek, ktoré sa môžu vytvoriť z tejto populácie, s 95% úrovňou spoľahlivosti:

P -eee ≤ podiel populácie ≤ P + EEE

Vyriešené cvičenia

Cvičenie 1

1- Predpokladajme, že sa snažíte odhadnúť podiel ľudí v populácii, ktorí majú prednosť obohatenému dojničnému vzorcu, a chcete mať 95% dôveru vo svojich výsledkoch.

Môže vám slúžiť: Syntetické rozdelenie

Vzorka 800 ľudí sa odoberie a je určené, že 560 ľudí vo vzorke má preferencie obohateného vzorca mliečnych výrobkov. Stanovte interval, v ktorom možno očakávať podiel populácie a podiel ďalších vzoriek, ktoré je možné odobrať z populácie, s 95% dôverou

a) Vypočítajme pomer vzorky P a jej doplnok:

P = 560/800 = 0.70

Q = 1 -p = 1 -0.70 = 0.30

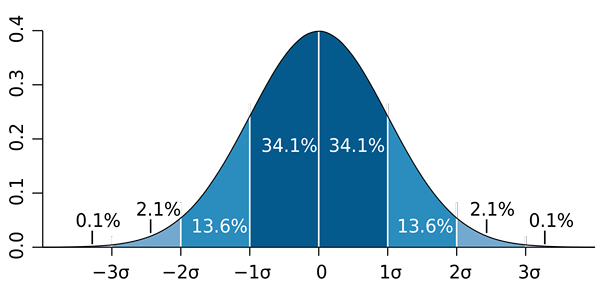
b) Je známe, že podiel sa blíži k normálnemu rozdeleniu k vzorkám veľkej veľkosti (viac ako 30). Potom sa použije So -Called pravidlo 68 - 95 - 99.7 a musíte:

Koeficient dôvery = z = 1.96

Štandardná chyba = √ (p*q/n)

Chyba štandardného odhadu (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Zo štandardnej chyby odhadu sa stanoví interval, v ktorom sa očakáva podiel populácie s 95% úrovňou spoľahlivosti:

0.70 -0.0318 ≤ podiel populácie ≤ 0.70 + 0.0318

0.6682 ≤ podiel populácie ≤ 0.7318

Môžete očakávať, že 70% vzorový pomer zmeny až 3.18 percentuálnych bodov, ak má inú vzorku 800 jednotlivcov alebo že skutočný podiel populácie je medzi 70 - 3.18 = 66.82% a 70 + 3.18 = 73.18%.

Cvičenie 2

2- Vezmeme si od Spiegel a Stephens, 2008, nasledujúca prípadová štúdia:

Z celkových známok matematiky prvých študentov univerzity sa odobrala náhodná vzorka 50 kvalifikácií, v ktorej bol priemer zistený 75 bodov a štandardná odchýlka, 10 bodov, 10 bodov. Aké sú 95% limity spoľahlivosti pre odhad priemeru matematickej kvalifikácie univerzity?

Môže vám slúžiť: Aký je vzťah medzi oblasťami Rhombus a obdĺžnik?

a) Vypočítajme štandardnú chybu odhadu:

95%koeficient spoľahlivosti = z = 1.96

Štandardná chyba = s/√n

Chyba štandardného odhadu (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Zo štandardnej chyby odhadu je stanovený interval, v ktorom je stanovený priemer populácie alebo priemer inej vzorky 50, s úrovňou spoľahlivosti 95%:

50 -2.7718 ≤ priemer populácie ≤ 50 + 2.7718

47.2282 ≤ Populácia priemer ≤ 52.7718

c) Môžete očakávať, že priemer vzorky sa zmení až na 2.7718 bodov Ak sa odoberie iná vzorka 50 stupňov alebo že skutočný priemer matematických stupňov populácie univerzity je medzi 47.2282 bodov a 52.7718 bodov.

Odkazy

1. Abraira, V. (2002). Štandardná odchýlka a štandardná chyba. Časopis. Na webe obnovený.Archív.orgán.
2. Rumsey, D. (2007). Stredná štatistika pre figuríny. Wiley Publishing, Inc.
3. Salinas, h. (2010). Štatistika. Zotavené z rohože.Uda.Cl.
4. Sokal, r.; Rohlf, f. (2000). Biometria. Zásady a prax štatistík v biologickom výskume. Tretie vydanie. Edície Blume.
5. Spiegel, m.; Stephens, L. (2008). Štatistika. Štvrté vydanie. McGraw-Hill/Inter-American z Mexika S. Do.
6. Wikipedia. (2019). 68-95-99.7 Pravidlo. Získaný z.Wikipedia.orgán.
7. Wikipedia. (2019). Štandardná chyba. Získaný z.Wikipedia.orgán.