Vzorce a rovnice rotačnej rovnováhy, príklady, cvičenia

Tvrdí sa, že rozšírené telo je v rotačná rovnováha Keď súčet krútiacich momentov, ktoré na ňu konajú, je nula. To neznamená, že objekt je nevyhnutne v pokoji, ale skôr, že neexistuje žiadny čistý trend na zmenu stavu pohybu na inú.

Objekt, ktorý sa pohybuje konštantnou rýchlosťou, tak robí po priamke a my ho môžeme zvážiť v rotačnej rovnováhe. Teraz sa objekty točia, pretože existujú sily, ktoré na nich konajú takým spôsobom, že ide o rotáciu. Schopnosť sily vytvárať rotáciu, nazývanú krútiaci moment alebo Torca, Závisí to nielen od intenzity sily, ale aj tam, kde sa používa.

postava 1. Vzúčací most na obrázku bol navrhnutý tak, aby bol v rovnováhe rotácie. Zdroj: Wikimedia Commons.

Uznávame to okamžite, keď sa otvoria zatvorené dvere: sila sa nikdy nanáša v blízkosti pántov, ale ďaleko od nich, takže rukoväť je umiestnená čo najďalej, vedľa dverí dverí.

Pánty prechádzajú osou rotácie dverí. Trvá na tom, aby ste ho tlačili veľmi blízko k závesom, musíte urobiť veľké úsilie, aby sa dvere trochu pohybovali.

V literatúre je krútiaci moment s rôznymi názvami: moment torzie, torzie, moment sily a torca. Všetky sú synonymá.

Potrebujeme teda poznať krútiace momenty, ktoré pôsobia na objekt, aby stanovili podmienku rovnováhy rotácie.

[TOC]

Stav rotačnej rovnováhy

Podmienka rotačnej rovnováhy je:

Súčet všetkých momentov alebo krútiacich momentov, ktoré pôsobia na tele, vypočítané s ohľadom na akúkoľvek os, musí byť neplatný.

Dotknutý objekt sa musí rozšíriť, pretože častice, podľa definície, majú iba prekladovú rovnováhu.

Môžete vám slúžiť: Newtonov druhý zákon: Aplikácie, experimenty a cvičenia

Na tele môžu byť aplikované sily a stále existuje rotačná rovnováha, zatiaľ čo sily ju neotáčajú.

Môže dôjsť aj k pohybu, dokonca zrýchlený, ale vždy pozdĺž priamky, pretože nie všetky sily spôsobujú vzhľad krútiacich momentov. Tieto sa objavujú, keď sily nekonajú celú tú istú líniu konania.

Krútiaci moment alebo moment sily

Krútiaci moment je označený gréckymi textami τ, v odvážne písmo Pretože je to vektor a odlišujeme ho od jeho veľkosti alebo modulu, čo je skalár. Závisí to od aplikovanej sily F, vektora r ktorý je nasmerovaný z osi rotácie alebo do bodu použitia sily a nakoniec z uhla medzi týmito dvoma vektormi.

Správny vzťah medzi týmito veľkosťami je stanovený prostredníctvom vektorového produktu:

τ = r X F

A modul krútiaceho momentu, označený bez tučného tuku, je:

τ = r⋅f⋅sen θ

Kde 9 je uhol medzi r a F. Momentové jednotky sú jednoducho N⋅m v medzinárodnom systéme.

Na obrázku je anglický kľúč, s ktorým je určený. Z tohto dôvodu sú skúšané dve sily F_Do a F_B.

F_Do je bližšie k O a má vektor r_Do alebo kratšie rameno páky, preto nevyrába toľko krútiaceho momentu a sily F_B, To má rovnakú veľkosť, ale má vektor r_B väčší.

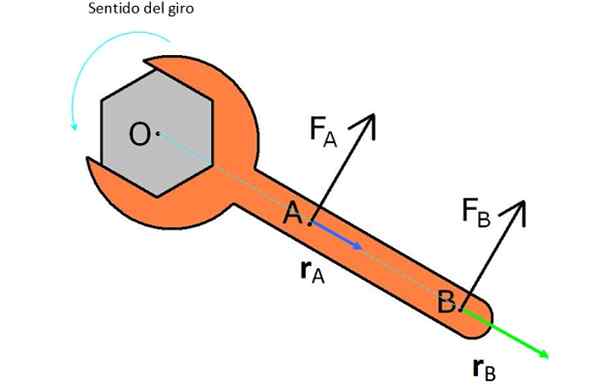Obrázok 2. Sily a zbrane aplikované na anglický kľúč, aby sa obrátil v rozpore s ihlami pre hodiny. Zdroj: Wikimedia Commons.

Všimnite si, že ak chcete otočiť maticu v pláne, musíte aplikovať sily v opačnom smere, ako sa objavia na obrázku.

Smer a zmysel pre krútiaci moment

Keďže krútiaci moment je výsledkom krížového produktu medzi vektormi pevnosti a polohy, ktoré sú v rovine anglického kľúča, krútiaci moment musí byť vektorom kolmým na túto rovinu, tj smerom k čítačke alebo vo vnútri stránky.

Môže vám slúžiť: atmosférický tlak: normálna hodnota, ako sa merala, príklady

Konvenciou je krútiaci moment pozitívny, ak sa vytvára v opačnom smere od hodinových ihiel, a negatívny, ak tak urobí v smere k hodinám.

Smer a smer výsledného krútiaceho momentu sú ľahko určené pravidlom pravej ruky uvedenej nižšie:

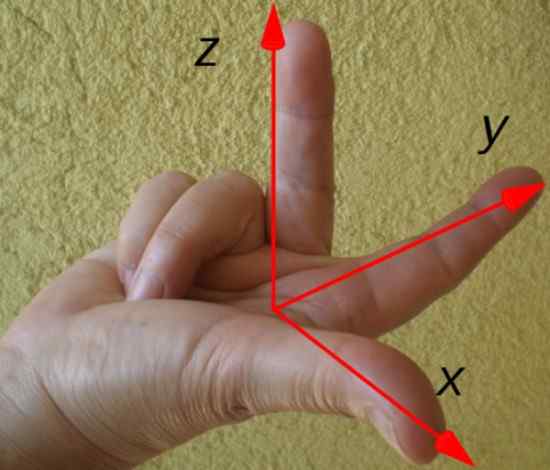Obrázok 3. Pravá ruka na určenie smeru a smeru troce. Zdroj: Wikimedia Commons.

Ukazovák body podľa polohového vektora r, Prostredný prst podľa sily F A palec signalizuje smer a smer krútiaceho momentu τ. V tomto príklade je krútiaci moment nasmerovaný pozdĺž osi x podľa výkresu súradnicových osí.

Vzorce a rovnice

Ak momenty konajú na tele τ₁, τ_2, τ_3… τ_Jo, Sieť alebo výsledný krútiaci moment τ_n Je to vektorový súčet všetkých:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Jo

Pri zhrnutí sčítania zostáva:

τ_n = ∑ τ_Jo

Rovnovážna podmienka je vyjadrená matematicky takto:

τ_n = 0

O dobre:

∑ τ_Jo = 0

Kde moment τ, Pokiaľ ide o určitú os O, počíta sa podľa:

τ = r X F

A ktorého veľkosť je:

τ = r⋅f⋅sen θ

Príklady

-U ľudí a zvierat je hmotnosť sila, ktorá môže spôsobiť krútiaci moment a otáčanie a pád.

Ľudia si zvyčajne udržiavajú takú pozíciu, že pri chôdzi ich udržiava v rovnováhe rotácie, pokiaľ sa nevykonáva športová činnosť, ako napríklad gymnastika, korčuľovanie alebo šport všeobecne.

-Dve deti, ktorým sa podarilo zostať horizontálny v rocker ani hore a dole Sú v rotácii rovnováhy.

-Keď sú taniere rovnováhy vyvážené, systém je v rotačnej rovnováhe.

-Oznámenia a semafory, ktoré visia na uliciach a uliciach, sú tiež v rotačnej rovnováhe. Ak sú káble, ktoré ich držajú, zlomené, stratí sa táto rovnováha a oznámenie je visí alebo padá.

Môže vám slúžiť: Priemerné zrýchlenie: Ako sa vypočítava a vyrieši

-Závesné mosty ako Golden Gate v San Franciscu a most na obrázku 1.

Cvičenie

Lišta podporovaná podperou zobrazenou na obrázku je veľmi ľahký. Sila, ktorú uplatňuje podpora, je F a na konci sily uplatňuje Do.

Žiada sa o výpočet veľkostí týchto síl s ohľadom na to, že systém je v rovnováhe prekladu a rotácie.

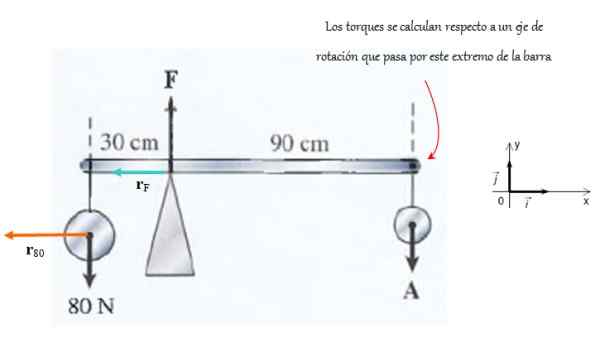Obrázok 4. Na tomto barovom silách konajú takým spôsobom, že zostáva v rotačnej rovnováhe. Zdroj: f. Zapata.

Riešenie

Keďže sa systém nepohybuje, súčet síl je zrušený. Všetky sú vertikálne a môžete pracovať s veľkosťou. Pozitívny zmysel je teda hore a negatívny dole, preto:

F - 80 - a = 0

Teraz sa používa rotačná rovnovážna podmienka, pre ktorú musíte zvoliť ľubovoľnú os rotácie. V tomto prípade je vybraný na konci vpravo, takže vektor r_Do Buďte null, týmto spôsobom moment, ktorý vykonáva Do, ale iba tí z F a sila vľavo.

Krútiaci moment vyrobený F Je to podľa pravidla pravej ruky a súradnicový systém zobrazený:

τ_F = r_F X F = 0.9 f (-klimatizovať) N.m

Je nasmerovaný na obrazovku a má negatívne znamenie. Zatiaľ čo krútiaci moment produkovaný silou 80 N je:

τ = 80 x 1.dvadsať (klimatizovať) N⋅m = 96 (klimatizovať) N⋅m

Tento krútiaci moment je nasmerovaný z obrazovky a je priradený kladný znak. Pretože existuje rotačná rovnováha:

96 - 0.9⋅f = 0

Veľkosť F je:

F = (96/0.9) n = 106.7 n

A keďže systém je v prekladovej rovnováhe, súčet síl je zrušený. To nám umožňuje vyčistiť veľkosť Do:

F - a - 80 n = 0

Preto:

A = 106.7 - 80 n = 26.7 n.

Odkazy

1. Rex, a. 2011. Základy fyziky. Pearson.
2. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa.
3. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. Pearson.
4. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil.
5. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. McGraw Hill.