Potenciálne energetické charakteristiky, typy, výpočet a príklady

Ten potenciálna energia Je to energia, ktorú majú telá v rámci svojej konfigurácie. Keď objekty interagujú, existujú sily schopné robiť prácu a táto schopnosť pracovať, ktorá je uložená v dispozícií, ktorú majú, môže preložiť do energie.

Napríklad ľudské bytosti využili potenciálnu energiu vody, ktorá klesá od nepamäti, najprv rotujúce mlyny a potom do vodných rastlín.

Niagara Falls: Obrovský gravitačný potenciál energetickej rezervy. Zdroj: Pixabay.

Na druhej strane, veľa materiálov má pozoruhodnú schopnosť pracovať deformovaním a potom sa vrátiť do pôvodnej veľkosti. A za iných okolností usporiadanie elektrického náboja umožňuje ukladanie energie elektrického potenciálu, napríklad v kondenzátore.

Potenciálna energia ponúka veľa možností na transformáciu na iné užitočné formy energie, a preto je dôležitosť poznania zákonov, ktoré ich riadia. 

[TOC]

Pôvod potenciálnej energie

Potenciálna energia objektu má svoj pôvod v silách, ktoré ho ovplyvňujú. Potenciálna energia je však skalárnou veľkosťou, zatiaľ čo sily sú vektor. Preto na špecifikáciu potenciálnej energie stačí na označenie jej číselnej hodnoty a vybratých jednotiek.

Ďalšou dôležitou kvalitou je typ sily, s ktorou je možné uložiť potenciálnu energiu, pretože žiadna sila nemá túto cnosť. Iba konzervatívne sily ukladajú potenciálnu energiu v systémoch, na ktorých konajú.

Konzervatívna sila je taká, pre ktorú práca nezávisí od trajektórie, po ktorej nasleduje objekt, ale iba od východiskového bodu a bodu príchodu. Sila, ktorá poháňa vodu, je gravitácia, čo je konzervatívna sila.

Na druhej strane, elastické a elektrostatické sily majú túto kvalitu, preto s nimi je spojená potenciálna energia.

Sily, ktoré nespĺňajú vyššie uvedené požiadavky, sa nazývajú nekonzervatívni; Príklad z nich je v trení a odolnosti proti vzduchu.

Typy potenciálnej energie

Pretože potenciálna energia vždy pochádza z konzervatívnych síl, ako sú už uvedené sily, hovorí sa o gravitačnej potenciálnej energii, elastickej potenciálnej energii, elektrostatickej potenciálnej energii, energetickej energii jadrového potenciálu a potenciálnej energii Energy Energy.

Gravitačný potenciál

Každý objekt má potenciálnu energiu založenú na výške, ktorú majú vzhľadom na zem. Tento jednoduchý vzhľad, ktorý sa objaví, ilustruje, pretože vodopád je schopný zvýšiť turbíny a nakoniec sa transformuje na elektrinu. Príklad tu uvedených lyžiarov tiež ukazuje vzťah hmotnosti a výšky s energiou gravitačného potenciálu.

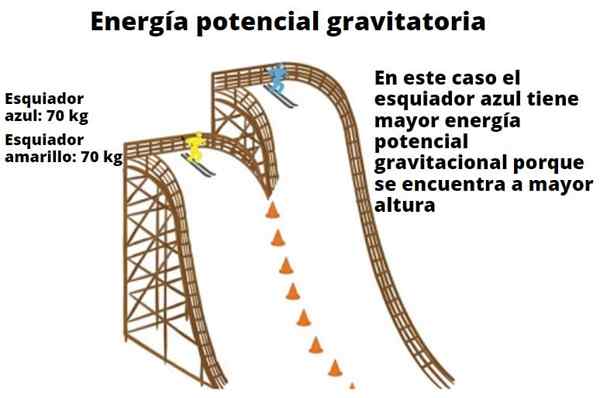
Ďalším príkladom je horský automobil, ktorý má väčšiu potenciálnu energiu, keď je v určitej výške na zemi. Akonáhle dosiahne úroveň podlahy, jej výška sa rovná nule a všetka jej potenciálna energia sa transformovala na kinetickú energiu (pohybová energia).

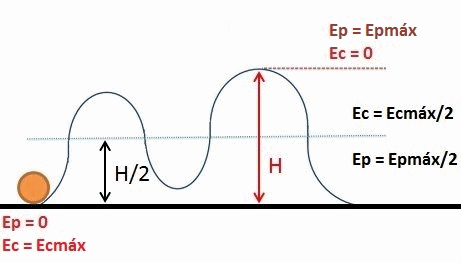Animácia ukazuje výmenu medzi gravitačným potenciálom energie a kinetickou energiou, objektu, ktorý sa pohybuje po horskej dráhe. Súčet oboch energií, nazývaný mechanická energia, je počas celého pohybu konštantný. Zdroj: Wikimedia Commons.

Elastická potenciálna energia

Objekty, ako sú pružiny, oblúky, kuše a ligy, sú schopné uchovávať elastickú potenciálnu energiu.

Keď je oblúk napätý, brankár vykonáva prácu, ktorá je uložená ako potenciálna energia systému ARC-FET. Keď sa oblúk uvoľní, táto energia sa transformuje na pohyb šípky. Zdroj: Pixabay.

Elasticitu tela alebo materiálu je opísaný Hookeovým zákonom (až do určitých limitov), ​​ktorý nám hovorí, že sila schopná vyvíjať pri stlačení alebo natiahnutí je úmerná jeho deformácii.

Môže vám slúžiť: feromagnetizmus: materiály, aplikácie a príklady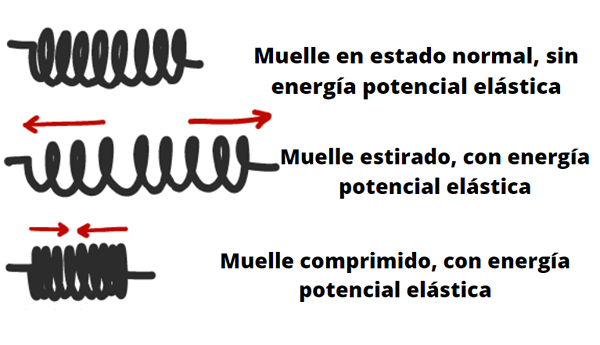

Napríklad v prípade pružiny alebo pružiny to znamená, že čím viac sa zmenšuje alebo sa roztiahne, tým väčšia je sila, ktorá sa dá vyvíjať na objekt umiestnený na jednom konci.

Elektrostatická energia

Je to energia, ktorú majú elektrické poplatky v rámci svojej konfigurácie. Elektrické náboje toho istého znaku sú odrazené, takže na umiestnenie niekoľkých pozitívnych zaťažení - alebo negatívnych - v určitej pozícii musí externý agent pracovať. Inak by mali tendenciu oddeliť sa.

Táto práca je uložená spôsobom, akým sa nachádzali zaťaženia. Čím bližšie je zaťaženie toho istého znaku, tým väčšia je potenciálna energia, ktorá bude mať konfigurácia. Stáva sa to naopak, pokiaľ ide o rôzne zaťaženia znakov; Keď priťahujú, čím bližšie sú, tým menej potenciálnej energie majú.

Jadrový potenciál

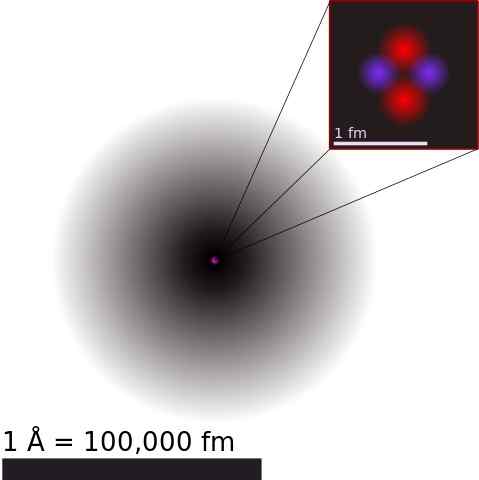Približný atóm hélia. V jadre sú protóny reprezentované červenou farbou a neutróny v modrej farbe.

Atómové jadro je zložené protóny a neutróny, ktoré sa všeobecne nazývajú Jadro. Prvý z nich má pozitívny elektrický náboj a druhý je neutrálny.

Pretože sú aglomerované v malom priestore za fantáziou a vedia, že zaťaženie toho istého znamenia sa odrazuje, stojí za to sa opýtať, ako zostáva atómové jadro súdržné.

Odpoveď je v iných silách okrem elektrostatického odporu, typické pre jadro, ako je silná jadrová interakcia a slabá jadrová interakcia. Sú to veľmi intenzívne sily, ktoré ďaleko presahujú elektrostatickú silu.

Chemický potenciál

Táto forma potenciálnej energie vychádza z toho, ako sú k dispozícii atómy a molekuly látok, podľa rôznych typov chemických väzieb.

Ak je uvedená chemická reakcia, táto energia sa môže transformovať na iné typy, napríklad elektrickou batériou alebo batériou.

Príklady potenciálnej energie

Potenciálna energia je prítomná v každodennom živote v mnohých aspektoch. Pozorovanie jeho účinkov je také ľahké ako umiestnenie akéhokoľvek objektu v určitej výške a mať istotu, že sa môže kedykoľvek hodiť alebo spadnúť.

Tu je niekoľko prejavov, ktoré boli opísané v súčasnosti, už opísané:

-Húsenkové dráhy

-Autá alebo gule sa valia z kopca

-Luky a šípy

-Elektrické batérie

-Kyvadlo

Keď je jedna z extrémnych guľôčok uvedená do pohybu, pohyb sa prenáša do ostatných. Zdroj: Pixabay.

-Hojdať sa v hojdačke

-Rozľahlosť

-Použite stiahnuteľné pero.

Pozri: Príklady potenciálnej energie.

Výpočet energie

Potenciálna energia závisí od práce, ktorá vytvára silu, a to zase nezávisí od trajektórie, potom je možné potvrdiť, že:

-Ak sú A a B dva body, práca W_AB  Potrebné ísť z A do B, rovná sa potrebnej práci, ktorú treba ísť z B do a. Preto: W_AB = W_BA, tak:

W_AB + W_BA = 0

-A ak sú testované dve rôzne trajektórie 1 a 2, aby sa pripojili k týmto bodom A a B, práca vykonaná v oboch prípadoch je tiež rovnaká:

 W₁ = W₂.

V každom prípade objekt zažije zmenu potenciálnej energie:

Zmena = konečná potenciálna energia - počiatočná potenciálna energia

ΔU = u_Konečný - Alebo_{počiatočný} = U_B - Alebo_Do

Potenciálna energia objektu je definovaná ako negatív práce vykonanej silou (konzervatívna):

ΔU = -W_AB

Ale ako prácu je definovaná týmto integrálom:

Môže vám slúžiť: 31 typov sily vo fyzike a ich charakteristiky

Kde F a dr (s tučným písmom alebo šípkou) sú vektory pevnosti a posunu. S ohľadom na to je zmena potenciálnej energie negatívom tohto integrálu:

Pre konzervatívne sily, ako je opísané, sa integrál ľahko vypočíta. 

Všimnite si, že jednotky potenciálnej energie sú rovnaké ako jednotky práce. V medzinárodnom systéme, ak je jednotka joule, ktorá je skrátená a rovnocenná s 1 Newton X Metro, anglický fyzik James Joule (1818-1889).

Medzi ďalšie jednotky pre energiu patrí Ergio v systéme CGS, librová noha, btU (Britská tepelná jednotka), kalórie a kilowatt-horara.

Pozrime sa na niektoré konkrétne prípady, ako vypočítať potenciálnu energiu.

Výpočet gravitačnej potenciálnej energie

V blízkosti zemského povrchu je sila gravitačných bodov vertikálne nadol a jeho veľkosť je daná rovnicou Hmotnosť x gravitácia.

Označovanie vertikálnej osi písmenom „y“ a priradením tejto adrese vektor jednotky J, pozitívne a negatívne, zmena potenciálnej energie, keď sa telo pohybuje z y = y_Do až do y = y_B je:

Kde m predstavuje telo tela a g Hodnota zrýchlenia gravitácie. Ak ste vybraní a_Do = 0 ako referenčná úroveň na zemi, v ktorej je u fixovaný ako 0, máte:

U (y) = mgy

Výpočet elastickej potenciálnej energie

Hookeov zákon nám hovorí, že sila je úmerná deformácii:

F = -K.X

Tu X Je to deformácia a klimatizovať Je to konštanta pružiny, ktorá naznačuje, aké tuhé je. Prostredníctvom tohto výrazu sa vypočíta elastická potenciálna energia, berúc do úvahy Jo Je to jednotkový vektor v horizontálnom smere:

Pri výbere Alebo_Do = 0 v  X_Do, Predchádzajúci výraz je funkcia U (x) Pre potenciálnu energiu jari:

U (x) = ½ kx²

Výpočet energie elektrostatického potenciálu

Ak máte presný elektrický náboj, vyrába elektrické pole, ktoré vníma ďalšie presné zaťaženie Otázka, A čo na ňom funguje pri prechode z jednej polohy na druhú uprostred poľa. Elektrostatická sila medzi dvoma špecifickými zaťaženiami má radiálny smer, symbolizovaný cez jednotkový vektor r:

 Tu klimatizovať_a Je to elektrostatická alebo konštantná konštanta Coulomb, ktorej hodnota je klimatizovať_a ≈ 9 x 10⁹  N.m² /C² V jednotkách medzinárodného systému. Z toho vyplýva:

 Výber u = 0, keď r_Do → ∞, zostáva:

Vyriešené cvičenia

- Cvičenie 1: pružina, ktorá sa tiahne

Pružina, ktorej konštanta je klimatizovať = 10.0 n/cm spočiatku sa tiahne 1.00 cm od jeho rovnovážnej dĺžky. Žiada sa o výpočet dodatočnej energie potrebnej na roztiahnutie pramenia až do 5.00 cm za svoju rovnovážnu dĺžku.

Riešenie 

Priamo nahradenie x = 1.00 cm v rovnici pre u (x).CM, ale centimetre sa musia stať metermi, aby získali energiu v jouloch:

U (1) = 0.5 x 10.0 n/cm x (1.00 cm)² = 5 n. cm = 0.05 J; U (5) = 0.5 x 10.0 n/cm x (5.00 cm)² = 125 n.cm = 1.25 J

Preto je rozdiel v požadovanej energii 1.25 - 0.05 J = 1.20 j.

- Cvičenie 2: Konzervatívne a nekonzervačné sily

Z odpočinku sa uvoľňuje malý blok od bodu. Odtiaľ vstupuje na dlhý drsný horizontálny povrch s dynamickým koeficientom trenia μ_{klimatizovať} = 0.2. Nájdite v akej vzdialenosti od bodu B zastaví, za predpokladu, že h_Do= 3 m.

Môže vám slúžiť: Barrada Spiral Galaxy: Formation, Evolution, Charakteristika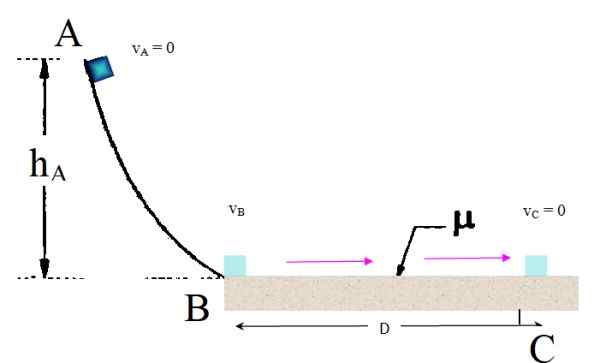Obrázok napríklad 1. Zdroj: f. Zapata.

Riešenie 

Keď je blok vo výške h_Do Pokiaľ ide o podlahu, má gravitačnú potenciálnu energiu kvôli svojej výške. Po prepustení sa táto potenciálna energia postupne stáva kinetickou energiou a keď prechádza hladkou zakrivenou ramou, jej rýchlosť sa zvyšuje.

Počas cesty z A do B sa rovnice rovnomerne rozmanitého priamočiara. Zatiaľ čo gravitácia je zodpovedná za pohyb bloku, pohyb, ktorý tento prežíva.

Ochrana energie na trase AB

Keďže však gravitácia je konzervatívna sila av rampe, nie je možné trenie, zachovanie mechanickej energie sa môže použiť na nájdenie rýchlosti, keď dosiahne koniec rampy:

Mechanická energia pri A = mechanická energia v B

m.g.h_Do + ½ m.vložka_Do² = m.g.h_B + ½ m.vložka_B²

Výraz sa zjednodušuje tým, že sa všimne, že hmota sa objaví v každom termíne. Sa uvoľňuje z REST V_Do = 0. A h_B Je na úrovni zeme, h_B = 0. S týmito zjednodušeniami sa výraz redukuje na:

vložka_B² = Gh_Do

Práca vykonaná trením v sekcii BC

Teraz blok začína svoju cestu v drsnej časti touto rýchlosťou a nakoniec sa zastaví v bode C. Preto V_C = 0. Mechanická energia sa už nezachová, pretože trenie je disipatívna sila, ktorá vykonala prácu v bloku danom:

W_{dotýkať sa} = -Frue trenia x vzdialenosť prešla

Táto práca má negatívne znamenie, pretože kinetické trenie sa spomaľuje na objekt a je proti jeho pohybu. Veľkosť kinetického trenia F_{klimatizovať}  je:

F_{klimatizovať} = μ_{klimatizovať} .N

Kde n je veľkosť normálnej sily. Normálna sila je vyvíjaná povrchom na bloku a keďže povrch je úplne vodorovná, pretože vyvažuje hmotnosť P = mg, Preto veľkosť normálu je:

N = mg

Čo vedie k:

F_{klimatizovať} = μ_{klimatizovať} .mg

Práca, ktorá F_{klimatizovať} Robí na bloku: W_{klimatizovať} = - f_{klimatizovať} .D =- μ_{klimatizovať} .mg.D.

Výpočet zmien mechanickej energie

Táto práca je rovnocenná so zmenou mechanickej energie, ktorá sa počíta takto:

Mechanická energia v C - mechanická energia pri B =

ΔE_m = (U_C +Klimatizovať_C)- (alebo_B + Klimatizovať_B) = μ_{klimatizovať} .mg.D

V tejto rovnici sú niektoré pojmy, ktoré sú zrušené: K_C = 0, pretože blok sa zastaví v C a je tiež zrušený u_C = U_B, za to, že sú tieto body na úrovni zeme. Zjednodušenie vedie k:

- Klimatizovať_B = - μ_{klimatizovať} .m.g.D

½ m.vložka_B² = μ_{klimatizovať} .m.g.D

Cesto je opäť zrušené a dá sa získať takto:

D = (½ V_B²)/(μ_{klimatizovať} . G) = (½ V_B²)/(μ_{klimatizovať} . g) = (½g.h_Do)/(μ_{klimatizovať} . g) = (½h_Do)/μ_{klimatizovať} = 0.5 x 3 m / 0.2 = 7.5 m

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.
2. Figueroa, D. (2005). Séria: Fyzika pre vedu a inžinierstvo. Zväzok 2. Dynamika. Editoval Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. Ed Prentice Hall.
4. Rytier, r.  2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson. 
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1-2.