Helmholtz Free Energy Units, ako sa vypočítava, vyriešené cvičenia

Ten Helmholtzová voľná energia Je to termodynamický potenciál, ktorý meria užitočnú prácu uzavretého systému v podmienkach konštantnej teploty a objemu. Helmholtzova voľná energia je označená ako F A je definovaný ako rozdiel od vnútornej energie Alebo menej teplotný produkt Tón Pre entropiu Siež:

F = u - tells

Pretože ide o energiu, meria sa v jouloch v medzinárodnom systéme (SI), hoci ostatnými vhodnými jednotkami môžu byť Ergios (CGS), kalórie alebo elektrónové volty (EV).

postava 1. Definícia Helmholtzovej energie. Zdroj: Pixabay.

Negatívna variácia Helmholtzovej energie počas procesu sa rovná maximálnej práci, ktorú môže systém vykonávať v izokorickom procese, tj konštantnom objeme. Ak objem nie je konštantný, časť tejto práce sa dá vykonať na životnom prostredí.

V tomto prípade sa odvoláme na prácu, v ktorej sa objem nemení, napríklad elektrická práca: dw = φdq, s φ ako elektrickým potenciálom a q ako elektrický náboj.

Ak je teplota tiež konštantná, Helmholtzova energia sa pri dosiahnutí rovnováhy minimalizuje. Za to všetko je Helmholtzova energia obzvlášť užitočná v procesoch konštantného objemu. V takom prípade máte:

- Pre spontánny proces: ΔF < 0

- Keď je systém v rovnováhe: ΔF = 0

- V nepontánnom procese: ΔF> 0.

[TOC]

Ako sa počíta Helmholtz Free Energy?

Ako sa uvádza na začiatku, Helmholtzova energia je definovaná ako „vnútorná energia alebo systém, s výnimkou produktu systému absolútnej teploty systému, entropickými systémami“:

F = u - tells

Je to funkcia teploty t a objemu V. Kroky na vizualizáciu sú nasledujúce:

Môže vám slúžiť: vnútorné elektróny

- Počnúc prvým zákonom termodynamiky, vnútornou energiou alebo súvisí s entropickými systémami a jeho objemom V pre reverzibilné procesy prostredníctvom nasledujúceho diferenciálneho vzťahu:

du = dq - dw = tds - pdv

Z toho vyplýva, že vnútorná energia alebo je funkciou premenných Siež a Vložka, preto:

U = u (s, v)

- Teraz definícia F A je odvodený:

df = du - d (ts) = du - tds - sdt

- Nahrádza tam diferenciálny výraz získaný pre DU v prvom kroku, zostáva:

Df = tds - pdv - tds - sdt = -sdt - pdv

- Nakoniec sa dospelo k záveru, že F je funkciou teploty t a objemu V a dá sa vyjadriť ako:

F = f (t, v)

Obrázok 2. Hermann von Helmholtz (1821-1894), nemecký fyzik a lekár, uznaný za jeho príspevky k elektromagnetizmu a termodynamike, medzi inými oblasťami vedy. Zdroj: Wikimedia Commons.

Spontánne procesy

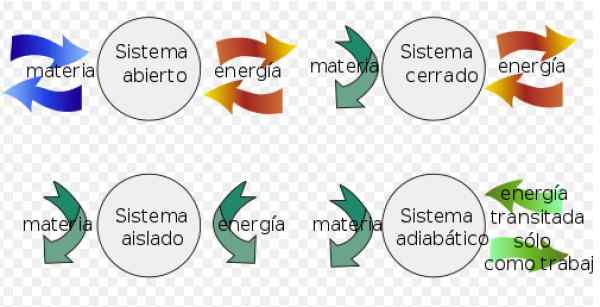
Helmholtzova energia sa dá aplikovať ako všeobecné kritérium spontánnosti v izolovaných systémoch, ale predtým, ako by sa mali špecifikovať niektoré koncepty:

- A zatvorený systém Môže si vymieňať energiu s životným prostredím, ale nemôže si vymeniť záležitosť.

- Namiesto a izolovaný systém nevymieňa si hmotu ani energiu s životným prostredím.

- Konečne a otvorený systém výmenná hmota a energia s životným prostredím. 

Obrázok 3. Termodynamické systémy. Zdroj: Wikimedia Commons. Fjgar (BIS) [CC BY-SA (https: // creativeCommons.Org/licencie/By-SA/4.0)].

V reverzibilných procesoch sa zmeny vnútornej energie vypočítava nasledovne:

DU = TDS - PDV

Teraz predpokladajme proces konštantného objemu (izokorka), v ktorom má druhý termín predchádzajúceho výrazu neplatný príspevok. Treba tiež pamätať na to, že podľa Clausius Nerovnosť: 

DS ≥ DQ/T

Takáto nerovnosť sa vzťahuje na izolovaný termodynamický systém.

Takže pre proces (reverzibilný alebo nie), v ktorom je objem udržiavaný konštanta, je splnená:

Môže vám slúžiť: kyselina fosforečná (H3PO4)

T ds ≥ du (Pri pevnom objeme)

Berúc do úvahy to:

df = du - t ds 

Budeme musieť v izokorickom procese pri konštantnej teplote splniť, že: Df ≤ 0, Ako je uvedené na začiatku.

Takže energia Helmholtz F je v spontánnom procese klesajúce množstvo, zatiaľ čo je to izolovaný systém. F dosiahne svoju minimálnu a stabilnú hodnotu, keď sa dosiahne reverzibilná rovnováha.

Vyriešené cvičenia

Cvičenie 1

Vypočítajte variáciu voľnej energie Helmholtz F pre 2 móly ideálneho plynu pri teplote 300 000 počas izotermálnej expanzie, ktorá vedie k systému počiatočného objemu 20 litrov do konečného objemu 40 litrov.

Riešenie

Počnúc definíciou F:

F = u - t s

Potom bude konečná variácia F, nazývaná AF, bude:

ΔF = ΔU - T ΔS

Ako sa uvádza, že teplota je konštantná: Δt = 0. V ideálnych plynoch však vnútorná energia závisí iba od jej absolútnej teploty, ale keďže ide o izotermálny proces, potom ΔU = 0 a Δf = - t δs. V prípade ideálnych plynov je takto napísaná variácia entropie izotermálneho procesu: 

Δs = n.R.LN (v₂/V₁)

Uplatňovanie tohto výrazu:

ΔS = 2 mol x 8 314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Nakoniec je zmena v Helmholtzovej energii:

Δf = - t δs = - 300k x 11,53 j/k = -3457,70 j.

Cvičenie 2

Vo vnútri valca je piest, ktorý ho rozdeľuje na dve časti a na každej strane piest n móly ideálneho monoatomického plynu, ako je znázornené na obrázku nižšie.

Steny valca sú dobré tepelné vodiče (diatermické) a sú v kontakte s teplotou T teploty T_ani.

Počiatočný objem každej z sekcií valca je V_1i a v_2i, zatiaľ čo jeho posledné zväzky sú V_1F a v_2f Po kvázerskom výtlaku. Piest sa pohybuje pomocou piestom, ktorý hermeticky prechádza cez dva valec tapas.

Môže vám slúžiť: Tecnocio (TC): Štruktúra, vlastnosti, použitia, získanie

Žiada sa, aby ste našli:

a) Zmena vnútornej energie plynu a práce vykonávané systémom a

B) Helmholtzova energetická variácia.

Roztok

Keď sa piest pohybuje kvázneticky, vonkajšia sila aplikovaná na piest musí vyvážiť silu v dôsledku tlakového rozdielu v dvoch častiach valca.

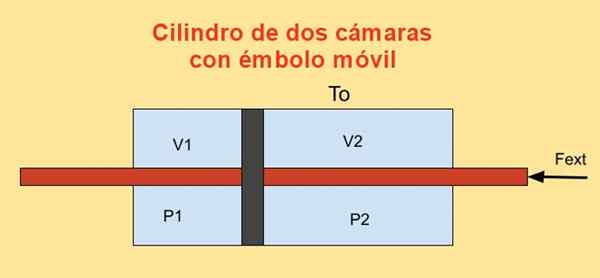Obrázok 4. Variácia voľnej energie F vo valci s dvoma fotoaparátmi. Zdroj: f. Zapata.

Práca Dw Vyrobené externou silou F_rozšíriť počas nekonečného posunu Dx je:

Dw = - f_rozšíriť Dx = (P₁ - P₂) Dx = p₁ DV₁ + P₂ DV₂

Kde sa vzťah použil DV₁ = - dv₂ = Dx, bytosť do Piestová oblasť. Na druhej strane variácia Helmholtzovej energie je: 

Df = -sdt - pdv

Pretože počas procesu sa teplota nemení, potom dt = 0 a Df = - pdv. Aplikácia tohto výrazu na každú časť valca, ktorú máte:

dw = P₁ DV₁ + P₂ DV₂ = - df₁ - Df₂

Bytosť F₁  a F₂ Helmholtzove energie v každej z kamier.

Konečnú prácu W sa dá vypočítať z konečnej variácie Helmholtzovej energie každej kamery:

W = -Af₁ - ΔF₂

Riešenie B

Na nájdenie zmeny energie z Helmholtzu sa používa definícia: F = u - t s. Rovnako ako v každom fotoaparáte máte pri konštantnej teplote ideálny monoatomický plyn Tón_ani, Vnútorná energia sa nemení (ΔU = 0), takže: Δf = - t_ani ΔS. Okrem::

Δs = nr ln (v_F/Píla)

To, že jej nahradením konečne umožňuje vykonanú prácu, je: 

W = -t_ani Nr Ln (v_1F /V_1i) -do nr ln (v_2f /V_2i) = -Af₁ -ΔF₂

W = - až nr ln [(v_1F ⋅ V_1i)/(V_{2f .}Vložka_2i)] = - δf_Celkom

Bytosť ΔF_Celkom Celková variácia Helmholtzovej energie.

Odkazy

1. Castaños e. Bezplatné energetické cvičenia. Získané z: Lidiaconlachimica.Slovník.com
2. Librettexts. Helmholtz Energy. Získané z: Chem.Librettexts.orgán
3. Librettexts. Čo sú bezplatná energia. Získané z: Chem.Librettexts.orgán
4. Wikipedia. Helmholtz Energy. Obnovené z: je.Wikipedia.com
5. Wikipedia. Helmholtzová voľná energia. Zdroj: In.Wikipedia.com