Fyzický

Gravitačné vzorce energie, charakteristiky, aplikácie, cvičenia

Gravitačné vzorce energie, charakteristiky, aplikácie, cvičenia

Ten Gravitačná energia Je to ten, ktorý má masívny objekt, keď je ponorený do gravitačného poľa, ktorý produkuje iný. Niektoré príklady predmetov s gravitačnou energiou sú: jablko v strome, padanie jablka, mesiac obiehajúcich zemou a zemou obiehajúcou slnkom.

Isaac Newton (1642-1727) bol prvým, kto si uvedomil, že gravitácia je univerzálny fenomén a že každý objekt s hmotnosťou vytvára vo svojom prostredí pole schopné produkovať jednu silu na druhú.

postava 1. Mesiac obiehajúci Zem má gravitačnú energiu. Zdroj: Pixabay

[TOC]

Vzorce a rovnice

Sila uvedená v Newtone je známa ako gravitačná sila a poskytuje energiu objektu, na ktorom pôsobí. Newton sformuloval zákon o univerzálnom gravitácii takto:

„Buďte dvoma špecifickými hmotnými objektmi M1 a M2, každý z nich vyvíja silu príťažlivosti, ktorá je úmerná produktu ich hmotností a nepriamo úmerná štvorcovi vzdialenosti, ktorá ich oddeľuje.“.

V predchádzajúcom výraze, F Je to sila gravitačnej príťažlivosti, že Object 1 vyvíja objekt 2 (alebo naopak), M1 a m2 Príslušné hmotnosti objektov a r je vzdialenosť, ktorá oddeľuje objekty. G Je to konštanta proporcionality známa ako gravitačná konštanta.

Gravitačná energia Alebo spojené s gravitačnou silou F je:

Všimnite si prítomnosť negatívneho znamenia, čo znamená, že ak je oddelenie medzi objektmi konečné, jej gravitačná energia je negatívna. Ale ak separácia má tendenciu k nekonečnu, potom je gravitačná energia nula.

Objekt, ktorý je ponorený do gravitačného poľa, má gravitačnú potenciálnu energiu Alebo a kinetická energia Klimatizovať. Ak neexistujú žiadne ďalšie interakcie alebo majú zanedbateľnú intenzitu, celková energia A Z tohto objektu je súčet jeho gravitačnej energie plus jej kinetická energia:

E = k + u

Ak je objekt v gravitačnom poli a nie sú prítomné iné disipatívne sily, napríklad trenie alebo odolnosť proti vzduchu, potom celková energia A Je to množstvo, ktoré zostáva počas pohybu konštantné.

Charakteristiky gravitačnej energie

- Objekt má gravitačnú potenciálnu energiu, ak je iba v prítomnosti gravitačného poľa produkovaného iným.

- Gravitačná energia medzi dvoma objektmi rastie, pretože vzdialenosť medzi nimi je väčšia.

- Práca vykonaná gravitačnou silou je rovnaká a je v rozpore so zmenou gravitačnej energie konečnej polohy vzhľadom na prácu jej pôvodnej polohy.

Môže vám slúžiť: Aká je rovnováha častíc? (S príkladmi)

- Ak je telo vystavené iba pôsobeniu gravitácie, potom je variácia jej gravitačnej energie rovnaká a je v rozpore s variáciou jej kinetickej energie.

- Potenciálna energia hromadného objektu m vo výške h Pokiaľ ide o zemský povrch Mgh časy väčšie ako potenciálna energia na povrchu g zrýchlenie gravitácie pre výšky h Oveľa nižšie ako suchozemský polomer.

Poľný a gravitačný potenciál

Gravitačné pole g Je definovaná ako gravitačná sila F na jednotku hmotnosti. Je určená umiestnením testovacej častice v každom bode priestoru a výpočtom kvocientu medzi silou, ktorá pôsobí na testovaciu častice vydelenú hodnotou jej hmoty:

g = F / m

Gravitačný potenciál V z hromadného objektu M ako gravitačnej potenciálnej energie tohto objektu vydelený jeho vlastnou hmotnosťou je definovaný.

Výhodou tejto definície je, že gravitačný potenciál závisí iba od gravitačného poľa, takže akonáhle je potenciál známy Vložka, Gravitačná energia Alebo hromadného objektu m je:

U = m.Vložka 

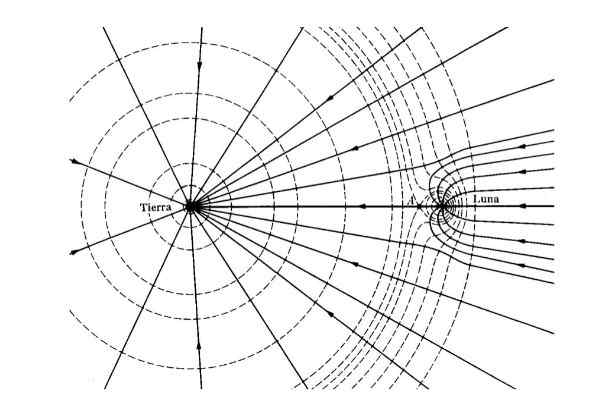Obrázok 2. Gravitačné pole (kontinuálne čiary) a rovnocenné (segmentované riadky) pre systém Zeme - Luna. Zdroj: W T Scott, som. J. Fyzický. 33, (1965).

Žiadosti

Gravitačná potenciálna energia je to, čo telá ukladajú, keď sú v gravitačnom poli.

Napríklad voda obsiahnutá v nádrži má viac energie do tej miery, že nádrž je vyššia výška.

Pri vyššej nádrži, čím väčšia rýchlosť výstupu vody pri kohútiku. Je to preto, že potenciálna energia vody vo výške nádrže sa na výstupe z kohútika transformuje na kinetickú vodnú energiu.

Keď je voda poškodená na vrchole hory, táto potenciálna energia sa môže použiť na otáčanie turbín na výrobu elektrickej energie.

Gravitačná energia tiež vysvetľuje príliv. Pretože energia a gravitačná pevnosť závisí od vzdialenosti, gravitačný ťah Mesiaca je väčší tvárou v tvár zemi najbližšie k Mesiacu ako najvzdialenejšia a najviac opačná tvár.

To spôsobuje rozdiel v silách, ktoré deformujú morskú hladinu. Účinok je väčší na nový mesiac, keď sú slnko a mesiac zarovnané.

Možnosť budovania priestorových a satelitných staníc, ktoré zostávajú relatívne blízko našej planéty, je spôsobená gravitačnou energiou produkovanou Zemou. Ak nie, vesmírne stanice a umelé satelity by sa putovali cez vesmír.

Môže vám slúžiť: IMANTÁCIA: Čo pozostáva, metóda a príklady

Gravitačný potenciál Zeme

Predpokladajme, že Zem má hmotu M a objekt, ktorý je nad zemským povrchom na diaľku r Pokiaľ ide o jeho centrum, má hmotnosť m. 

V tomto prípade je gravitačný potenciál určený z gravitačnej energie, ktorá sa jednoducho rozdelí medzi hmotnosť objektu, ktorá je výsledkom:

Gravitačný potenciál na zemskom povrchu sa získava nahradením r S pozemským polomerom rTón. 

Potenciálna energia v blízkosti zemského povrchu

Predpokladajme, že Zem má rádio RTón  a hmotnosť M.

Aj keď Zem nie je včasným objektom, pole na jeho povrchu je rovnocenné s tým, čo by sa získalo, ak by sa všetka jej hmota M Koncentrovala sa v strede, takže gravitačná energia objektu vo výške h na zemskom povrchu je 

U (rTón + h) = -G.M m (rTón + h)^-1

Ale pretože H je oveľa menší ako rTón, Predchádzajúci výraz sa môže priblížiť 

U = uo + mgh

Kde g je zrýchlenie gravitácie, ktorej priemerná hodnota pre Zem je 9.81 m/s^2.

Potom potenciálne EP EP EP hmotnosti m vo výške h na zemskom povrchu je:

EP (h) = u +uo = mgh

Na zemskom povrchu h = 0, takže objekt na povrchu má ep = 0. Podrobné výpočty je možné vidieť na obrázku 3.

Obrázok 3. Gravitačná potenciálna energia vo výške H na povrchu. Zdroj: Pripravený F. Zapata.

Cvičenia 

Cvičenie 1: Gravitačná Zem

Predpokladajme, že naša planéta trpí gravitačným kolapsom straty tepelnej energie vo vnútri a jej polomer sa rozpadá až do polovice súčasnej hodnoty, ale hmotnosť planéty je konštantná.

Zistite, aké by bolo zrýchlenie gravitácie v blízkosti povrchu novej krajiny a koľko pozostalého váži 50 kg-f pred kolapsom. Zvyšuje alebo znižuje gravitačnú energiu osoby a v akom faktor.

Riešenie

Zrýchlenie gravitácie na povrchu planéty závisí od jej hmoty a jej polomeru. Gravitačná konštanta je univerzálna a slúži rovnako pre planéty a exoplanety.

V prípade, že sme zdvihnutí, ak sa polomer Zeme zníži na polovicu, potom by zrýchlenie závažnosti novej krajiny bolo 4 -krát väčšie. Podrobnosti je možné vidieť na ďalšej doske.

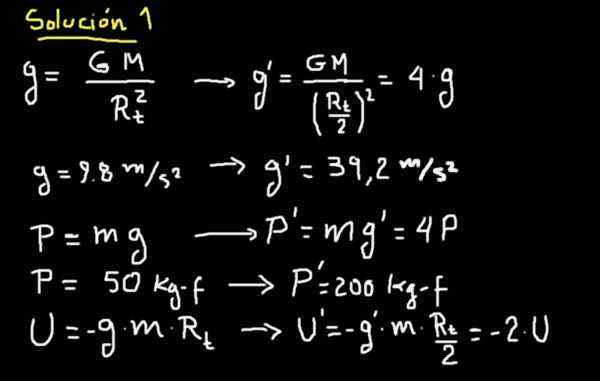
To znamená, že Superman a pozostalý, ktorý na starej planéte vážil 50 kg-f, váži 200 kg-f na novej planéte.

Môže vám slúžiť: tepelná rovnováha: rovnice, aplikácie, cvičenia

Na druhej strane sa gravitačná energia zníži o polovicu na povrchu novej planéty.

Cvičenie 2: gravitačný kolaps a rýchlosť úniku

Pokiaľ ide o situáciu zvýšenú v cvičení 1, čo by sa stalo s rýchlosťou výfukových plynov: zvyšuje sa, znižuje sa, v akom faktore?

Riešenie 2

Rýchlosť výfukových plynov je minimálna rýchlosť potrebná na uniknutie gravitačnej príťažlivosti planéty.

Na jeho výpočet sa predpokladá, že projektil, ktorý strieľa touto rýchlosťou, dosahuje nekonečno nulovou rýchlosťou. Okrem toho je gravitačná energia nekonečna nula. Preto projektil, ktorý strieľa s rýchlosťou výfukových plynov, bude mať nulovú celkovú energiu.

To znamená, že na povrchu planéty v čase výstrelu musí byť súčet kinetickej energie projektilu + gravitačná energia neplatný:

½ m ve^2 - (g m.PánTón = 0

Všimnite si, že rýchlosť výfukových plynov nezávisí od cesta projektilu a jeho štvorcovej hodnoty je

Ve^2 = (2g m) / rTón

Ak sa planéta zrúti až do polovice polomeru originálu, štvorec novej rýchlosti výfuku sa stane dvojnásobkom.

Preto nová rýchlosť výfukových plynov rastie a stáva sa 1.41 -krát starú rýchlosť úniku:

Ve '= 1.41 Pozri

Cvičenie 3: Gravitačná energia Apple

Chlapec na balkóne budovy 30 metrov od zeme vydáva jablko 250 g, ktoré po niekoľkých sekundách dosiahne zem.

Obrázok 4. Pri páde sa potenciálna energia jablka transformuje na kinetickú energiu. Zdroj: Pixabay.

a) Aký je gravitačný energetický rozdiel jablka v hornej časti jablka na úrovni pôdy?

b) ako rýchlo sa jablko pred šírením na zemi?

c) A čo energia, keď sa jablko rozdrví na zem? 

Riešenie

a) Rozdiel v gravitačnej energii je 

m.g.H = 0.250 kg * 9.81 m/s^2 * 30 m = 73.6 J

b) Potenciálna energia, ktorú mal jablko, keď bola vysoká 30 m, sa transformuje na kinetickú energiu, keď jablko dosiahne zem.

½ m v^2 = m.g.h

V^2 = 2.g.h

Nahradením hodnôt a zúčtovaním z toho vyplýva, že jablko dosiahne zem rýchlosťou 24.3 m/s = 87.3 km/h.

c) Zrejme je jablko rozptýlené a všetka gravitačná energia nahromadená na začiatku sa stratí vo forme tepla, pretože kusy jabĺk a zóna nárazu sa zahrievajú, okrem toho sa časť energie rozpúšťa aj vo forme zvukových vĺn "Splash".

Odkazy

  1. Alonso, m. (1970). Fyzika zväzku. 1, Inter -American Educational Fund. 
  2. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5. Edimatizovať. Pearson.
  3. Rytier, r. 2017. Fyzika pre vedcov a inžinierstvo: Strategický prístup. Pearson.
  4. Sears, f. (2009).University Physics Zv. 1 
  5. Wikipedia. Gravitačná energia. Obnovené z: je.Wikipedia.com
  6. Wikipedia. Gravitačná energia. Zdroj: In.Wikipedia.com