ENEGON VLASTNOSTI, Ako vyrobiť engon, príklady

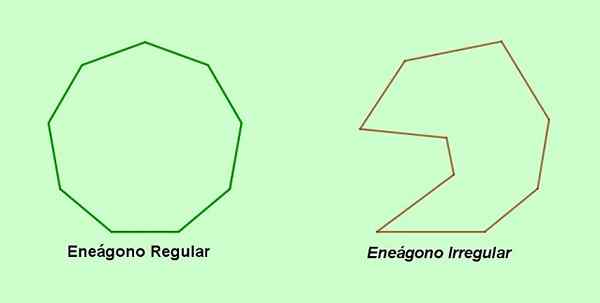
A Engon Je to polygón deviatich strán a deviatich vrcholov, ktoré môžu byť pravidelné alebo nie. Označovanie ENEGON pochádza z gréčtiny a pozostáva z gréckych slov Ennea (deväť a Gonón (uhol).

Alternatívny názov pre deväť -vedený polygón je slovo bez slov, ktoré pochádza z latinčiny nonus (deväť a Gonón (vrchol). Na druhej strane, ak sú boky alebo uhly engonu navzájom nerovnaké, potom je tu a nepravidelný engon. Ak je naopak, deväť strán a deväť uhlov Engonu sú rovnaké, potom je to pravidelný engon.

postava 1. Pravidelný engon a nepravidelný engon. (Vlastné rozpracovanie)

[TOC]

Vlastnosti ENEGON

Pre polygón N strany je súčet jeho vnútorných uhlov:

(N - 2) * 180 °

V engone by to bolo n = 9, takže súčet jeho vnútorných uhlov je:

SA = (9 - 2) * 180 ° = 7 * 180 ° = 1260 °

V akomkoľvek mnohouholníku je počet diagonálov:

D = n (n - 3) / 2 a v prípade Engonu, ako n = 9, musíte d = 27.

Pravidelný engon

V Egone alebo pravidelnom nonagone.

Potom je potrebné zmerať vnútorné uhly engonu 1260 ° / 9 = 140 °.

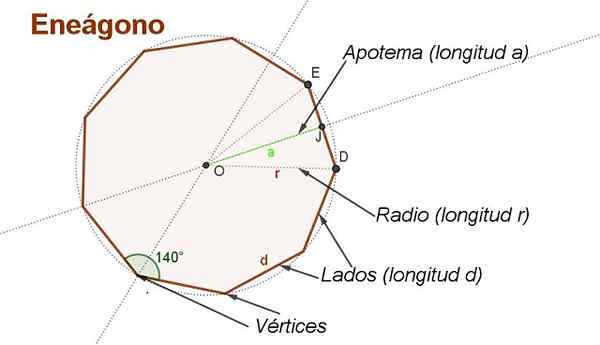Obrázok 2. Apothém, rádio, boky, uhly a vrcholy pravidelného engonu. (Vlastné rozpracovanie)

Odvodiť vzorec oblasti pravidelného Egonu na boku d Je vhodné vytvoriť niektoré pomocné konštrukcie, ako sú konštrukcie znázornené na obrázku 2.

Centrum je Ani Kreslenie mediácií dvoch susedných strán. Stred Ani Equidista vrcholov.

Polomer dĺžky r Je to segment, ktorý prechádza zo stredu Ani Vo vrchole Engonu. Rádiá sú znázornené na obrázku 2 Odplaziť a Oe dĺžka r.

Môže vám slúžiť: symetria

Apotém je segment, ktorý prechádza zo stredu do stredu na jednej strane engonu. Napríklad Oj Je to apothém, ktorého dĺžka je do.

Oblasť známej strany Engon a apothém

Považujeme trojuholník Óda Z obrázku 2. Oblasť tohto trojuholníka je produktom jeho základne Z výškou Oj vydelené 2:

Oblasť Óda = (Od * OJ) / 2 = (D * a) / 2

Pretože v Egone je 9 trojuholníkov tej istej oblasti, dospelo sa k záveru, že jeho oblasť je:

Engon = (9/2) (d * a)

Plocha známeho engonu

Ak je známa iba dĺžka engonu, potom je potrebné nájsť dĺžku apothému, aby bolo možné použiť vzorec predchádzajúcej sekcie.

Považujeme trojuholník Area Obdĺžnik J (Pozri obrázok 2). Ak sa použije trigonometrický pomer krútiaceho momentu, získa sa:

tak (∡Oej) = Oj / Napr.

Uhol ∡eej = 140 ° / 2 = 70 °, za to, že by ste Eo Bisektor vnútorného uhla engonu.

Okrem, Oj Je to apothém dĺžky do.

Potom J Je to stred Edimatizovať To z toho vyplýva Ex = d/2.

Nahradenie vyššie uvedených hodnôt vo vzťahu Tangent je:

Opálenie (70 °) = A / (d / 2).

Teraz vymažeme dĺžku apothémie:

A = (d/2) Opálenie (70 °).

Predchádzajúci výsledok sa nahradí vo vzorci oblasti na získanie:

Engon = (9/2) (d * a) = (9/2)( D * (d/2) Opálenie (70 °))

Nakoniec existuje vzorec, ktorý umožňuje získanie pravidelnej oblasti Engonu, ak je známa iba dĺžka d z jeho strán:

Engon = (9/4) D² Opálenie (70 °) = 6 1818 d²

Obvod pravidelného engonu pozná svoju stranu

Obvod polygónu je súčet jeho strán. V prípade Engonu, rovnako ako každá zo strán, meria dĺžku d, Jeho obvod bude suma deväťkrát d, to znamená:

Môže vám slúžiť: polynómové rovnice

Obvod = 9 d

Obvod Engonu známe jeho rádio

Vzhľadom na trojuholník Area Obdĺžnik J (Pozri obrázok 2), trigonometrický dôvod sa používa Cosen:

cos (∡Oej) = Napr / Oe = (d / 2) / r

Kde si získaš:

D = 2r cos (70 °)

Nahradením tohto výsledku sa obvodový vzorec získava ako funkcia polomeru Engon:

Obvod = 9 d = 18 R cos (70 °) = 6 1564 r

Ako vyrobiť pravidelný engon

1- Na vybudovanie pravidelného Egonu s pravidlom a kompasom je založená na obvode c ktorý ohraničuje Engon. (Pozri obrázok 3)

2- Dve kolmé čiary sa nakreslia stredom alebo obvodom. Potom križovatky A a B jednej z riadkov sú označené obvodom.

3- s kompasom, vďaka čomu je stred v odpočúvaní B a otvorenie rovný polomeru bo.

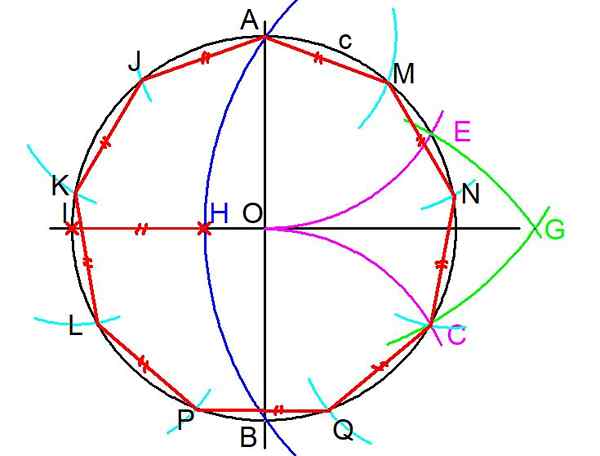Obrázok 3. Kroky na vybudovanie pravidelného engonu. (Vlastné rozpracovanie)

4- Predchádzajúci krok sa opakuje, ale vytváranie centra v a a rádio ao oblúku je nakreslené, ktoré zachytí obvod C v bode e.

5- s otvorením striedavého prúdu a stredom v obvode je nakreslené. Podobne s otvorením BE a Stred B je nakreslený ďalší oblúk. Križovatka týchto dvoch oblúkov je označená ako g.

6- Centrum v G a s otvorením GA sa nakreslí oblúk, ktorý zachytí sekundárnu os (v tomto prípade horizontálne) v bode H. Križovatka sekundárnej osi je označená pôvodným obvodom C ako i.

7- Dĺžka segmentu IH sa rovná dĺžke d na boku ENEGON.

8- s otvorením kompasu IH = d Centrum Arches sú postupne priťahované do rádiu AJ, Centro J Radio AK, KL Radio KL a Centro L Radio LP.

Môže vám slúžiť: lineárne transformácie: Vlastnosti, aké sú použitie, typy, príklady

9- Podobne, počnúc od A a na pravej strane, sú rádiové oblúky ih = d nakreslené z pôvodných obvodov C bodov M, N, C a Q.

10- Nakoniec sú nakreslené segmenty AJ, JK, KL, LP, AM, MN, NC, CQ a nakoniec PB.

Je potrebné poznamenať, že metóda výstavby nie je úplne presná, pretože je možné overiť, že posledná strana PB je o 0,7% dlhšia ako ostatné strany. K dnešnému dňu nie je známa metóda výstavby konštrukcie a kompasu, ktorá je 100% presná metóda.

Príklady

Niektoré vyriešené príklady budú riešené nižšie.

Príklad 1

Chcete postaviť pravidelný engon, ktorého strany merajú 2 cm. Aké rádio by malo mať obvod, ktorý ho ohraničuje, takže pri aplikácii skôr opísanej konštrukcie sa získa požadovaný výsledok?

Riešenie:

V predchádzajúcej časti sa odvodil vzorec, ktorý sa týka polomeru R ohraničeného obvodu s pravidelným Dégonom D:

D = 2r cos (70 °)

Vymazanie r z predchádzajúceho výrazu, ktorý máme:

R = d / (2 cos (70 °)) = 1 4619 * d

Výmena hodnoty d = 2 cm v predchádzajúcom vzorci sa získa polomer 2,92 cm.

Príklad 2

Koľko stojí oblasť pravidelného 2 cm bočného engonu?

Riešenie:

Ak chcete odpovedať na túto otázku, musíte sa odvolať na vzorec, ktorý bol predtým demonštrovaný, ktorý vám umožní nájsť oblasť engonu známeho dĺžky d na jej boku:

Engon = (9/4) D² Opálenie (70 °) = 6 1818 d²

Výmena D pre jeho hodnotu 2 cm v prednom vzorec sa získa:

Engon = 24,72 cm

Odkazy

1. C. A. Do. (2003). Elementy geometrie: s cvičeniami a geometria kompasu. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Redakčná skupina Patria.
3. Oslobodený, k. (2007). Objavovať polygóny. Benchmark vzdelávacia spoločnosť.
4. Hendrik, v. (2013). Zovšeobecnené polygóny. Birkhäuser.
5. Iger. (s.F.). Matematika Tacaná. Iger.
6. Jr. Geometria. (2014). Polygóny. Lulu Press, Inc.
7. Miller, Heeren a Hornsby. (2006). Matematika: uvažovanie a aplikácie (desiate vydanie). Pearson Vzdelanie.
8. Patiño, m. (2006). Matematika 5. Redakčný progreso.