V akých situáciách sú lineárne a kvadratické funkcie?

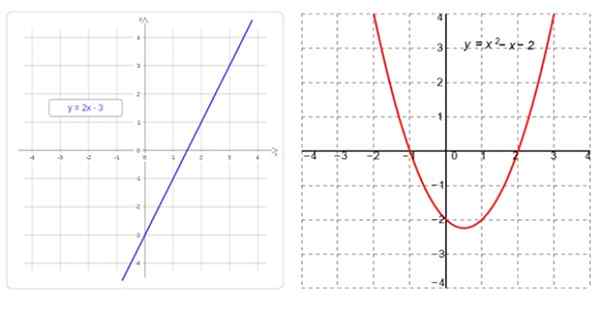
Vľavo je lineárna funkcia, ktorej graf je priamka a napravo, kvadratická funkcia, ktorej graf je parabola. Zdroj: f. Zapata

Čo sú lineárne a kvadratické funkcie?

Lineárne funkcie a kvadratické funkcie sú funkcie, ktoré patria do skupiny polynomických funkcií. Používajú sa na modelovanie rôznych situácií, ako je závislosť medzi objemom a hmotnosťou tela, množstvom a nákladmi na produkt, polohou verzus čas a viac.

Všeobecne platí, že funkcia je vzťah, ktorý spája dve premenné a dá sa použiť na modelovanie skutočného sveta. Polynomické funkcie, ako už názov napovedá, sa vyjadrujú prostredníctvom polynómu, ktorého všeobecná forma je:

f (x) = a_nXⁿ + do _N-1X ^N-1 + do_X-2X^N-2 +.._ani

Kde n je prirodzené číslo, čísla₀, do₁, do₂,.._n Sú skutoční, do₀ Je to nezávislý termín a_n, Je to koeficient, ktorý sprevádza najvyššiu silu. Hodnota n označuje typ funkcie, pre n = 1 je funkcia lineárna, zatiaľ čo pre n = 2 je funkcia kvadratická.

V prvom z týchto prípadov sa všeobecný výraz zníži na:

f (x) = a₁x + a_ani

A v druhom prípade zostáva takto:

f (x) = a₂X² + do₁x + a_ani ;   (₂≠ 0)

Grafy polynómových funkcií sú nepretržité, to znamená, že nezažívajú náhle skoky alebo prasknutia, takže majú mäkké správanie bez nezrovnalostí. Preto sú pozorované pri modelovaní mnohých situácií vedy, ekonómie a iných oblastí ľudských znalostí.

Ďalej sú podrobnejšie opísané zaujímavé aplikácie.

Situácie, v ktorých sa objavujú lineárne funkcie

Lineárna funkcia je reprezentovaná algebraicky podľa:

f (x) = a₁x + a_ani

Alebo ekvivalentne:

f (x) = mx + b

Jeho výraznou vlastnosťou je, že jeho graf je priamka. Hodnota m, čo je koeficient X, predstavuje náušnica tejto línie a dáva mieru toho, ako je naklonená.

Môže vám slúžiť: nelineárne programovanie: metódy a cvičenia

Sklon môže byť kladný, záporný alebo nula, ale je vždy konštantný, to znamená, že jeho výmenný kurz zostáva nezmenený.

Čiara sklonu 0 je úplne vodorovná, línia kladného sklonu naznačuje zvýšenie alebo zvýšenie (ak sa jedna z premenných zvyšuje, druhá tiež, vždy rovnakou rýchlosťou) a nakoniec, záporný sklon naznačuje pokles (ako A premenných Zvyšuje sa, ďalšie klesá).

Hodnota b, Pokiaľ ide o svoju časť, predstavuje rez alebo priesečník čiary s vertikálnou osou. Jo B = 0, Čiara prechádza pôvodom súradníckeho systému.

Príklady modelovania s lineárnymi funkciami

1. Rovnomerný priamy pohyb

Rovnica, ktorá spája polohu X a čas t mobilu v rovnomernom priamom pohybe, je lineárna:

x (t) = v⋅t + x_ani

Kde v, sklon čiary, je rýchlosť mobilu, ktorý zostáva konštantný počas celého pohybu, a x_ani je počiatočná poloha.

2. Hustota

Hustota objektu alebo látky, ktorá vytvára vzťah medzi hmotnosťou a objemom. Volá ρ na hustotu (znie „rho“), m na cesto a v do hlasitosti, máte:

Vymazanie cesta, pokiaľ ide o objem, získa sa:

M = ρv

Pri grafu cesta v závislosti od objemu sa získa priama čiara, ktorej sklon je hustota objektu alebo látky.

3. Obvod

Obrys kruhu alebo jeho dĺžky je úmerný jeho polomeru. To znamená, že čím väčší polomer, tým väčší obrys obvodu podľa rovnice:

Môže vám slúžiť: korelačný koeficient: vzorce, výpočet, interpretácia, príklad

C = 2πr

Kde C je obrys alebo dĺžka, R je rádio a π (číta „pi“) konštanta, ktorej približná hodnota je πamp3.14 ..

4. Náklady na odosielanie balíka

Ako je ľahké odvodiť, ťažší alebo objemný je drahší balík na jeho prepravu. Spoločnosti, ktoré sa venujú modelu nákladu prepravy svojich cien podľa určitých pravidiel, napríklad:

C (x) = 2.75x

V tejto rovnici sú C (x) náklady na odoslanie balíka, ktorého hmotnosť je x libry. Konštantná hodnota 2.75 má jednotky dolára/libry (jednotkové náklady).

Situácie, v ktorých sa objavujú kvadratické funkcie

Algebraicky je kvadratická funkcia reprezentovaná:

f (x) = a₂ X² + do₁ x + a_ani

S podmienkou, ktoré koeficient₂ Byť odlišný od 0. Vyznačuje sa jej grafom s parabolom, ktorého os axiálnej os alebo os symetrie je vertikálna (rovnobežná s osou y))))).

Križovatka medzi podobenstvom a uvedenou osou je bod nazývaný vrchol. Ak sa podobenstvo otvára (a₂ > 0), vrchol je jeho minimálny bod, a ak sa otvorí (a₂ < 0), es el máximo.

Na osi symetrie je zameranie, špeciálny bod, ktorý určuje zakrivenie paraboly. Ak je na parabolickom zrkadle ovplyvnené slnečné svetlo, lúče sa odrazia na povrchu, čo sa zhoduje v zaostrení, ktorý sa okamžite zahrieva.

Príklady modelovania s kvadratickými funkciami

1. Výška projektilu spusteného vertikálne nahor

Projektil je akýkoľvek objekt, ku ktorému je poskytnutá a uvoľnená počiatočná rýchlosť, pod akciou gravitácie. Ak je počiatočná rýchlosť zvislá, veľkosť V₀ a nasmerovaný nahor, objekt sa zvýši na maximálnu výšku a potom zostúpi.

Môže vám slúžiť: homotecia

Rovnica výšky H ako funkcia času t je:

H (t) = −4.9 t²+vložka₀ tón

Kde sa vertikálny zmysel považuje za pozitívny a vertikálny dole negatívny.

2. Trajektória horizontálneho alebo šikmého projektilu

Ak je projektilu poskytnutá horizontálna alebo šikmá počiatočná rýchlosť, opíše parabolickú trajektóriu, ktorá môže byť reprezentovaná prostredníctvom kvadratickej funkcie, ako už bolo opísané.

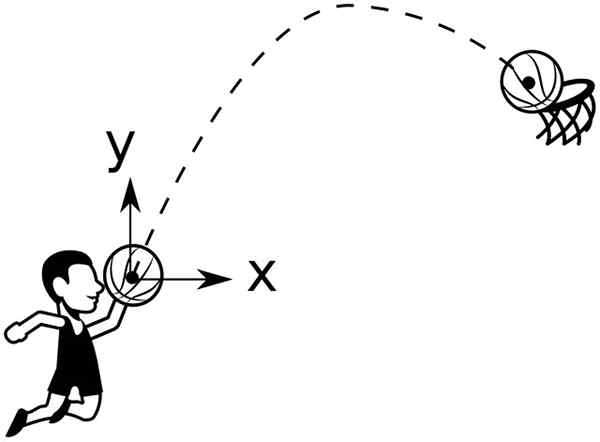Kôšova guľa popisuje parabolickú trajektóriu, ktorá sa má hodiť do koša. Zdroj: Wikimedia Commons

Napríklad lopta vyhodená z výšky a₀, formujúci uhol 9₀ Pokiaľ ide o vodorovné, má trajektóriu danú:

S g ako zrýchlenie gravitácie, ktoré sa môže približovať 10 m/s². Napríklad futbalový lopta kop zo zeme (a₀ = 0), s počiatočnou rýchlosťou 6 m/s a uhlom 45 ° vzhľadom na vodorovné, bude mať trajektóriu danú podľa nasledujúceho podobenstva:

3. Oblasť kruhu

Čím vyšší je polomer kruhu, tým väčšia bude jeho oblasť. Oblasť kruhu je skutočne úmerná štvorcovi polomeru R, konštanta proporcionality je číslo π:

A = πr²

4. Účinnosť reklamy

Čím viac to vidia, tým efektívnejšia je komerčná reklama. Účinnosť e, na stupnici od 0 do 10, je možné modelovať podľa nasledujúcej kvadratickej funkcie:

Odkazy 

1. Polynomické funkcie. Získané zo zdrojov.vzdelávanie.je.
2. Larson, R. (2012). Predbežné vyfarbenie. 8. vydanie. Učenie sa.
3. Miller, C. (2013). Matematika: uvažovanie a aplikácie. 12. vydanie. Pearson Vzdelanie.
4. Stewart, J. (2012). Predbežné vyfarbenie. Matematika na výpočet. 6. vydanie. Učenie sa.
5. Zill, D. (2008). Predbežné náskoky s výpočtovými pokrokmi. 4. vydanie. McGraw Hill.