Vzorec rovníc druhého stupňa, ako ich vyriešiť, príklady, cvičenia
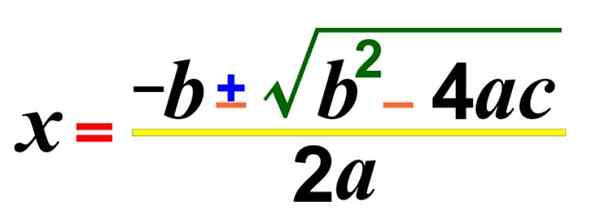
- 1129
- 167
- Václav Višňovský
Ten Druhý stupeň alebo kvadratické rovnice A neznámy má formu sekera2 + BX + C = 0. Kde ≠ 0, od 0, rovnica by sa transformovala na lineárnu rovnicu a koeficienty A, B a C sú skutočné čísla.
Neznámy, ktorý sa má určiť, je hodnota x. Napríklad 3x rovnica2 - 5x + 2 = 0 je úplná rovnica druhého stupňa.
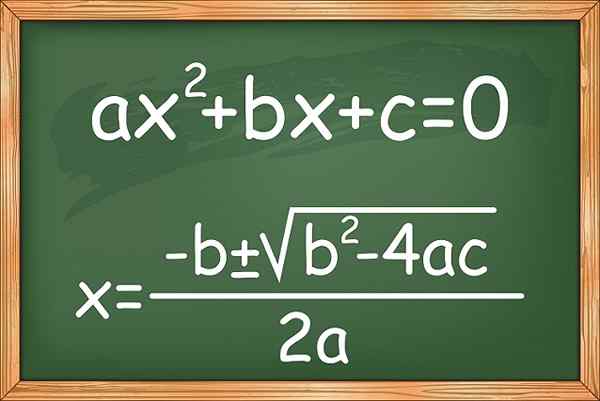 postava 1. Vzorec na riešenie druhého stupňa alebo kvadratické rovnice neznámeho
postava 1. Vzorec na riešenie druhého stupňa alebo kvadratické rovnice neznámeho Existujú aj varianty, ktoré sú známe ako neúplné druhé -degree rovnice, ktoré nemajú niektoré z podmienok, s výnimkou pojmov sekera2. Tu je niekoľko príkladov:
X2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, slávny arabský matematik staroveku, opísaný vo svojich dielach Rôzne typy rovníc prvého a druhého stupňa, ale iba s pozitívnymi koeficientmi. Bola to však francúzsky matematický Rozlíšenie:
Toto je všeobecný vzorec, ktorý umožňuje vyriešiť kvadratickú rovnicu, nájsť korene alebo nuly, aj keď riešenia nie sú skutočné. Existujú aj iné spôsoby, ako ich vyriešiť.
[TOC]
Ako vyriešiť rovnice druhého stupňa?
Druhé degree rovnice možno vyriešiť podľa vyššie uvedeného vzorca a existujú aj ďalšie algebraické postupy, ktoré môžu v niektorých rovniciach pracovať.
Navrhovanú rovnicu vyriešime na začiatku vzorcom, platná metóda pre akúkoľvek rovnicu druhého stupňa s neznámymi:
3x2 - 5x + 2 = 0
Na použitie vzorca správne si všimneme, že:
- do Je to koeficient pojmu s x2
- b Je to koeficient lineárneho termínu
- c je nezávislý termín.
Ideme ich z tej istej rovnice:
A = 3
B = -5
C = 2
Všimnite si, že znak, ktorý sprevádza koeficient, sa musí zohľadniť. Teraz tieto hodnoty nahrádzame vo vzorci:
V čitateľovi je symbol „viac - menej“ ±, čo naznačuje, že množstvo s koreňom sa môže považovať za pozitívne a tiež negatívne. Rovnica druhého stupňa má maximálne dve skutočné riešenia a tento symbol ju zohľadňuje.
Zavolajme x1 a x2 Pre tieto dve riešenia, potom:
X1 = (5+1) / 6 = 1
X2 = (5-1)/6 = 4/6 = 2/3
Rozlíšenie faktorizáciou
Niektoré rovnice druhého stupňa pozostávajú z trinomialov, ktoré sú ľahko faktorom. Ak áno, táto metóda je oveľa rýchlejšia. Zvážte rovnicu:
X2 + 7x - 18 = 0
Faktorizácia má túto formu:
Môže vám slúžiť: Zhoda: zhodné čísla, kritériá, príklady, cvičenia(x +) ⋅ (x -)
Prázdne medzery sú vyplnené dvoma číslami, ktoré, keď sú vynásobené v 18 a keď sa odpočítajú, 7 je 7. Znaky v zátvorkách sú vybrané s týmto kritériom:
-V prvej zátvorke je znamenie medzi prvým a druhým termínom umiestnené.
-A v druhej zátvorke ide produkt príznakov, ktoré sú vidieť.
Pokiaľ ide o čísla, v tomto prípade sú ľahko: sú 9 a 2. Najstarší je vždy umiestnený v prvej zátvorke, ako je tento:
X2 + 7x - 18 = (x + 9). (x - 2)
Čitateľ si môže skontrolovať distribučnú vlastnosť, ktorá pri vývoji produktu pravej strany rovnosti sa získa trinomén ľavice. Teraz je rovnica prepísaná:
(x + 9) ⋅ (x - 2) = 0
Aby sa rovnosť splnila, stačí, aby jeden z týchto dvoch faktorov bol nula. Takže v prvom sa musí urobiť1 = -9 alebo je možné, že druhý faktor je zrušený, v tomto prípade x2 = 2. Toto sú riešenia rovníc.
Grafická metóda
Korene alebo roztoky rovnice druhého stupňa zodpovedajú križovatkám podobenstva y = = sekera2 + BX + C S vodorovnou osou alebo osou x. Takže grafom zodpovedajúceho podobenstva nájdeme riešenie rovnice druhého stupňa, ktoré robia y = 0.
Striky podobenstiev s horizontálnou osou predstavujú roztoky rovnice sekera2 + BX + C = 0. Podobenstvo, ktoré prerezáva iba vodorovnú os v jednom bode, má jediný koreň a vždy to bude vrchol paraboly.
A nakoniec, ak sa podobenstvo neodreže na horizontálnu os, zodpovedajúca rovnica sekera2 + BX + C = 0 Chýba mu skutočné riešenia.
Budovanie ručného grafu môže byť namáhavé, ale s použitím programov, ktoré sú grafom online, je to veľmi jednoduché.
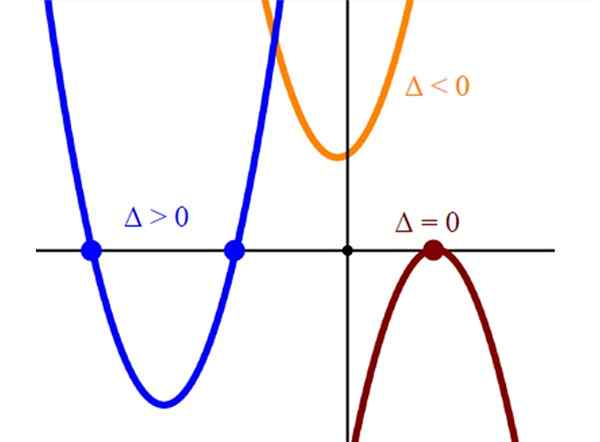 Obrázok 2. Grafické znázornenie troch typov podobenstiev, s dvoma, jedným a žiadnou križovatkou s horizontálnou osou. Zdroj: Wikimedia Commons.
Obrázok 2. Grafické znázornenie troch typov podobenstiev, s dvoma, jedným a žiadnou križovatkou s horizontálnou osou. Zdroj: Wikimedia Commons. Rozlíšenie s vedeckou kalkulačkou
Mnoho modelov vedeckých kalkulačiek má možnosť riešiť rovnice druhého stupňa (a tiež ďalšie typy rovníc). Ak chcete vedieť, musíte skontrolovať ponuku.
Akonáhle je zvolená voľba kvadratickej rovnice neznámeho, ponuka požiada o zadanie hodnôt koeficientov A, B a C a vráťte skutočné riešenia, ak existujú. A existujú aj modely vedeckých kalkulačiek, ktoré pracujú so zložitými číslami a ponúkajú tieto riešenia.
Môže vám slúžiť: násobky 2: Čo sú a vysvetlenieDiskriminácia z rovnice druhého stupňa
Vedieť, či má rovnica skutočné riešenia alebo nie a koľko je, bez toho, aby bolo potrebné vyriešiť najprv, diskriminácia je definovaná ako suma pod druhým druhom koreňa:
Δ = B2 - 4AC
Podľa diskriminačného znamenia je známe, koľko riešení má rovnica podľa tohto kritéria:
-Dve skutočné riešenia: δ> 0
-Skutočné riešenie (alebo dve rovnaké riešenia): δ = 0
-Žiadne skutočné riešenie: δ < 0
Napríklad, koľko riešení má rovnica druhého stupňa -7x2 +12x + 64 = 0? Identifikujeme koeficienty:
A = -7
B = 12
C = 64
Δ = B2 - 4AC = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Rovnica má dve riešenia. Teraz uvidíme tento:
X2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Toto je rovnica s jedinečným riešením alebo s dvoma rovnakými riešeniami.
Príklady jednoduchých rovníc druhého stupňa
Na začiatku sme povedali, že rovnice druhého stupňa by mohli byť dokončené, ak je trinomiál, a neúplný, ak lineárny termín alebo nezávislý termín chýba. Teraz sa pozrime na niektoré konkrétne typy:
X Formova rovnica2 + mx + n = 0
V tomto prípade A = 1 a vzorec sa redukuje na:
Pre tento typ rovnice a vždy v závislosti od zostávajúcich koeficientov môže metóda faktorizácie fungovať dobre, ako sme videli v predchádzajúcej časti.
Neúplná rovnica formulára Ax2 + C = 0
Riešenie, ak existuje, je forma:
Existuje skutočné riešenie, keď A O C má negatívne znamenie, ale ak majú tieto dva výrazy rovnaké znamenie, riešenie bude imaginárne.
Neúplná rovnica formulára Ax2 + Bx = 0
Táto rovnica sa rýchlo vyrieši pomocou faktorizácie, pretože X je spoločným faktorom v oboch výrazoch. Jedným z riešení je vždy x = 0, druhý je taký:
sekera2 + Bx = 0
x (ax + b) = 0
AX + B = 0 → x = -b/a
Pozrime sa potom na príklad. Vyriešiť:
X2 - 5x = 0
x (x - 5) = 0
Preto x1 = 0 a x2 = 5
Rovnice s menovateľom
Existuje niekoľko racionálnych rovníc, v ktorých môže byť neznámy prítomný v čitateľovi aj v menovateľovi, alebo dokonca iba v druhom, a že algebraickými manipuláciami sa redukujú na kvadratické rovnice.
Spôsob, ako ich vyriešiť, je vynásobiť obe strany rovnosti minimálnym bežným násobkom alebo m.c.m menovateľov a potom usporiadať podmienky. Napríklad:
Môže vám slúžiť: Koľko priemerov má obvod?Rovnice vyššieho poriadku, ktoré sa transformujú na kvadratické
Existujú rovnice s vyšším poriadkom, ktoré prostredníctvom premennej zmeny môžu byť vyriešené, akoby boli kvadratické, napríklad táto rovnica Bicadrada:
X4 - 10x2 + 9 = 0
Nech x2 = U, potom sa rovnica zmení na:
alebo2 - 10U + 9 = 0
Táto rovnica je rýchlo vyriešená faktorizáciou, nájdenie dvoch čísel, ktoré sa vynásobia v 9 a pridané 10. Tieto čísla sú 9 a 1:
(U - 9).(U - 1) = 0
Preto riešenia tejto rovnice sú u1 = 9 a u2 = 1. Teraz vrátime zmenu:
X2 = 9 → x1 = 3 a x2 = -3
X2 = 1 → x1 = 1 a x2 = -1
Pôvodná rovnica je v poriadku 4, preto má najmenej 4 korene. Príkladom je -3, -1, 1 a 3.
Jednoduché vyriešené cvičenia
- Cvičenie 1
Vyriešte nasledujúcu kvadratickú rovnicu s neznámym v menovateľovi:
Minimálny násobok je x (x+2) a musí sa vynásobiť všetkým výrazom:
Ekvivalentný výraz zostáva:
5x (x+2) - x = x (x+2)
Vyvíjame:
5x2 + 10x - x = x2 + 2x
Všetky výrazy sú transponované doľava od rovnosti a doprava je vľavo 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Zohľadňujeme, pretože ide o neúplnú rovnicu:
x (4x - 7) = 0
Jedným z riešení je x = 0, druhé je:
4x = 7
x = 7/4
- Cvičenie 2
Nájdite riešenie rovníc druhého stupňa:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Roztok
Z tejto rovnice poznáme determinant A, pretože bol vypočítaný ako príklad predtým, takže ju využijeme, a vyjadrujeme vzorec rozpúšťadla nasledovne:
X1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
X2 = (-12 -44) / -14 = 4
Riešenie B
Štvorcový trinomial x2 - 6x + 9 je faktorizovateľný, pretože je to perfektný štvorcový trinomén:
X2 - 6x + 9 = (x-3)2 = 0
Riešenie tejto rovnice je x = 3.
- Cvičenie 3
Aká je rovnica, ktorej riešenia sú 3 a 4?
Riešenie
Faktorizovaný výraz je:
(x - 3) ⋅ (x - 4) = 0
Uplatňovanie distribučnej vlastnosti:
X2 - 4x -3x + 12 = 0
Dva centrálne termíny sú podobné a môžu sa znížiť, by boli: odchod:
X2 - 7x + 12 = 0
Odkazy
- Plechovka. 1977. Elementárna algebra. Venezuelské kultúrne vydania.
- Hoffman, J. Výber matematických problémov. Zväzok 2.
- Jiménez, r. 2008. Algebra. Sála.
- Stewart, J. 2006. Predbežné vycvičenie: matematika na výpočet. 5. Vydanie. Učenie sa.
- Zapata, f. 4 spôsoby, ako vyriešiť rovnicu druhého stupňa. Získané z: Francesphysics.Blog.com.
- Zill, D. 1984. Algebra a trigonometria. McGraw Hill.
- « Štruktúra polymérov sčítania, charakteristiky, funkcie, použitie
- Vnútorné charakteristiky motivácie a príklady »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)