Všeobecná rovnica čiary, ktorej sklon sa rovná 2/3

Všeobecná rovnica riadku L je nasledovná: Ax+x+c = 0, kde a, b a c sú konštantné, x je nezávislá premenná e a závislá premenná.

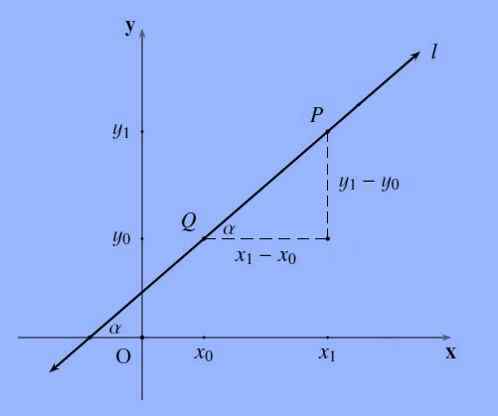
Sklon čiary, označený všeobecne písmenom M, ktorý prechádza bodmi p = (x1, y1) a q = (x0, y0) je nasledujúci kvocient m: = (y1-y0)/(x1 -X0).

Sklon priamky predstavuje sklon; Formálnejšie povedané, sklon čiary je dotyčnica uhla, že tento tvar s osou x.

Je potrebné poznamenať, že poradie, v ktorom sú body pomenované, je ľahostajné, pretože (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Prebiehajúca čiara

Ak sú známe dva body, cez ktoré čiara prechádza, je ľahké vypočítať jeho sklon. Čo sa však stane, ak tieto body nie sú známe?

Vzhľadom na všeobecnú rovnicu riadku AX+x+C = 0 musí byť.

Aká je všeobecná rovnica línie, ktorej sklon je 2/3?

Pretože sklon čiary je 2/3, potom je vytvorená rovnosť -a/b = 2/3, ktorá vidí, že a = -2 a b = 3. Takže všeobecná rovnica čiary so sklonom rovnajúcou sa 2/3 je -2x+3y+c = 0.

Malo by sa objasniť, že ak ste vybraní a = 2 a b = -3, získa sa rovnaká rovnica. Skutočne, 2x -3y+c = 0, čo sa rovná predchádzajúcemu vynásobenému -1. Znak C nezáleží, pretože je to všeobecná konštanta.

Ďalšie pozorovanie, ktoré je možné urobiť, je to, že pre a = -4 a b = 6 sa získava rovnaká čiara, hoci jej všeobecná rovnica je iná. V tomto prípade je všeobecná rovnica -4x+6y+c = 0.

Existujú aj iné spôsoby, ako nájsť všeobecnú rovnicu riadku?

Odpoveď je áno. Ak je známy sklon čiary, existujú dve formy, okrem predchádzajúcej, na nájdenie všeobecnej rovnice.

Na tento účel sa použije bodová rovnica a rezacia rovnica.

-Bodová rovnica: Ak je M sklonom čiary a p = (x0, y0) bodom, kam prechádza, potom sa rovnica y-y0 = m (x-x0) nazýva bodová rovnica, ktorá čaká na bodovú rovnicu.

-Rezacia rovnica: Ak je M sklonom čiary a (0, b) je rez čiary s osou y, potom sa rovnica y = mx+b nazýva rezná rovnica.

Pomocou prvého prípadu sa získa, že bodová rovnica čiary, ktorej sklon je 2/3, je daná výrazom y-y0 = (2/3) (x-x0).

Na dosiahnutie všeobecnej rovnice sa všetky výrazy vynásobia 3 na oboch stranách a sú zoskupené, čím sa získa -2x+3y+(2 × 0-3Y0) = 0 je všeobecná rovnica čiary, kde c = 2 x 0-3Y0.

Ak sa použije druhý prípad, získa sa, že rezná rovnica čiary, ktorej sklon je 2/3, je y = (2/3) x+b.

Opäť platí, že vynásobenie 3 na oboch stranách a zoskupenie všetkých premenných sa získa -2x+3y -3b = 0. Ten je všeobecnou rovnicou riadku, kde c = -3b.

V skutočnosti, pri pohľade na obidve prípady, je možné vidieť, že druhý prípad je jednoducho konkrétnym prípadom prvého (keď x0 = 0).