Diskrétne rozdelenie
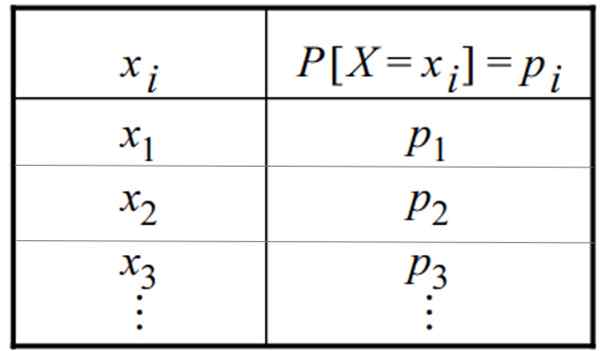
- 2684
- 586
- Denis Škriniar
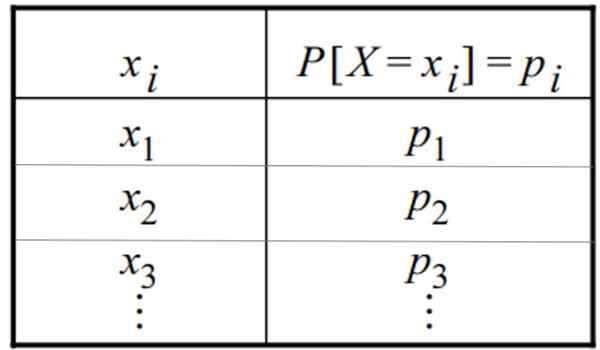 Tabuľka diskrétneho rozdelenia pravdepodobnosti. Zdroj: f. Zapata
Tabuľka diskrétneho rozdelenia pravdepodobnosti. Zdroj: f. Zapata Čo je diskrétna distribúcia?
A distribúcia pravdepodobnosti je funkcia f (xJo), ktorá priraďuje každej hodnote diskrétnej premennej: x1, X2, X3,... XJo, určitý výskyt výskytu p (x = xJo). Táto funkcia je známa aj ako „funkcia hmotnosti pravdepodobnosti“.
Diskrétne rozdelenie pravdepodobnosti môže byť uvedené vo forme tabuľky alebo grafiky. Tabuľka obsahuje túto všeobecnú formu, v ktorej sa premenná objaví v jednom stĺpci a jej príslušná pravdepodobnosť v druhom:
Hmotnostné funkcie pravdepodobnosti zdieľajú tieto všeobecné charakteristiky:
- Pravdepodobnosť PJo akejkoľvek udalosti XJo Je to medzi 0 a 1, dokonca aj niektoré z týchto limitných hodnôt: 0 ≤ x ≤ 1.
- P (x = xJo) = pJo Stačí brať kladné hodnoty, preto: P (x = xJo) ≥ 0.
- Je pravda, že ∑ p (xJo) = 1 pre všetky možné hodnoty x.
Distribúcia pravdepodobností opisuje správanie populácie opísané jej parametrami: priemer μ, rozptyl σ2 a štandardná odchýlka s = σ σ2.
Ďalej sú stručne opísané najvýznamnejšie diskrétne rozdelenie:
Rovnomerné rozdelenie
Je to najjednoduchšie diskrétne rozdelenie všetkých. V nej premenná môže mať „n“ diskrétne hodnoty: x1, X2, X3,... XJo, Všetko s rovnakou pravdepodobnosťou. V tomto prípade je distribúcia daná:
Binomické rozdelenie
Vzťahuje sa na skúsenosti s iba dvoma možnými a vzájomne sa vylučujúcimi výsledkami, ktoré sa zvyčajne nazývajú „úspech“ a „zlyhanie“, označované ako E a F. Skutočnosť, že udalosť sa nazýva „úspech“, nemusí nevyhnutne znamenať, že je to dobrá vec, je to skôr svojvoľné označenie.
Pravdepodobnosť úspechu p (e) pri skúškach „N“ je označená ako p a pravdepodobnosť zlyhania p (f) ako q = 1 - p.
Ak „x“ predstavuje určitý počet úspechov v nezávislých pokusoch „N“, je pravda, že: 0 ≤ x ≤ n. A pravdepodobnosť výskytu p (x) udalosti sa vypočíta prostredníctvom nasledujúceho vzorca:
Môže vám slúžiť: štvorcové centimetre do štvorcových metrov (cm² až m²)Kde x = 0, 1, 2, 3 ..., n a symbol (!) znamená „faktor“:
X! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1
0! = 1
Poisson Distribúcia
V tejto distribúcii náhodná premenná X označuje, koľkokrát sa udalosť vyskytuje v určitom intervale, ktorý môže mať čas, vzdialenosť alebo inú. Výskyty udalosti sú náhodné, nezávislé a sú rozdelené rovnomerne počas daného intervalu.
Akonáhle sú tieto podmienky, pravdepodobnosť, ktorá závisí od priemeru výskytov μ a počtu Eulerov alebo čísla „E“, sa vypočíta podľa:
Šance na udalosti s týmto distribúciou sú malé, preto sa nazýva „zákon zriedkavých prípadov“.
Binomický distribučný prístup
Poissonova distribúcia slúži ako prístup k binomickému rozdeleniu, keď n je veľký (n≥ 100) a P je malý (NP ≤ 10). V tomto prípade sa priemer μ vypočíta ako:
μ = n ∙ P
Hypergeometrická distribúcia
Používa sa, keď pravdepodobnosti nie sú nezávislé, to znamená, že po vykonaní experimentu nie sú podmienky opäť rovnaké. To sa stane pri extrahovaní vzoriek bez náhrady z populácie, takže binomické rozloženie sa už nedá použiť.
Ak populácia pozostáva z dvoch typov objektov odlišných od a B, a pri náhodných objektoch a bez výmeny, pravdepodobnosť získania X objektov typu A sú:
Kde A a B sú príslušné množstvá objektov každého typu, prítomné v populácii.
Ak je však populácia veľmi veľká, aj keď nie je žiadna náhrada, je ťažké, aby bol ten istý prvok vybraný viackrát, takže obe distribúcie: binomické a hypergeometrické, prinesú podobné výsledky.
Môže vám slúžiť: Rozdiel kociek: vzorce, rovnice, príklady, cvičeniaPríklady
Spúšťa sa mince
CO -LAUNCHES sú veľmi ilustratívne príklady:
-Spustenie čestnej meny a získajte tvár. Je známe, že 1 tvár má ½ pravdepodobnosť odchodu a kríž (0 tvár), to isté. Distribúcia je uvedená v tejto tabuľke:
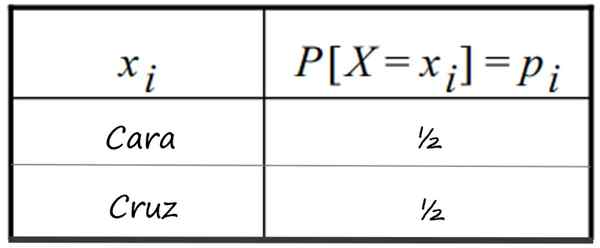 Tabuľka diskrétneho rozdelenia pravdepodobnosti, ktorá nasleduje po spustení 1 čestnej meny. Zdroj: f. Zapata
Tabuľka diskrétneho rozdelenia pravdepodobnosti, ktorá nasleduje po spustení 1 čestnej meny. Zdroj: f. Zapata -Súčasný záber dva čestné mince a možné čísla tváre, ktoré je možné získať.
 Tabuľka diskrétnej distribúcie pravdepodobnosti, ktorá sleduje spustenie dvoch čestnej meny s cieľom získať akúkoľvek tvár alebo nie. Zdroj: f. Zapata
Tabuľka diskrétnej distribúcie pravdepodobnosti, ktorá sleduje spustenie dvoch čestnej meny s cieľom získať akúkoľvek tvár alebo nie. Zdroj: f. Zapata Premenné s rovnomerným rozdelením
-Výber celočíselného čísla, ktoré je rovnomerné alebo nepárne.
-Spustenie čestných kocky. V tomto prípade existuje 6 očíslovaných tvárí a každá z nich má rovnakú pravdepodobnosť odchodu: 1/6.
-Výber témy, ktorá sa má zúčastniť skúšky, vybraná z problémov medzi N, ak sú všetky rovnako pravdepodobné.
Premenné s binomickým rozdelením
-Počet tvárí, ktoré vyjdú spustením čestnej mince.
-Z populácie 250 rodín, počet z nich, ktoré majú 2 deti.
-Množstvo ružových drevín, ktoré prežijú, po záhradníkovi 20 Rosales v záhrade.
-Štúdie s 50 pacientmi, počet z nich, ktorý predstavoval negatívnu reakciu na liek.
-Počet študentov schválených na skúške pravdepodobnosti skupiny zloženej zo 100 študentov.
Premenné s Poissonovou distribúciou
-Počet hovorov za minútu Call centrum Spoločnosť.
-Počet veľkých zemetrasení ročne pre konkrétnu geografickú oblasť.
-Počet tornád, ktoré v poslednom roku ovplyvnili určitý región.
-Počet stromov infikovaných hubou na štvorcový hektár lesa.
Premenné s hypergeometrickou distribúciou
-Úspechy čísel alebo víťazných kombinácií hazardných hier.
Môže vám slúžiť: Súbežné vektory: Charakteristiky, príklady a cvičenia-Výber určitého počtu žien alebo mužov vo vzorke n rýb z rýb z rýb.
Vyriešené cvičenia
Cvičenie 1
Štúdia zistila, že náhodne vybraných dospelých, ktorí majú smartfóny, ich 54% používa v triede alebo na stretnutiach. Chcete nájsť pravdepodobnosť, že náhodne vyberte 8 ľudí so smartfónom, presne 6 z nich ich používa v triede alebo na stretnutiach.
Riešenie
Tento experiment súhlasí s binomickým experimentom, pretože výsledok je binárny: osoba vezme telefón v triede alebo ho nevyberie. Skutočnosť, že osoba používa telefón v triede, sa dá nazvať úspech a zlyhanie, ak to neurobí (predtým, ako bolo vysvetlené, že táto voľba je úplne svojvoľná).
V takom prípade: p = 0.54 a Q = 1- 0.54 = 0.46.
Pretože 8 ľudí je náhodne vybraných, potom n = 8 a hodnota x je 6, preto sú k dispozícii potrebné hodnoty, ktoré ich nahradia vo vzorci binomického rozloženia:
Cvičenie 2
Za posledný rok klinika zaregistrovala 4221 narodení. S týmito jedinečnými údajmi určte pravdepodobnosť, že za 1 deň dôjde k 15 narodeniu. Je táto udalosť zriedkavá?
Riešenie
Používa sa Distribúcia Poissona, pretože sa vyžaduje, aby sa určila pravdepodobnosť výskytu udalosti, ktorá sa vyskytuje v časovom intervale. V tomto prípade je premenná množstvo pôrodov a interval je 1 deň.
Poissonov distribučný vzorec potrebuje priemerné narodenie za deň, ktorý sa ľahko vypočíta:
Preto je pravdepodobnosť x = 15 pôrodov/deň:
Výsledok je možné vyjadriť z hľadiska percentuálneho podielu pre prehľadnosť: 6.42% pravdepodobné, že v ktoromkoľvek dni sa vyskytne presne 15 narodení. Táto udalosť je nepravdepodobná, hoci v žiadnom prípade nemožné.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)