Normálne rozdelenie vzorcov, charakteristiky, príklad, cvičenie

Ten normálna distribúcia o Gaussovská distribúcia je rozdelenie pravdepodobnosti v kontinuálnej premennej, v ktorej je funkcia hustoty pravdepodobnosti opísaná exponenciálnou funkciou kvadratického a negatívneho argumentu, čo vedie k štiepanej forme.

Normálny názov distribúcie pochádza zo skutočnosti, že toto rozdelenie je taká, ktorá sa uplatňuje na najväčší počet situácií, keď je v danej skupine alebo populácii zapojená určitá nepretržitá náhodná premenná.

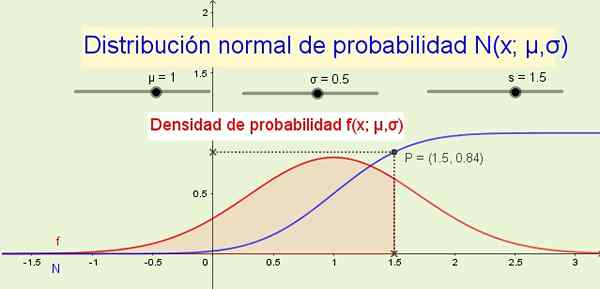
postava 1. Normálna distribúcia n (x; μ, σ) a jeho pravdepodobnosť hustota f (s; μ, σ). (Vlastné rozpracovanie)

Ako príklady, kde sa uplatňuje normálne rozdelenie: Výška mužov alebo žien, variácie v rozsahu fyzickej veľkosti alebo v merateľných psychologických alebo sociologických znakoch, ako je intelektuálny kvocient alebo spotrebné návyky určitého produktu.

Na druhej strane sa to nazýva gaussovská distribúcia alebo Gauss Bell, pretože je to tento nemecký matematický génius, ktorý sa pripisuje jeho objav za použitie na opis štatistickej chyby astronomických meraní už v roku 1800.

Tvrdí sa však, že túto štatistickú distribúciu predtým publikoval ďalší veľký matematik francúzskeho pôvodu, rovnako ako Abraham de Moivre, už v roku 1733.

[TOC]

Vzorec

Na normálnu distribučnú funkciu v kontinuálnej premennej X, S parametrami μ a σ Označuje to:

N (x; μ, σ)

A výslovne je napísané takto:

N (x; μ, σ) = ∫_-∞^X f (s; μ, σ) ds

kde f (u; μ, σ) Je to funkcia hustoty pravdepodobnosti:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s²/(2σ²)

Konštanta, ktorá vynásobí exponenciálnu funkciu vo funkcii hustoty pravdepodobnosti, sa nazýva normalizačná konštanta a bola vybraná takým spôsobom, že:

N (+∞, μ, σ) = 1

Predchádzajúci výraz zaisťuje, že pravdepodobnosť, že náhodná premenná X byť medzi -∞ a +∞ buď 1, to je 100% pravdepodobnosť.

Parameter μ Je to aritmetický priemer nepretržitej náhodnej premennej x a σ Štandardná odchýlka alebo druhá odmocnina rozptylu tej istej premennej. V takom prípade μ = 0 a σ = 1 Máte typické normálne štandardné alebo normálne rozdelenie distribúcie: 

N (x; μ = 0, σ = 1)

Normálne distribučné charakteristiky

1- Ak náhodná štatistická premenná sleduje distribúciu normálnej pravdepodobnosti hustoty f (s; μ, σ), Väčšina údajov je zoskupená okolo priemernej hodnoty μ A sú rozptýlené okolo nich, aby sa hneď za údajmi patria medzi dátami μ - σ a μ + σ. 

Môže vám slúžiť: Absolútna frekvencia: vzorec, výpočet, distribúcia, príklad

2- Štandardná odchýlka σ Je to vždy pozitívne.

3- Forma funkcie hustoty F Pripomína to zvonček, takže táto funkcia sa často nazýva Gaussov Bell alebo Gaussovská funkcia. 

4- v gaussovskej distribúcii sa priemerná, stredná a módna zhoduje.

5- Inflexné body funkcie hustoty pravdepodobnosti sa nachádzajú presne v μ - σ a μ + σ.

6- Funkcia F je symetrická vzhľadom na os, ktorá prechádza priemernou hodnotou μ A máte nulovú asymptoticky pre x ⟶ +∞ a x ⟶ -∞.

7- vyššia hodnota σ Väčšia disperzia, hluk alebo dištancované údaje okolo priemernej hodnoty. To znamená väčšie σ Tvar zvončeka je otvorenejší. Namiesto toho σ Small naznačuje, že kocky plávajúce do priemeru a tvar zvončeka sú uzavretejšie alebo špicaté.

8- Distribučná funkcia N (x; μ, σ) označuje pravdepodobnosť, že náhodná premenná je menšia alebo rovná sa X. Napríklad na obrázku 1 (vyššie) pravdepodobnosť p, že premenná X je menej alebo rovná 1.5 je 84% a zodpovedá oblasti pri funkcii hustoty pravdepodobnosti f (x; μ, σ) Od -∞ do X.

Intervaly dôvery

9- Ak údaje sledujú normálnu distribúciu, potom 68,26% z nich je medzi μ - σ a μ + σ.

10- 95,44% údajov, ktoré nasledujú po normálnom rozdelení, sú medzi μ - 2σ a μ + 2σ.

11- 99,74% údajov, ktoré nasledujú po normálnom rozdelení, sú medzi μ - 3σ a μ + 3σ.

12- Ak náhodná premenná X Postupujte podľa distribúcie N (x; μ, σ), Potom premenná

Z = (x - μ) / σ  Postupujte podľa štandardnej normálnej distribúcie  N (z; 0,1).

Zmena premennej X do z Nazýva sa štandardizácia alebo typizácia a je veľmi užitočná v čase použitia štandardných distribučných tabuliek na údaje, ktoré nasledujú po normálnom neštandardnom distribúcii.

Normálne distribučné aplikácie

Na použitie normálnej distribúcie je potrebné prejsť výpočtom integrálu hustoty pravdepodobnosti, ktorý z analytického hľadiska nie je ľahký a nie je vždy k dispozícii počítačový program, ktorý umožňuje jeho numerický výpočet. Na tento účel sa používajú štandardné alebo typické hodnoty, čo nie je nič iné ako normálne rozdelenie v prípade μ = 0 a σ = 1.

Môže vám slúžiť: kombinované operácie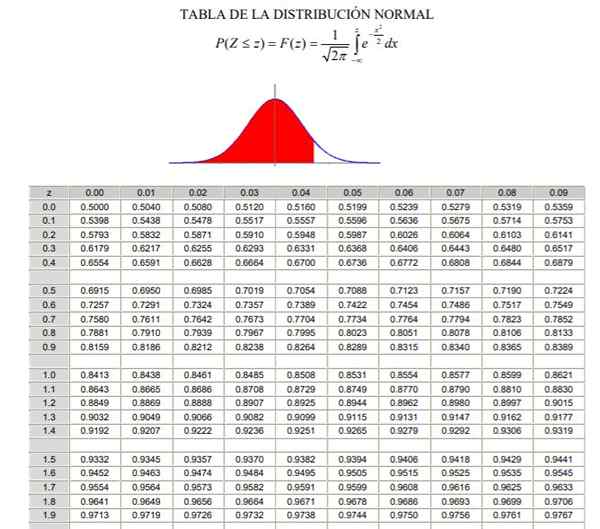Typifikovaná tabuľka normálnej distribúcie (časť 1/2) 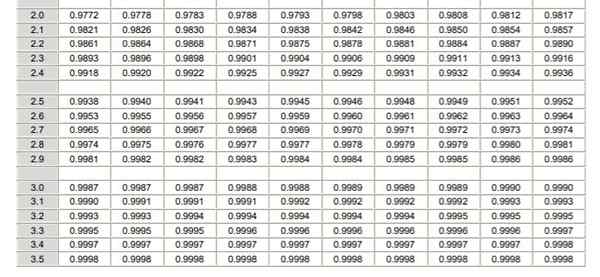Typifikovaná tabuľka normálnej distribúcie (časť 2/2)

Je potrebné poznamenať, že tieto tabuľky neobsahujú záporné hodnoty. Avšak pri použití vlastností symetrie funkcie hustoty pravdepodobnosti gaussov je možné získať zodpovedajúce hodnoty. V rozlíšenom cvičení uvedenom nižšie je v týchto prípadoch uvedené použitie tabuľky.

Príklad

Predpokladajme, že máte náhodný súbor údajov X, ktoré sledujú normálnu priemernú distribúciu 10 a štandardnú odchýlku 2. Žiada sa, aby sa našla pravdepodobnosť, že:

a) Náhodná premenná x je menšia alebo rovná 8.

b) je menší alebo rovný 10.

c) Táto premenná x je pod 12.

d) pravdepodobnosť, že hodnota x je medzi 8 a 12.

Riešenie:

a) Odpovedať na prvú otázku, ktorú musíte len vypočítať:

N (x; μ, σ)

S x = 8, μ = 10 a σ = 2. Uvedomujeme si, že je to integrál, ktorý nemá analytické riešenie v elementárnych funkciách, ale riešenie je vyjadrené podľa funkcie chyby Erf (x).

Na druhej strane existuje možnosť vyriešiť integrál numerickým spôsobom, čo je to, čo mnohí kalkulačky, tabuľky a počítačové programy, ako napríklad Geogebra do. Nasledujúci obrázok zobrazuje numerické riešenie zodpovedajúce prvému prípadu:

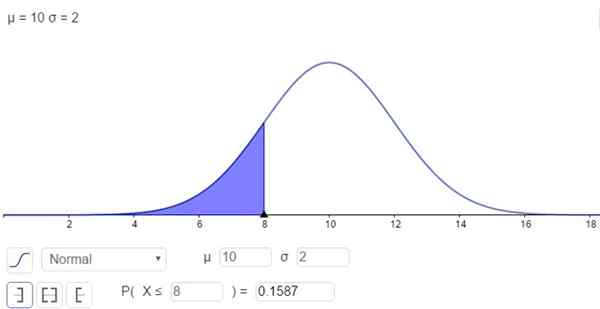Obrázok 2. Hustota pravdepodobnosti F (x; μ, σ). Zatienená plocha predstavuje p (x ≤ 8). (Vlastné rozpracovanie)

Odpoveď je, že pravdepodobnosť, že X je pod 8, je:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0,1587

b) V tomto prípade ide o nájdenie pravdepodobnosti, že náhodná premenná x je pod priemerom, že v tomto prípade má hodnotu 10. Odpoveď nevyžaduje žiadny výpočet, pretože vieme, že polovica údajov je pod priemerom a druhou polovicou nad priemerom. Odpoveď je preto:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) Odpovedať na túto otázku, musíte vypočítať N (x = 12; μ = 10, σ = 2), čo sa dá urobiť pomocou kalkulačky, ktorá má štatistické funkcie alebo softvérom, ako je Geogebra:

Môže vám slúžiť: DETIVORY 8: Čo sú a ľahké vysvetlenie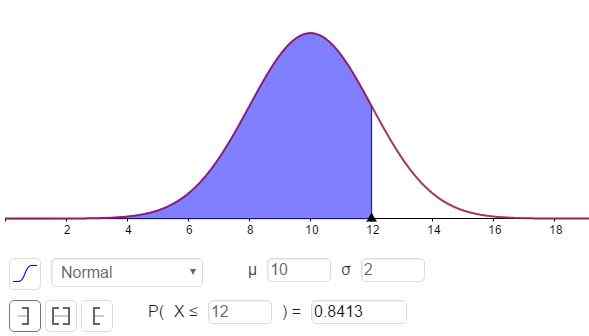Obrázok 3. Hustota pravdepodobnosti F (x; μ, σ). Tieňovaná plocha predstavuje p (x ≤ 12). (Vlastné rozpracovanie)

Odpoveď na časť C je možné vidieť na obrázku 3 a je:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

d) Na nájdenie pravdepodobnosti, že náhodná premenná X je medzi 8 a 12, môžeme použiť výsledky častí A a C nasledovne:

P (8 ≤ x ≤ 12) = P (x ≤ 12) - P (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Cvičenie

Priemerná cena akcií spoločnosti je 25 dolárov so štandardnou odchýlkou ​​4 USD. Určiť pravdepodobnosť, že:

a) Akcia má cenu menej ako 20 dolárov.

b) To má cenu vyššiu ako 30 dolárov.

c) Cena je medzi 20 a 30 dolárov.

Na nájdenie odpovedí použite tabuľky normálnych distribúcií.

Riešenie:

Na použitie tabuliek je potrebné presunúť sa na normalizovanú alebo typovanú premennú:

20 dolárov v štandardizovaných premenných rovnocenných z = (20 dolárov - 25 dolárov) / $ 4 = -5/4 = -1,25 a 

30 dolárov v štandardizovaných premenných rovnocenných Z = (30 dolárov - 25 dolárov) / $ 4 = +5/4 = +1,25.

a) 20 dolárov je rovnocenná s -1,25 v štandardizovanej premennej, ale tabuľka nemá žiadne záporné hodnoty, takže umiestnime hodnotu +1,25, ktorá zobrazuje hodnotu 0,8944.

Ak sa táto hodnota odpočíta 0,5, výsledkom bude oblasť medzi 0 a 1,25, ktorá je mimochodom rovnaká (symetriou) s oblasťou medzi -1.25 a 0. Výsledok odčítania je 0,8944 - 0,5 = 0,3944, čo je oblasť medzi -1.25 a 0.

Ale záujmy oblasti od -∞ do -1,25, ktoré budú 0,5 -0,3944 = 0,1056. Preto sa dospelo k záveru, že pravdepodobnosť, že akcia je pod 20 dolárov, je 10,56%.

b) 30 dolárov v typickej premennej z je 1,25. Pre túto hodnotu v tabuľke sa objaví číslo 0,8944, ktoré zodpovedá oblasti od -∞ do +1,25. Oblasť medzi +1.25 y +∞ je (1 - 0,8944) = 0,1056. Inými slovami, pravdepodobnosť, že akcia stojí viac ako 30 dolárov, je 10,56%.

c) Pravdepodobnosť, že akcia má náklady medzi 20 a 30 dolárov, sa vypočíta takto:

100% -10,56% - 10,56% = 78,88%

Odkazy

1. Štatistika. Normálna distribúcia. Zdroj: ProjectodesCartes.orgán
2. Geogebra. Classic Geogebra, výpočet pravdepodobnosti. Zotavené z geogebra.orgán
3. Matematika. Distribúcia. Obnovené z: je.Matematika.com
4. Mendenhall, W. 1981. Štatistiky pre správu a ekonomiku. Tretí. vydanie. Redakčná skupina Iberoamerica.
5. Trek. Naučte sa štatistiky. Poisson Distribúcia. Obnovené z: stattrek.com,
6. Triola, m. 2012. Štatistika. 11. Edimatizovať. Pearson Vzdelanie.
7. University of Vigo. Hlavné nepretržité rozdelenie. Získané z: Anapg.webové stránky.Uvigo.je
8. Wikipedia. Normálna distribúcia. Obnovené z: je.Wikipedia.orgán