Všeobecná kultúra a spoločnosť

Exponenciálne rozdelenie

4601
367
Denis Škriniar

Vysvetľujeme, čo je exponenciálne rozdelenie, jeho charakteristiky, vzorce, príklady a vyriešené cvičenia

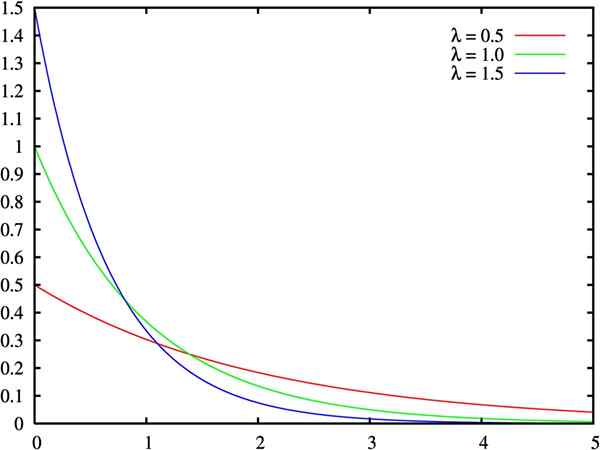
Graf funkcie hustoty exponenciálneho rozdelenia pre tri hodnoty parametra Lambda. Zdroj: Wikimedia Commons.

Čo je exponenciálne rozdelenie?

Ten exponenciálne rozdelenie Je to pravdepodobnostný model pre nepretržité náhodné premenné. To znamená, že prostredníctvom neho môžete poznať pravdepodobnosť výskytu určitej hodnoty premennej, takže ide o rozdelenie pravdepodobnosti.

Na získanie distribúcie začína z a funkcia hustoty, ktorý má exponenciálny tvar parametra λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ text Jo x \ leq 0 \ End prípady$

Funkcia hustoty ako taká neumožňuje výpočet pravdepodobnosti, ale akonáhle sa stanoví F (x), distribučná funkcia f (x), pomocou ktorej sa pravdepodobnosti získajú, sa získa integráciou F (x). Napríklad pravdepodobnosť p, že náhodná premenná má hodnoty medzi 0 a x, je:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Vykonanie integrácie, ktorá je veľmi jednoduchá, pretože integrál exponenciálu je rovnaký exponenciál, s výnimkou konštantných látok, ktoré sprevádzajú argument, získa sa:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

Exponenciálne rozdelenie sa široko používa na určenie pravdepodobnosti udalosti po určitej čakacej dobe, napríklad čas, ktorý sa odohráva pri výskyte nemocnice pred príchodom pacienta.

Udalosti sa často vzťahujú na zlyhanie alebo rozpad elektrických, elektronických a iných typov. V tomto prípade exponenciálne rozdelenie pomáha odhadnúť čas potrebný na zlyhanie komponentu, a tiež čas medzi opravami. Toto je známe ako teória spoľahlivosti.

Charakteristiky exponenciálneho rozdelenia

Niektoré z najvýznamnejších vlastností funkcie hustoty F (x) exponenciálneho rozdelenia sú nasledujúce:

f (x) je pozitívny.
Plocha pod krivkou y = f (x) = λe^−λ^X Vždy sa rovná 1, pretože súčet pravdepodobností výskytu všetkých hodnôt premennej musí byť 1. Toto je podmienka, ktorá funguje hustota. Táto oblasť sa počíta prostredníctvom integrálu:

Môže vám slúžiť: Anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Nedostatok exponenciálnej distribučnej pamäte

Najvýznamnejšou črtou exponenciálnej distribúcie je nedostatok pamäte. Napríklad predpokladajme, že uplynutý čas sa modeluje s týmto rozdelením, až kým nedôjde k zlyhaniu prvku.

Nedostatok pamäte sa vzťahuje na to, že prvok fungoval pre čas prežitia „S“, nemenuje pravdepodobnosť, že prvok bude naďalej bežať až do určitého dodatočného času „T“.

To znamená, že pravdepodobnosť, že prvok zlyhá odtiaľ do určitého času (napríklad 1 minúta, 1 hodinu), nezávisí od toho, že doteraz dobre fungoval.

Matematicky sa vypočíta podľa definície pravdepodobnosti nezávislých udalostí:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Preto pravdepodobnosť nezávisí od času S alebo prežitia.

Vzorce

1.- Funkcia hustoty exponenciálneho rozdelenia je:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ text Jo x \ leq 0 \ End prípady$

Kde λ je distribučný parameter.

2.- Ako je uvedené vyššie, samotné rozdelenie pravdepodobností sa označuje ako F (x) a rôzne pravdepodobnosti sa získavajú integráciou funkcie hustoty:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ End prípady$

3.- Z vyššie uvedeného vyplýva, že pravdepodobnosť, že premenná berie hodnoty menšie alebo rovnajúce sa „x“, je p [x −λ^X.

4.- Plocha pod krivkou y = f (x), zahrnutá medzi A a B, umožňuje vypočítať pravdepodobnosť, že premenná je v intervale [a, b]. Táto oblasť je:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- Hodnota p [x ≥ a] je 1 - f (a) = 1 - (1 - e^−λ^X) = e^−λ^X

Očakávaná hodnota exponenciálneho rozdelenia

Nádej alebo očakávaná hodnota E (x) exponenciálneho rozdelenia je hodnota, ktorá sa očakáva častejšie. Vypočíta sa z integrálu:

Môže vám slúžiť: techniky registrácie informácií

$E(x)=\int_0^\infty xf(x)dx$ Ktorý je ľahko vyriešený metódou integrácie podľa častí. Výsledkom je:

E (x) = 1/λ

Rozptyl exponenciálnej distribúcie

Na výpočet rozptylu je potrebné určiť integrál:

$Var(x)=\int_0^\infty x^2f(x)dx$

Ktorá je tiež vyriešená metódou integrácie podľa častí, aby sa získalo:

Var (x) = 1/λ²

Osobitnosťou exponenciálneho rozdelenia je to, že štandardná odchýlka S (x), definovaná ako druhá odmocnina rozptylu je:

S (x) = √var (x) = √ (1/λ²) = 1/λ

To znamená, že štandardná odchýlka sa rovná nádeji na distribúciu.

Príklady exponenciálneho rozdelenia

Datation vzoriek uhlíka 14

Exponenciálne rozdelenie sa používa na určenie času potrebného na rozpad rádioaktívnej častice. Tieto časy sa doteraz používajú fosílne vzorky pomocou rádioaktívneho uhlia.

Čas na kontrolu pošty

Môžete modelovať čas, ktorý používatelia berú na kontrolu svojho e -mailu, po prijatí oznámenia prostredníctvom exponenciálnej distribúcie. Predpokladajme, že distribučný parameter je λ = 0.2, pravdepodobnosť, že osoba trvá menej ako 1 minútu, aby skontrolovala jeho e -mail:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Tento integrál bol vyriešený na začiatku, zostáva iba nahradením číselných hodnôt v riešení a vypočítať konečný výsledok:

P [x ≤ 1] = 1 --e^-^0.2^×¹ = 1- e^-^0.2 = 1- 0.819 = 0.181

Môže sa tiež priamo vymeniť za funkciu F (x) uvedenú vyššie, aby sa získal f (1).

Cvičenia

Cvičenie 1

Nájdite pravdepodobnosť, že osoba neskôr jednu hodinu preskúma svoj e -mail, ak je rozdelenie pravdepodobnosti exponenciálne, s parametrom λ = 0.2.

Riešenie

P [x ≥ 60] sa musí vypočítať, pretože 1 hodina je rovnocenná 60 minútami a pravdepodobnosť, že osoba neskoro 60 minút alebo viac na kontrolu pošty. Pravdepodobnosť sa vypočíta s rovnakým integrálom uvedeným na začiatku, iba zmenou limitov integrácie:

Môže vám slúžiť: rapa nui: História, vlastnosti, kultúra, tradície

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

Získaná hodnota je malá, takže je veľmi nepravdepodobné, že by osoba trvala viac ako hodinu na kontrolu svojho e -mailu.

Cvičenie 2

Elektrické žiarovky majú zvyčajne konečné trvanie, s výnimkou slávnej žiarovky hasičskej stanice v Livermore v Kalifornii, ktorá od tej doby nikdy zlyhala v roku 1901, v roku 1901.

Predpokladajme, že trvanie súčasnej žiarovky sleduje exponenciálne rozdelenie s očakávanou hodnotou 8 mesiacov. Vypočítať:

a) Aká je pravdepodobnosť, že žiarovka bude trvať od 5 do 14 mesiacov?

b) Pravdepodobnosť, že žiarovka bude trvať viac ako 25 mesiacov, s vedomím, že má v prevádzke viac ako 11 mesiacov.

Roztok

Prvá vec je nájsť hodnotu λ prostredníctvom očakávanej hodnoty distribúcie E (x) = 8 mesiacov. Podľa toho, čo bolo povedané v predchádzajúcej časti, je očakávaná hodnota inverzia parametra λ, preto:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Potom sa vypočíta požadovaná pravdepodobnosť prostredníctvom integrálu uvedeného na začiatku, ale pohodlne zmenou limitov integrácie:

Potom sa nahradí vo funkcii F (x) uvedenej v predchádzajúcej časti:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Riešenie B

Na zodpovedanie tohto problému sa použije vlastnosť nedostatku pamäte, uvedená vyššie. Ako je známe, že už trvalo viac ako 11 mesiacov, potom:

S = 11 mesiacov

Dodatočný čas na trvanie 25 mesiacov alebo viac je:

T = 14 mesiacov

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{−0.125 × 14}= 0.174