Euclidovský koncept vzdialenosti, vzorec, výpočet, príklad

Ten Euklidovská vzdialenosť Je to pozitívne číslo, ktoré naznačuje oddelenie, ktoré majú dva body v priestore, kde sú splnené axiómy a vety euklidovej geometrie.

Vzdialenosť medzi dvoma bodmi A a B euklidovského priestoru je dĺžka vektora AB Patriaci k jedinému riadku, ktorý prechádza týmito bodmi.

postava 1 . Jednorozmerný euklidovský priestor tvorený čiarom (OX). Niekoľko bodov v tomto priestore, sú zobrazené ich súradnice a vzdialenosti. (Pripravil Ricardo Pérez).

Priestor, ktorý vnímame a kde pohybujeme ľudskými bytosťami, je trojrozmerný priestor (3-D), kde sú splnené axiómy a vety euklidovej geometrie. V tomto priestore sú dvojrozmerné podpriestory (plány) a jednotlivé (rovné) (priame) podprostory.

Euklidovské priestory môžu byť z jednej dimenzie (1-D), dvojrozmerných (2-D), troch rozmerov (3-D) alebo N rozmerov (N-d).

Toto sú body v jednom -rozmernom priestore X, ktoré patria do orientovanej čiary (OX), smer z alebo do x je kladná adresa. Na nájdenie bodov na tomto riadku sa používa karteziánsky systém, ktorý pozostáva z priradenia každého bodu riadku.

[TOC]

Vzorec

Euklidovská vzdialenosť D (A, B) je definovaná medzi bodmi A a B, umiestnenými na čiare, ako je druhá štvorcová koreň štvorca rozdielov jeho súradníc X:

D (a, b) = √ ((xb - xa)^2)

Táto definícia zaručuje, že: vzdialenosť medzi dvoma bodmi je vždy pozitívna suma. A že vzdialenosť medzi A a B sa rovná vzdialenosti medzi B a a.

Obrázok 1 zobrazuje jedno -rozmerový euklidovský priestor vytvorený čiarom (OX) a niekoľko bodov na tejto čiare. Každý bod má súradnicu:

Bod A má xa súradnicu = 2.5, súradnica B xB = 4 a súradnica bodu C xc = -2.5

Môže vám slúžiť: Pravdepodobnosť frekvencie: koncept, ako sa vypočíta a príklady

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Euklidovská vzdialenosť v dvoch rozmeroch

Dvojrozmerný euklidový priestor je lietadlo. Body euklidovskej roviny spĺňajú napríklad axiómy euklidovej geometrie:

- Na dvoch bodoch prechádza jeden riadok. 

- Tri body v rovine tvoria trojuholník, ktorého vnútorné uhly vždy pridávajú 180 °.

- V obdĺžnikovom trojuholníku sa štvorec hypotenusu rovná súčtu štvorcov jeho nôh.

V dvoch rozmeroch má bod X a Y súradnice. 

Napríklad bod P má súradnice (XP, YP) ​​a bod, ktorý koordinuje (XQ, YQ).

Euklidovská vzdialenosť medzi bodom P a Q je definovaná s nasledujúcim vzorcom:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Je potrebné poznamenať, že tento vzorec je ekvivalentný s Pythagorovou vetou, ako je znázornené na obrázku 2.

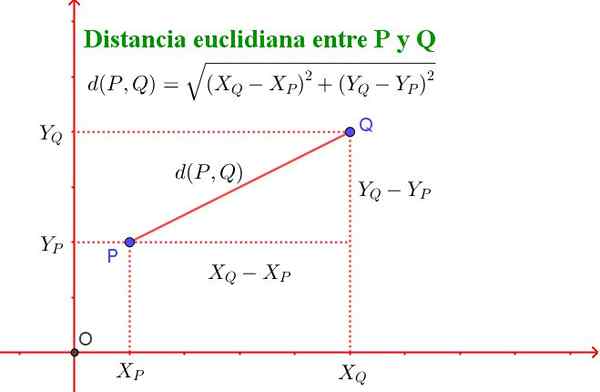Obrázok 2. Vzdialenosť medzi dvoma bodmi P a Q lietadla sa stretáva s vetou Pythagoras. (Pripravil Ricardo Pérez).

Nonuklidské povrchy

Nie všetky dva rozmerové priestory spĺňajú euklidovskú geometriu. Povrch gule je dvojrozmerný priestor.

Uhly trojuholníka na sférickom povrchu nepridajú 180 ° a vďaka tomu nie je splnená veta Pythagoras, preto sférický povrch nespĺňa axiómy euklid.

Euklidovská vzdialenosť v N rozmeroch

Koncept súradníc možno rozšíriť na väčšie rozmery:

- V 2-D bodu P má súradnice (XP, YP)

- V 3-D bod, ktorý má súradnice (XQ, YQ, ZQ)

- V 4-D bodu R bude mať súradnice (XR, YR, ZR, WR)

- V n-d A bod P bude mať súradnice (p1, p2, p3, ..., pn)

Môže vám slúžiť: Bars Graf: Charakteristiky, na čo je to, príklady

Vzdialenosť medzi dvoma bodmi P a Q v dimenzionálnom euklidovskom priestore sa vypočíta s nasledujúcim vzorcom:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +… +(qn - pn)^2)

Geometrické miesto všetkých bodov, ktoré v N-dimenzionálnom euklidovskom priestore, ktoré sa rovnajú inému pevnému bodu P (stred) tvoria N-dimenzionálnu hypersfera.

Ako vypočítať euklidovskú vzdialenosť

Nižšie sa vypočíta vzdialenosť medzi dvoma bodmi umiestnenými v euklidovskom trojrozmernom priestore.

Predpokladajme bod A karteziánskych súradníc x, y, z daný A :( 2, 3, 1) a bod B súradníc B :( -3, 2, 2).

Chcete určiť vzdialenosť medzi týmito bodmi, pre ktoré sa používa všeobecný vzťah:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 )

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5,196

Príklad

Existujú dva body p a q.  Bod P pre karteziánske súradnice x, y, z daný p :( 2, 3, 1) a bod Q súradníc Q :( -3, 2, 1).

Žiada sa, aby našla súradnice stredného bodu M segmentu [pq], ktorý spája tieto dva body. 

Riešenie:

Predpokladá sa, že neznámy bod M má súradnice (x, y, z).

Pretože m je priemerný bod [pq], musí sa splniť, že d (p, m) = d (q, m), takže sa musí splniť aj d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Rovnako ako v tomto prípade je tretie funkčné obdobie rovnaké v oboch členoch, predchádzajúci výraz je zjednodušený:

Môže vám slúžiť: Absolútna konštanta

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Potom existuje rovnica s dvoma neznámymi x a y. Na vyriešenie problému je potrebná ďalšia rovnica.

Bod M patrí do čiary, ktorá prechádza cez body P a Q, ktoré môžeme vypočítať nasledovne:

Prvým je vektor režiséra Pq riadku: Pq = = = .

Potom POPOLUDNIE = Oproti + do Pq, kde Oproti Je to vektorová poloha bodu P a do Je to parameter, ktorý patrí do skutočných čísel. 

Predchádzajúca rovnica je známa ako vektorová rovnica línie, ktorá v karteziánskych súradniciach prijíma nasledovne:

= + a =

Rovnaké zodpovedajúce komponenty sú:

X - 2 = 2 - 5 a; A - 3 = 3 -a; Z - 1 = 0

To znamená, že x = 4 - 5a, y = 6 - a, nakoniec z = 1.

Nahradí sa v kvadratickom výraze, ktorý sa týka x s y:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

Je to zjednodušený:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Teraz sa vyvíja:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Zjednodušila sa a zrušila podobné podmienky u oboch členov:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parameter A:

52 A = 49 + 16 - 4 - 9 = 52, čo vedie k tomu, že a = 1.

To znamená, že x = 4 - 5, y = 6 - 1, nakoniec z = 1.

Nakoniec získame karteziánske súradnice stredu m segmentu [PQ]:

M: (-1, 5, 1).

Odkazy

1. Lehmann C. (1972) Analytická geometria. Uteha.
2. Superprof. Vzdialenosť medzi dvoma bodmi. Obnovené z: Superprof.je
3. Žobrák. Vzdialenosť medzi príbuznými sublinickými odrodami. Získané z: Prometheus.Matem.Žobrák.mx/
4. Wikipedia. Euklidovská vzdialenosť. Obnovené z: je.Wikipedia.com
5. Wikipedia. Euklidovský priestor. Obnovené z: je.Wikipedia.com