Vzorec rozširovania povrchu, koeficienty a príklady

Ten povrchná dilatácia Je to expanzia, ktorá sa vyskytuje, keď objekt pociťuje variácie jeho povrchu v dôsledku zmeny teploty. Je to kvôli charakteristikám materiálu alebo jeho geometrického tvaru. Dilatácia prevláda v dvoch rozmeroch v rovnakom pomere.

Napríklad v hárku, keď existuje variácia teploty, je to rovnaký povrch, ktorý trpí najväčšou zmenou v dôsledku tepelnej dilatácie.

Povrch kovovej dosky, ktorá sa zvyčajne vyskytuje na uliciach. Zdroj: Pixabay.

Kovový list predchádzajúceho obrázku zvyšuje svoju širokú a jej dĺžku, keď sa zahrieva slnečným žiarením. Naopak, obe sa pri ochladení výrazne znížia z dôvodu zníženia teploty okolia.

Z tohto dôvodu, že keď sú dlaždice inštalované na jednom poschodí, nemali by byť zasiahnuté niektoré hrany s ostatnými, ale musí existovať oddeľovací priestor nazývaný dilatačná doska.

Okrem toho je tento priestor vyplňovaný špeciálnou zmesou, ktorá má určitý stupeň flexibility, ktorá bráni praskaniu dlaždíc v dôsledku silných tlakov, ktoré môže tepelná dilatácia produkovať.

[TOC]

Čo je povrchová dilatácia?

V pevnom materiáli si atómy udržiavajú viac alebo menej pevné relatívne polohy okolo rovnovážneho bodu. Avšak z dôvodu tepelného agitácie sa okolo neho vždy oscilujú.

Zvýšením teploty sa tiež zvyšuje tepelná oscilácia, čo spôsobuje zmenu pozícií strednej oscilácie. Je to preto, že potenciál spojenia nie je presne parabolický a má asymetriu okolo minima.

Nižšie je obrázok, ktorý načrtáva energiu chemickej väzby v závislosti od interatomickej vzdialenosti. Je tiež znázornená celková oscilačná energia pri dvoch teplotách a ako sa pohybuje oscilačné centrum.

Môže vám slúžiť: Pascal Tonel: Ako to funguje a experimentuje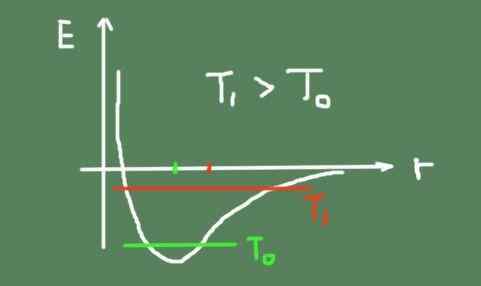Spojte energetický graf verzus interatomická vzdialenosť. Zdroj: Self Made.

Povrchová dilatácia a jej koeficient

Na meranie povrchovej dilatácie začíname z počiatočnej oblasti A a počiatočnej teploty t, ktorého objekt sa má merať.

Predpokladajme, že tento objekt je lamina oblasti A, a jeho hrúbka je oveľa nižšia ako druhá druhá koreň oblasti a. List je vystavený variácii teploty AT, takže konečná teplota rovnakej teploty, keď bude stanovená tepelná rovnováha so zdrojom tepla, bude T '= T+ AT.

Počas tohto tepelného procesu sa povrchová plocha zmení aj na novú hodnotu pri '= a + δa. Koeficient dilatácie povrchu σ je teda definovaný ako pomer medzi relatívnou zmenou plochy na jednotku variácie teploty.

Nasledujúci vzorec definuje povrchový koeficient dilatácie σ:

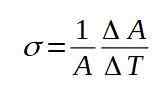
Koeficient povrchového dilatácie σ je prakticky konštantný pre široký rozsah hodnôt teploty.

Kvôli definícii σ je jeho rozmery inverzná teplota. Ako jednotka sa zvyčajne používa ° C^-1.

Koeficient povrchovej dilatácie pre rôzne materiály

Ďalej uvádzame zoznam povrchových dilatačných koeficientov pre niektoré materiály a prvky. Koeficient sa vypočíta v normálnom atmosférickom tlaku na základe okolitej teploty 25 ° C a jeho hodnota sa považuje za konštantnú v rozsahu AT od -10 ° C do 100 ° C.

Jednotka povrchového dilatačného koeficientu bude (° C)^-1

- Oceľ: σ = 24 ∙ 10^-6 (° C)^-1

- Hliník: σ = 46 ∙ 10^-6 (° C)^-1

Môže vám slúžiť: magnetizácia: orbitálny a rotátny magnetický moment, príklady

- Zlato: σ = 28 ∙ 10^-6 (° C)^-1

- Meď: σ = 34 ∙ 10^-6 (° C)^-1

- Mosadz: σ = 36 ∙ 10^-6 (° C)^-1

- Železo: σ = 24 ∙ 10^-6 (° C)^-1

- Sklo: σ = (14 až 18) ∙ 10^-6 (° C)^-1

- Kremeň: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamant: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Olovo: σ = 60 ∙ 10^-6 (° C)^-1

- Dubové drevo: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Uhlíkové vlákno: σ = -1,6 ∙ 10^-6 (° C)^-1

- Betón: σ = (16 až 24) ∙ 10^-6 (° C)^-1

Väčšina materiálov sa tiahne so zvýšením teploty. Niektoré materiály, ako napríklad uhlíkové vlákna, však spĺňajú zvýšenie teploty.

Vyriešené príklady povrchovej dilatácie

Príklad 1

Oceľová doska má rozmery 3 m x 5 m. Ráno av tieni je jeho teplota 14 ° C, ale v poludnie ho slnko zahreje až na 52 ° C. Nájdite konečnú plochu taniera.

Riešenie

Začneme z definície koeficientu povrchového dilatácie:

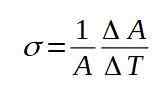
Odtiaľ vymažeme variácie v oblasti:

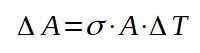
Potom pokračujeme v nahradení príslušných hodnôt, aby sme našli zvýšenie plochy so zvýšením teploty.

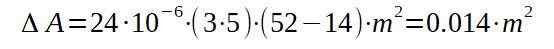
To znamená, že konečná oblasť bude 15 014 metrov štvorcových.

Príklad 2

Ukazujú, že koeficient povrchovej dilatácie je približne dvojnásobný koeficient lineárnej dilatácie.

Riešenie

Predpokladajme, že začíname z obdĺžnikovej doštičky rozmerov šírky lx a dlhé, potom jej počiatočná plocha bude a = lx ∙ ly ly

Môže vám slúžiť: teplometrické stupnice

Keď doska trpí zvýšením teploty AT, potom sa jej rozmery zvýši aj jej nová šírka LX 'a jej nový LY' Long, takže jej nová oblasť bude '= lx' ∙ ly '

Variácia, ktorú utrpí plocha dosky v dôsledku zmeny teploty

Δa = lx '∙ ly' - lx ∙ ly

kde lx '= lx (1 + a Δt) a ly' = ly (1 + a Δt)

To znamená, že zmena plochy v závislosti od koeficientu lineárneho dilatácie a zmeny teploty bude:

ΔA = lx (1 + a Δt) ∙ ly (1 + a Δt) - lx ∙ ly ly

Toto je možné prepísať ako:

ΔA = lx ∙ ly ∙ (1 + a Δt) ² - lx ∙ ly ly

Rozvoj štvorca a znásobenie máme nasledujúce:

I

Ako a je rádovo 10^-6, Zdvihnutím štvorca je to poradie 10^-12. Kvadratický termín v predchádzajúcom výraze je teda opovrhnutiahodné.

Potom sa k zvýšeniu oblasti dá osloviť:

Δa ≈ 2a Δt lx ∙ ly ly

Ale zvýšenie oblasti v závislosti od koeficientu povrchového dilatácie je:

ΔA = y Δt a

Odkedy je odvodený výraz, ktorý sa týka koeficientu lineárneho dilatácie s koeficientom povrchovej dilatácie.

γ ≈ 2 ∙ α

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. Mac Graw Hill. 422-527
2. Giancoli, D. 2006. Fyzika: Princípy s aplikáciami. 6. Vydanie. Sála. 238-249.