Nerovnosť demonštračného trojuholníka, príklady, cvičenia vyriešené

To sa nazýva Nerovnosť trojuholníka Na vlastníctvo, ktoré spĺňajú dve reálne čísla pozostávajúce z absolútnej hodnoty jeho súčtu, je vždy menšia alebo rovná súčtu jeho absolútnych hodnôt. Táto vlastnosť je známa aj ako Minkowski nerovnosť alebo trojuholníková nerovnosť.

Táto vlastnosť čísel sa nazýva trojuholníková nerovnosť, pretože v trojuholníkoch sa stáva, že dĺžka jednej strany je vždy menšia alebo rovná súčtu druhých dvoch, aj keď sa táto nerovnosť vždy uplatňuje v oblasti trojuholníkov.

postava 1. Absolútna hodnota súčtu dvoch čísel je vždy menšia alebo rovná súčtu jeho absolútnych hodnôt. (Pripravený r. Pérez)

Existuje niekoľko demonštrácií trojuholníkovej nerovnosti v reálnych číslach, ale v tomto prípade si vyberieme A na základe vlastností absolútnej hodnoty a štvorcového binomialu.

Veta: Pre všetky čísla do a b Patrí k skutočným číslam, musí:

| A + B | ≤ | a | + | B |

[TOC]

Demonštrácia

Začneme zvážením prvého člena nerovnosti, ktorý bude obmedzený:

| A + b |^2 = (a + b)^2 = a^2 + 2 a b + b^2 (ec. 1)

V predchádzajúcom kroku sa použila vlastnosť, že akékoľvek vysoké číslo na štvorcovi sa rovná absolútnej hodnote uvedeného čísla vysokého štvorca, to znamená: | x |^2 = x^2. Použil sa aj vývoj Square Binomial.

Všetky čísla X Je menej alebo rovná svojej absolútnej hodnote. Ak je číslo pozitívne, stojí za rovnosť, ale ak je číslo negatívne, bude vždy menšie ako kladné číslo. V tomto prípade jeho vlastná absolútna hodnota, to znamená, že sa dá povedať x ≤ | X |.

Môže vám slúžiť: nelineárne programovanie: metódy a cvičenia

Produkt (a b) Je to číslo, preto sa uplatňuje (že (a b) ≤ | A B |. Ak sa táto vlastnosť uplatňuje (EC. 1) Máme:

| A + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | A B | + B^2 (EC. 2)

Berúc do úvahy | A B | = | A || B | LA (EC. 2) Môže byť napísaný takto:

 | A + B |^2 ≤ A^2 + 2 | A || B | + B^2 (EC. 3)

Ako sme však už povedali, že štvorec čísla sa rovná absolútnej hodnote čísla vysokého štvorca, potom je možné rovnicu 3 prepísať takto:

 | A + b |^2 ≤ | a |^2 + 2 | a | | b | + | B |^2 (EC. 4)

U druhého člena nerovnosti sa uznáva pozoruhodný produkt, ktorý pri použití vedie k:

 | A + b |^2 ≤ (| a | + | b |)^2 (ec. 5)

V predchádzajúcom výraze by sa malo poznamenať, že hodnoty, ktoré sa majú zvýšiť pre oboch členov nerovnosti, sú tiež pozitívne, že je potrebné splniť aj to:

 | A + B | ≤ (| a |+ | b |) (EC. 6)

Predchádzajúci výraz je presne to, čo ste chceli demonštrovať.

Príklady

Ďalej skontrolujeme trojuholníkovú nerovnosť s niekoľkými príkladmi.

Príklad 1

Hodnota sa odoberie a = 2 a hodnota b = 5, to znamená obidva kladné čísla a overujeme, či je nerovnosť splnená alebo nie.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Rovnosť sa overuje, preto bola splnená veta nerovnosti trojuholníka.

Príklad 2

Nasledujúce hodnoty sú vybrané a = 2 a b = -5, to znamená kladné číslo a druhé negatívne, skontrolujeme, či je nerovnosť splnená alebo nie.

Môže vám slúžiť: trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Nerovnosť je splnená, preto bola overená trojuholníková nerovnosť.

Príklad 3

Hodnota sa odoberie a = -2 a hodnota b = 5, to znamená záporné číslo a ďalšie pozitívne, overujeme, či je nerovnosť splnená alebo nie.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Nerovnosť je overená, preto bola splnená veta.

Príklad 4

Vyberajú sa nasledujúce hodnoty a = -2 a b = -5.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Rovnosť sa overuje, preto bola splnená veta nerovnosti Minkowska.

Príklad 5

Hodnota sa odoberie a = 0 a hodnota b = 5, to znamená nulové číslo a druhé kladné, potom skontrolujeme, či je nerovnosť splnená alebo nie.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Rovnosť je splnená, preto bola overená veta nerovnosti trojuholníka.

Príklad 6

Hodnota sa odoberie a = 0 a hodnota b = -7, to znamená nulové číslo a druhé kladné, potom skontrolujeme, či je nerovnosť splnená alebo nie.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Rovnosť sa overuje, preto bola splnená trojuholníková nerovnosť.

Vyriešené cvičenia

V nasledujúcich cvičeniach geometricky predstavuje nerovnosť trojuholníka alebo nerovnosť Minkowski pre čísla A a B.

Môže vám slúžiť: Papomudas

Číslo A bude znázornené ako segment na osi x, jeho pôvod alebo sa zhoduje s nulou osi x a druhý koniec segmentu (v bode P) bude v kladnom smere (vpravo) x os, ak a> 0, ale do < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Podobne bude číslo B reprezentované ako segment, ktorého pôvod je v bode P. Druhý koniec, to znamená, bod, ktorý bude vpravo od P, ak B je pozitívny (b> 0) a bod Q bude | b | jednotky vľavo od P, ak b<0.

Cvičenie 1

Graficky predstavuje nerovnosť trojuholníka pre a = 5 a b = 3 | A + B | ≤ | a | + | B |, bytosť C = a + b. 

Riešenie 1: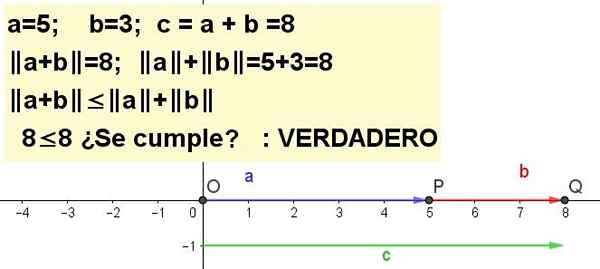

Cvičenie 2

Vytvorte graf trojuholníkovej nerovnosti pre a = 5 a b = -3. 

| A + B | ≤ | a | + | B |, bytosť C = a + b.

Riešenie 2:

Cvičenie 3

Graf nerovnosti trojuholníka pre a = -5 a b = 3.

| A + B | ≤ | a | + | B |, bytosť C = a + b. 

Riešenie 3: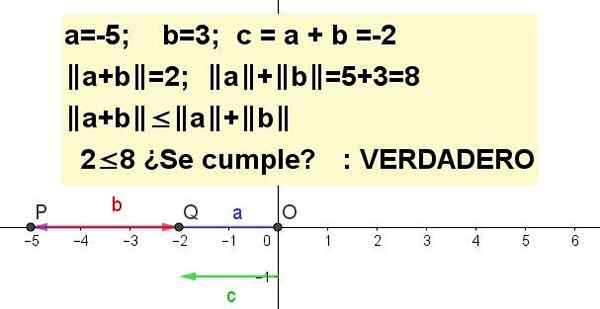

Cvičenie 4

Graf trojuholníkovej nerovnosti pre a = -5 a b = -3.

| A + B | ≤ | a | + | B |, bytosť C = a + b.

Riešenie 4: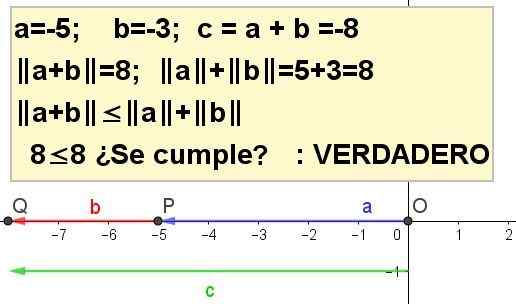

Odkazy

1. A. Biely. (1980).Booleovská algebra a jej aplikácie . Kontinentálna redakčná spoločnosť C. Do.
2. Mícheal alebo 'searcoid.(2003) Prvky abstraktnej analýzy ... Oddelenie matematiky. University College Dublin, Beldfield, Dublind.
3. J. Van wyk. (2006) Matematika a inžinierstvo v oblasti informatiky. Inštitút pre počítačové vedy a technológie. Národný úrad pre normy. Washington, D. C. 20234
4. Eric Lehman. Matematika pre počítačovú vedu.  Google Inc.
5. F Thomson Leighton (1980). Počet. Katedra matematiky a technologického inštitútu Massachussetts Institute of Technology Massachussetts.
6. Khanská akadémia. Trojuholníková nerovnosť. Získané z: Khanacademy.orgán
7. Wikipedia. Trojuholníková nerovnosť. Obnovené z: je. Wikipedia.com