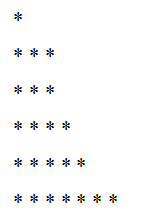Aditívny rozklad

Ten aditívny rozklad kladného celého čísla je vyjadriť ho ako súčet dvoch alebo viacerých pozitívnych čísel. Máme teda toto číslo 5 ho môže vyjadriť ako 5 = 1+4, 5 = 2+3 alebo 5 = 1+2+2. Každý z týchto spôsobov písania čísla 5 je to, čo budeme nazvať aditívnym rozkladom.

Ak venujeme pozornosť, vidíme, že výrazy 5 = 2+3 a 5 = 3+2 predstavujú rovnaké zloženie; Obe majú rovnaké čísla. Avšak iba pre otázku pohodlia sa zvyčajne píše každá z reklám podľa kritérií od najmenej po najväčší.

Aditívny rozklad

Ako ďalší príklad môžeme vziať číslo 27, ktoré ho môžeme vyjadriť ako:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Rozklad aditív je veľmi užitočný nástroj, ktorý nám umožňuje posilniť naše vedomosti o číslovacích systémoch.

Kánonický rozklad

Ak máme počet viac ako dve čísla, konkrétna forma ich rozkladu je v násobkoch 10, 100, 1000, 10 000 atď., ktoré to tvoria. Tento spôsob písania ľubovoľného čísla sa nazýva kanonický aditívny rozklad. Napríklad číslo 1456 ho môže rozložiť takto:

1456 = 1000 + 400+ 50 + 6

Ak máme číslo 20 846 295, váš dekompozícia kánonického aditív bude:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Vďaka tomuto rozkladu vidíme, že hodnota danej číslice je daná pozíciou, ktorú zaberá. Zoberme si príklad čísla 24 a 42:

24 = 20 + 4

42 = 40 +2

Tu vidíme, že v 24 má 2 hodnota 20 jednotiek a na 4 hodnota 4 jednotiek; Na druhej strane, v 42 má 4 hodnota 40 jednotiek a 2 z dvoch jednotiek. Aj keď obidve čísla používajú rovnaké číslice, ich hodnoty sú úplne odlišné podľa pozície, ktorú zaberajú.

Môže vám slúžiť: x na druhú

Žiadosti

Jednou z aplikácií, ktoré môžeme dať k aditívnemu rozkladu, je v určitých typoch demonštrácií, v ktorých je veľmi užitočné vidieť pozitívne celé číslo ako súčet ostatných.

Príklad

Zoberme si ako príklad nasledujúcu vetu s ich príslušnými demonštráciami.

- Byť z celého počtu 4 číslic, potom z je deliteľné 5, ak je jeho obrázok zodpovedajúci jednotkám nula alebo päť.

Demonštrácia

Pamätajme na to, čo je deliteľnosť. Ak máme celé čísla „A“ a „B“, hovoríme, že „„ „delí“ b “, ak existuje celé číslo„ C “, že b = a*c.

Jedna z vlastností deliteľnosti nám hovorí, že ak sú „a“ a „b“ deliteľné medzi „c“, potom je odčítanie „a-b“.

Byť z celého počtu 4 číslic; Preto môžeme napísať na z a z = abcd.

Použitím kanonického rozkladu aditívneho rozkladu musíme:

Z = a*1000 + b*100 + c*10 + d

Je zrejmé, že A*1000 + B*100 + C*10 je deliteľný medzi 5. Preto máme, že z je deliteľné medzi 5, ak z - (a*1000 + b*100 + c*10) je deliteľné medzi 5.

Ale z - (a*1000 + b*100 + c*10) = d a d je jediné číslo obrázku, takže jediný spôsob, ako byť deliteľný medzi 5, je, že je 0 alebo 5.

Preto je z deliteľný medzi 5, ak D = 0 alebo D = 5.

Všimnite si, že ak z má n číslice, demonštrácia je úplne rovnaká, iba sa mení, že by sme teraz napísali z = a₁Do₂.._n A cieľom by bolo dokázať to_n je nula alebo päť.

Oddiely

Hovoríme, že oddiel pozitívneho celého čísla je spôsob, akým môžeme napísať číslo ako súčet pozitívnych celých čísel.

Môže vám slúžiť: Konvergenčné rádio: Definícia, príklady a cvičenia vyriešené

Rozdiel medzi aditívnym rozkladom a oddielom je, že zatiaľ čo v prvom sa hľadá, že sa môže aspoň rozdeliť na dve alebo viac, v oddiele tohto obmedzenia.

Máme teda nasledujúce:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Vyššie uvedené sú oddiely 5.

To znamená, že máme, že všetok rozklad aditív je oddiel, ale nie všetky oddiely sú nevyhnutne aditívny rozklad.

V teórii čísel základná veta aritmetických záruk, že každé celé číslo sa dá napísať jedinečne ako produkt bratrancov.

Keď sa študujú oddiely, cieľom je určiť, koľko spôsobov je možné písať pozitívne celé číslo ako súčet iných celých čísel. Preto definujeme funkciu oddielu, ako je uvedené nižšie.

Definícia

Funkcia oddielu p (n) je definovaná ako počet spôsobov, akými je možné písať pozitívne celé číslo n.

Vráťte sa k príkladu 5, musíme:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

Týmto spôsobom, P (5) = 7.

Grafy

Obidve oddiely a aditívne rozklady čísla n môžu byť znázornené geometricky.  Predpokladajme, že máme aditívny rozklad n. V tomto rozkladu môžu byť dodávateľy opravené tak, aby boli členovia sumy nariadené od najmenej po najväčší. Takže to stojí za to:

n = a₁ + do₂ + do₃ +… + A_r s

do₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_r.

Môžeme grafovať uvedený rozklad nasledovne: V prvom riadku označujeme a₁-body, potom v nasledujúcom označujeme₂-body a tak ďalej, až kým nedosiahnete_r.

Môže vám slúžiť: Nerovnosť trojuholníka: demonštrácia, príklady, vyriešené cvičenia

Zoberme si príklad číslo 23 a jeho ďalší rozklad:

23 = 5 + 4 + 7 + 3 + 1 +3

Objednávame tento rozklad a máme:

23 = 1 + 3 + 3 + 4+ 5 + 7

Jeho zodpovedajúci graf by bol:

Podobne, ak tento graf čítame zvisle namiesto vodorovne, môžeme získať rozklad, ktorý sa pravdepodobne líši od predchádzajúceho. V príklade 23 vyniká toto:

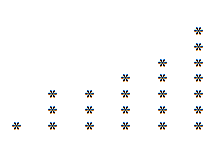
Takže máme, že 23 môžeme napísať aj ako:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.