Implicitné deriváty, ako sú vyriešené a vyriešené cvičenia

Ten implicitné deriváty Sú to nástroje používané v technike diferenciácie, ktorá sa používa na funkcie. Uplatňujú sa, keď to nie je možné, podľa pravidelných metód, vykonávajú odvodenie závislej premennej, ktorá má odvodiť. Táto vôľa sa vykonáva na základe nezávislej premennej.

Napríklad vo výraze 3xy³ - 2y + xy² = xy, nemôžeš dostať výraz, ktorý definuje „y“ v závislosti od „x“. Takže keď je možné získať diferenciálny výraz DY/DX.

[TOC]

Ako sa vyriešia implicitné deriváty?

Na vyriešenie implikácie je založená na implicitnom výraze. Napríklad: 3xy³ - 2y + xy² - Xy = 0. Toto už bolo jasne vyčistené, avšak na to nie je nevyhnutnou podmienkou na získanie derivátu Y týkajúceho sa x. Potom sa každý z prvkov odvodzuje rešpektujúc pravidlo reťazca pre zmiešané funkcie:

3xy³ Pozostáva z 2 premenných, preto D (3xy³) Bude považovaný za derivát produktu funkcií.

D (3xy³)/dx = 3y³ + 3y².(3x) a '= 3y³ + 9xy² a '

Kde je prvok a 'známy ako “a bratranec”A DY/DX predstavuje

-2y sa odvodzuje podľa zákona k.U = k.Alebo '

D (-2y) = -2 a '

Xy² Predpokladá ďalší rozdiel zložený z produktu funkcií

D (XY²) = y² + 2xy a '

-XY je homológny spôsob

d (-xy) = -y -x a '

Sú nahradené rovnosťou, pretože vedia, že nula derivátu je nula.

3y³ + 9xy² a ' - 2 a' + a² + 2xy a ' - y - x a' = 0

Prvky, ktoré majú tento termín a „sú zoskupené na jednej strane rovnosti

Môže vám slúžiť: kolineálne vektory

3y³ + a² - y = -9xy² a ' + 2 a' + x a '

Spoločný faktor a „v pravom členení rovnosti sa extrahuje

3y³ + a² - y = y '(-9xy² + x + 2)

Nakoniec, termín, ktorý sa znásobuje a '. Takže získanie expresie zodpovedajúcej implicitnému derivátu y, pokiaľ ide o x.

a '= dy/dx = (3y³ + a² - y)/(-9xy² + x + 2)

Pravidlo

Pri implicitnej odvodení sa pravidlo reťazca vždy rešpektuje. Všetky diferenciálne výrazy budú uvedené v závislosti od nezávislej premennej x. Aby akákoľvek premenná 9 odlišná od x musí po odvodení zahrnúť termín dθ/dx.

Tento výraz sa objaví iba v prvom stupni alebo s exponentom rovnajúcim sa 1. Táto kvalita je úplne jasná podľa tradičných metód faktorizácie. Takže je možné získať výraz, ktorý definuje diferenciálny dθ/dx.

V pravidle reťazca je uvedená progresívna povaha procesu diferenciácie alebo derivátu. Kde pre akúkoľvek zloženú funkciu f [g (x)] bude musieť byť diferenciálna expresia f

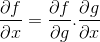
Prevádzkový poriadok

V každom zákone o vzorec alebo odvodení, ktorý sa uplatňuje, sa musí zohľadniť poradie premenných. Kritériá spojené s nezávislou premennou sú rešpektované bez zmeny jej korelácie so závislou premennou.

Pomer závislej premennej v čase odvodeného.; S výnimkou, že sa to bude považovať za druhú funkciu, a preto sa uplatňujú kritériá reťazových pravidiel pre zmiešané funkcie.

Toto sa dá vyvinúť v výrazoch s viac ako 2 premennými. Pod rovnakými zásadami budú všetky rozdiely odkazujúce na závislé premenné.

Môže vám slúžiť: čo je usmernenie? (Geometria)

Graficky sa zaobchádza s rovnakými kritériami, ktoré definujú derivát. Zatiaľ čo derivát je sklon čiary dotyk do krivky v rovine, zvyšok diferenciálov patriacich k závislým premenným (DY/DX, DZ/DX) predstavuje tangenci.

Implicitný funkcia

Hovorí sa, že funkcia je implicitne definovaná, ak výraz y = f (x) môže byť reprezentovaný ako viacnásobná premenná funkcia f (x, y) = 0, zatiaľ čo f je definovaný v rovine r².

3xy³ - 2y + xy² = x a dá sa napísať vo forme 3xy³ - 2y + xy² - Xy = 0

Vzhľadom na nemožnosť vysvetlenia funkcie y = f (x).

História

Diferenciálny počet začal menovať rôzni matematickí vedci okolo sedemnásteho storočia. Prvýkrát, čo sa spomínalo, bolo prostredníctvom príspevkov Newton a Leibniz. Obaja ošetrili diferenciálny počet z rôznych hľadísk, ale zbližovali sa vo svojich výsledkoch.

Zatiaľ čo Newton sa zameriaval na diferenciáciu ako rýchlosť alebo mieru variácie, prístup Leibniz bol geometrický. Dá sa povedať, že Newton zaútočil na domnienky, ktoré zanechal Apollonius z Perge a Leibniz Geometrické myšlienky Fermata.

Implicitné odvodenie sa objaví okamžite, keď zvážia diferenciálne a komplexné rovnice. Rozširovali geometrický koncept Leibniz na r³ a dokonca aj viacrozmerné priestory.

Žiadosti

Implicitné deriváty sa používajú v rôznych situáciách. Sú bežné v problémoch s výmennými kurzmi medzi súvisiacimi premennými, kde sa v závislosti od zmyslu pre štúdium premenné považujú za závislé alebo nezávislé.

Majú tiež zaujímavé geometrické aplikácie, napríklad v problémoch s odrazmi alebo tieňmi, na obrázkoch, ktorých tvar je možné modelovať matematicky.

Môže vám slúžiť: vzorkovanie kvót: Metóda, výhody, nevýhody, príklady

Často využívajú v oblasti hospodárstva a strojárstva, ako aj v rôznych výskumoch prírodných javov a experimentálnych budov.

Vyriešené cvičenia

Cvičenie 1

Definujte implicitný výraz, ktorý definuje DY/DX

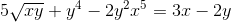
Každý prvok sa líši od výrazu

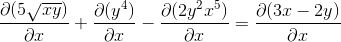
Stanovenie reťazového pravidla v každom kompetentnom prípade

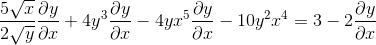
Zoskupenie na jednej strane rovnosti prvky, ktoré majú DY/DX

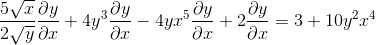
Faktoring pomocou spoločného faktora

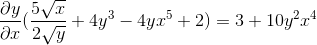
Je vyčistený získaním vyhľadávaného výrazu

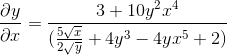
Cvičenie 2

Definujte implicitný výraz, ktorý definuje DY/DX

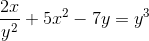
Vyjadrenie derivátov na vykonávanie

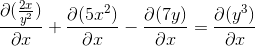
Implicitne odvodenie podľa reťazového pravidla

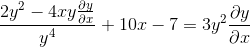
Faktorovanie spoločných prvkov

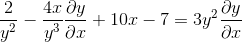
Zoskupenie pojmu dy/dx na jednej strane rovnosti

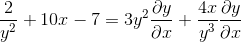
Spoločný faktor diferenciálneho prvku

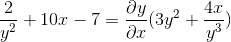
Vyčistíme a získame vyhľadávaný výraz

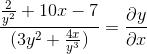
Odkazy

1. Počet jednej premennej. Ron Larson, Bruce H. Edward. Cengage Learning, 10. novembra. 2008
2. Implicitná veta funkcie: história, teória a aplikácie. Steven G. Krantz, Harold R. Parky. Springer Science & Business Media, 9. novembra. 2012
3. Multivariabilná analýza. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. decembra. 2010
4. Dynamika systému: modelovanie, simulácia a riadenie mechatronických systémov. Dekan c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. marca. 2012
5. Kalkul: Matematika a modelovanie. William Bauldry, Joseph R. Fiedler, Frank r.Giordano, Ed Lodi, Rick Vitay. Addison Wesley Longman, 1. januára. 1999