Algebraické deriváty

Čo sú algebraické deriváty?

Ten algebraické deriváty Pozostávajú zo štúdia derivátu v konkrétnom prípade algebraických funkcií. Pôvod pojem derivátov z Derivátu sa datuje do starovekého Grécka. Vývoj tejto predstavy bol motivovaný potrebou vyriešiť dva dôležité problémy, jeden z fyziky a jeden z matematiky.

Vo fyzike derivát rieši problém s určovaním okamžitej rýchlosti pohybujúceho sa objektu. V matematike umožňuje nájsť dotyčničnú čiaru k krivke v danom bode.

Aj keď je skutočne veľa ďalších problémov, ktoré sa riešia pomocou derivátu, ako aj jeho zovšeobecnenia, výsledky, ktoré sa neskôr dostali k zavedeniu ich konceptu.

Priekopníkmi diferenciálneho počtu sú Newton a Leibniz. Predtým, ako poskytneme formálnu definíciu, vyvinieme túto myšlienku, z matematického a fyzického hľadiska.

Derivát ako čaká na dotyčnicu k krivke

Predpokladajme, že graf funkcie y = f (x) je kontinuálny graf (bez hrotov alebo vrcholov alebo separácií) a buď a = (a, f (a)) pevný bod nad ním. Chceme nájsť rovnicu tangensovej čiary s funkciou f v bode a.

Zoberme si ďalší bod p = (x, f (x)) grafu, blízko bodu A, a vysledujte sušenie, ktorá prechádza cez A a P. Suchovacia čiara je čiara, ktorá sa znižuje do grafu krivky do jedného alebo viacerých bodov.

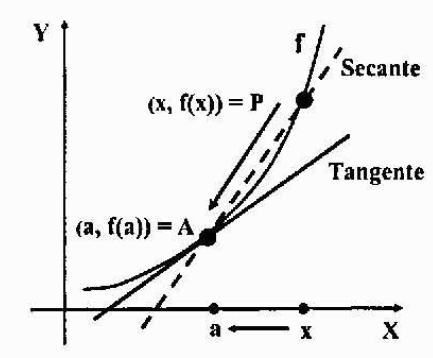
Na získanie dotyčnicovej čiary, ktorú chceme, je potrebné vypočítať iba sklon, pretože už máme bod riadku: bod a.

Ak presunieme bod P v grafe a čoraz viac k nemu pristupujeme k bodu A, predtým uvedená suchá čiara sa priblíži k dotyčnicovej línii, ktorú chcete nájsť. Ak sa uplatňuje limit, keď „P má tendenciu“, obidve čiary sa zhodujú, a preto sa tiež zhodujú ich svahy.

Sklon sekuntnej línie je daný

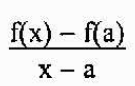
Povedať, že P je blízko A, je rovnocenný s tým, že „X“ sa blíži „A“. Sklon dotyčničnej čiary k grafu F v bode A sa teda bude rovnať:

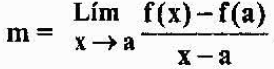
Predchádzajúci výraz je označený f '(a) a je definovaný ako derivát funkcie F v bode „A“. Vidíme, že analyticky je derivát funkcie v bode limit, ale geometricky je to sklon čiary dotyk do grafu funkcie v bode.

Môže vám slúžiť: náhodná premenná: koncept, typy, príklady

Teraz uvidíme túto predstavu z hľadiska fyziky. Dosiahneme rovnaké vyjadrenie predchádzajúceho limitu, hoci inou cestou, čím získame jednomyseľnosť definície.

Derivát ako okamžitá rýchlosť pohybujúceho sa objektu

Pozrime sa na krátky príklad toho, čo znamená okamžitá rýchlosť. Keď sa napríklad hovorí, že auto na dosiahnutie cieľa to urobilo rýchlosťou 100 km za hodinu, čo znamená, že za hodinu cestoval 100 km.

To nevyhnutne neznamená, že počas celej hodiny bolo auto vždy 100 km, v niektorých chvíľach mohol vecimeter automobilu znamenať menej alebo viac. Keby mal potrebu stáť na semafor, rýchlosť v tom okamihu bola 0 km. Avšak po hodine bola trasa 100 km.

To je známe ako priemerná rýchlosť a je daná kvocientom vzdialenosti prejdenej medzi časom uplynulým, ako sme práve videli. Okamžitá rýchlosť je medzitým taká, ktorá označuje rýchlosť automobilu v určitom okamihu (čas).

Pozrime sa na to teraz všeobecnejšie cesty. Predpokladajme, že objekt sa pohybuje pozdĺž čiary a že tento posun je reprezentovaný pomocou rovnice s = f (t), kde premenná t meria čas a premennú s posunom, pričom sa zohľadňuje jeho začiatok t = t = 0, v tom čase je tiež nula, tj f (0) = 0.

Táto funkcia f (t) je známa ako funkcia polohy.

Výraz okamžitej rýchlosti objektu sa vyhľadá v pevnom okamihu. Pri tejto rýchlosti to označíme V (a).

Či už je to okamih blízko k okamžitému „a“. V časovom intervale medzi „a“ a „t“ je zmena polohy daná f (t) -f (a).

Priemerná rýchlosť v tomto časovom intervale je:

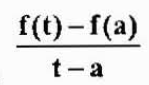
Čo je aproximácia okamžitej rýchlosti V (a). Tento prístup bude lepší, keď sa T dostane bližšie k „a“. Preto,

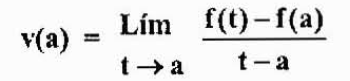
Všimnime si, že tento výraz sa rovná výrazu získaného v predchádzajúcom prípade, ale z inej perspektívy. To je známe ako derivát funkcie F v bode „A“ a je označený f '(a), ako je uvedené vyššie.

Môže vám slúžiť: zákony exponentov

Všimnite si, že vykonanie zmeny h

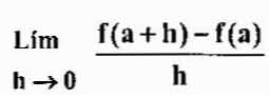
Oba výrazy sú rovnocenné, ale niekedy by sa mali používať viac na jeden namiesto druhého, v závislosti od prípadu.

Potom sa potom definuje všeobecnejšie odvodené z funkcie f v ktoromkoľvek bode „x“ patriace do jeho domény ako

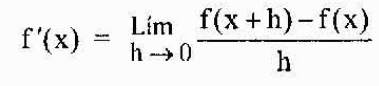
Najbežnejšia notácia, ktorá predstavuje derivát funkcie y = f (x), je tá, ktorú sme práve videli (f 'o y'). Ďalším široko používaným zápisom je však zápis Leibniz, ktorý je znázornený ako ktorýkoľvek z nasledujúcich výrazov:

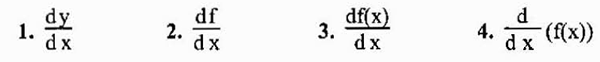
Vzhľadom na skutočnosť, že derivát je v podstate limit, môže alebo nemusí existovať, pretože limity neexistujú vždy. V prípade, že existuje, hovorí sa, že príslušná funkcia je v danom bode diferencovateľná.

Algebraická funkcia

Algebraická funkcia je kombinácia polynómov prostredníctvom sumy, odčítania, produktov, kvocientov, právomocí a radikálov.

Polynóm je vyjadrením formy

P_n= a_nXⁿ+ do_N-1X^N-1+ do_N-2X^N-2+… + A₂X²+ do₁x+a₀

Kde n je prirodzené číslo a všetky_Jo, S i = 0,1, ..., n sú racionálne čísla a_n≠ 0. V tomto prípade sa hovorí, že stupeň tohto polynómu je n.

Nasledujú príklady algebraických funkcií:

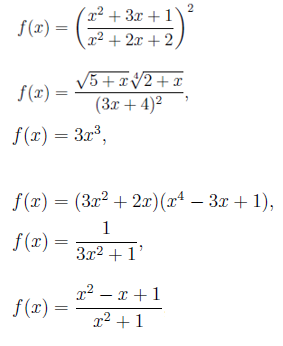
Tu nie sú zahrnuté exponenciálne, logaritmické a trigonometrické funkcie. Pravidlá odvodenia, ktoré uvidíme nižšie, sú platné pre funkcie všeobecne, ale obmedzíme ich a uplatňujeme ich v prípade algebraických funkcií.

Pravidlá

Odvodené z konštanty

Uvádza, že derivát konštanty je nula. To znamená, ak f (x) = c, potom f '(x) = 0. Napríklad derivát konštantnej funkcie 2 sa rovná 0.

Odvodené z moci

Ak f (x) = xⁿ, potom f '(x) = nx^N-1. Napríklad x derivát³ Je 3x². V dôsledku toho sa získa, že odvodená z funkcie identity f (x) = x je f '(x) = 1x^1-1= x⁰= 1.

Ďalším príkladom je nasledujúci: Nech f (x) = 1/x², potom f (x) = x^-2 a f '(x) = -2x^-2-1= -2x^-3.

Táto vlastnosť je tiež platnými koreňmi, pretože korene sú racionálne právomoci a vyššie uvedené je možné použiť aj v tomto prípade. Napríklad odvodený z druhého druhu koreňa je daný

Môže vám slúžiť: odhad prostredníctvom intervalov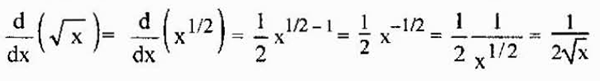

Odvodené zo súčtu a odčítania

Ak sú f a g diferencovateľné funkcie v x, potom je súčet f+g a je splnené, že (f+g) '(x) = f' (x)+g '(x) (x) (x).

Podobne musíte (f -g) '(x) = f' (x) -g '(x). Inými slovami, derivát súčtu (odčítania) je súčet (alebo odčítania) derivátov.

Príklad

Ak h (x) = x²+X-1, potom

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produkt odvodený z produktu

Ak sú f a g diferencovateľné funkcie v x, potom je produkt FG tiež diferencovaný v X a splní sa to

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

V dôsledku toho má, ak C je konštanta a F je diferencovateľná funkcia v x, potom je CF tiež diferencovateľná v x y (cf) '(x) = cf' (x).

Príklad

Ak f (x) = 3x (x²+1), potom

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Odvodené z kvocientu

Ak sú f a g diferencovateľné v x a g (x) ≠ 0, potom f/g je tiež diferencovateľné v x a splní sa to

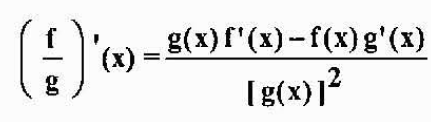
Príklad: Ak h (x) = x³/(X²-5x), potom

H '(x) = [(x³) '(X⁵-5x)-(x³) (X⁵-5x) ']/ (x⁵-5x)²= [(3x²) (X⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Pravidlo

Toto pravidlo umožňuje odvodiť zloženie funkcií. Stanovuje sa nasledujúce: ak je y = f (u) diferencovateľné v u a u = g (x) je diferencovateľné v x, potom je zložená funkcia f (g (x)) diferencovateľná v x a splní sa to [F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F (F G (x))] '= f' (g (x)) g '(x).

To znamená, že derivát zloženej funkcie je produktom derivátu vonkajšej funkcie (vonkajšie deriváty) odvodenou vnútornou funkciou (vnútorný derivát).

Príklad

Ak f (x) = (x⁴-2x)³, tak

f '(x) = 3 (x⁴-2x)²(X⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Existujú tiež výsledky na výpočet konverzného derivátu funkcie, ako aj zovšeobecnenie na deriváty vyššieho poriadku. Aplikácie sú rozsiahle. Medzi nimi sú zvýraznené zisky z optimalizácie a minimálne funkcie.

Odkazy

1. Alarcon, s., González, m., & Quintana, h. (2008). Odlišný počet. Ubytovanie.
2. Cabrera, v. M. (1997). Výpočet 4000. Redakčný progreso.
3. Castaño, h. F. (2005). Matematika pred výpočtom. University of Medellin.
4. Eduardo, n. Do. (2003). Úvod do výpočtu. Utajené vydania.
5. Zdroje, a. (2016). Základná matematika. Úvod do výpočtu. Luk.com.
6. Purcell, e. J., Rigdon, s. A., & Varberg, D. A. (2007). Kalkulácia. Pearson Vzdelanie.
7. Saenz, J. (2005). Odlišný počet (Druhé vydanie.). Barquisimeto: hypotenusa.
8. Thomas, G. B., & Weir, m. D. (2006). Výpočet: niekoľko premenných. Pearson Vzdelanie.