Odvodené od Cotangent Compultution, demonštrácia, cvičenia

Ten Odvodený Sa rovná opakom štvorca úrody „-CSC²„. Tento vzorec je spôsobený derivátovými zákonmi podľa definície a diferenciácie trigonometrických funkcií. Je označovaný takto:

D (ctg u) = -csc² alebo . du

Kde „du“ symbolizuje výraz odvodený z funkcie argumentu, vzhľadom na nezávislú premennú.

Zdroj: Pixabay.com

[TOC]

Ako sa vypočítava?

Postup vývoja týchto derivátov je pomerne jednoduchý. Stačí len identifikovať argument a typ funkcie, ktorú predstavuje.

Napríklad výraz CTG (F/G) predstavuje rozdelenie vo svojom argumente. To bude potrebovať diferenciáciu týkajúcu sa U/V, po rozvoji zipsu.

Cotangent je recipročná funkcia tangens. Algebraicky to znamená, že:

(1/tg x) = ctg x

Ctg x = cos x / sen x

Je nesprávne povedať, že Cotangent Funkcia je „inverzná“ tangens. Je to preto, že inverzná funkcia tangens podľa definície je tangenciálny oblúk.

(TG^-1 x) = arctg x

Podľa Pythagoreanovej trigonometrie je Cotangent zapojený do nasledujúcich častí:

Ctg x = (cos x) / (sin x)

Ctg² X + 1 = CSC² X

Podľa analytickej trigonometrie reaguje na tieto identity:

CTG (a + b) = (1 - tg a . TG B) / (TG A + TG B)

Ctg (a - b) = (1 + tg a . TG B) / (TG A - TG B)

Ctg (2a) = (1 - tg² a) / (2tg a)

Charakteristiky Cotangent funkcie

Je potrebné analyzovať rôzne charakteristiky funkcie f (x) = ctg x, aby bolo možné definovať potrebné aspekty na štúdium jej diferenciácie a aplikácie.

Vertikálne asymptoty

Cotangentná funkcia nie je definovaná v hodnotách, vďaka ktorým je výraz „senx“ nula. Vďaka svojmu ekvivalentnému CTG X = (cos x) / (sin x) bude mať neurčitosť vo všetkých „nπ“, pričom n patrí do celých čísel.

Môže vám slúžiť: analytická geometria

To znamená, v každej z týchto hodnôt x = nπ bude asymptota vertikálny. Keď sa hodnota cotangentných blíži a pri blížení sa práva sa funkcia zvýši na neurčito.

Oblasť

Doména funkcie CotanGent je vyjadrená množinou x ∈ R / x ≠ nπ, n ∈ Z. Toto sa číta ako „x, ktorý patrí do súboru reálnych čísel tak, že x sa líši od nπ, pričom n patrí do celého celého čísla“.

Rozsah

Hodnosť Cotangent Function pokrýva od menej po nekonečno. Preto je možné dospieť k záveru, že jej hodnosť je súbor skutočných čísel N.

Časť

Cotangentná funkcia je periodická a jej perióda sa rovná π. Týmto spôsobom je splnená rovnosť CTG X = CTG (x + nπ), kde n patrí do Z.

Správanie

Je to zvláštna funkcia, pretože ctg (-x) = - ctg x. Týmto spôsobom je známe, že funkcia predstavuje symetriu vzhľadom na súradničný pôvod. Predstavuje tiež zníženie v každom intervale umiestnenom medzi 2 po sebe nasledujúcimi vertikálnymi asymptotmi.

Nemá maximálne alebo minimálne hodnoty, pretože ich prístupy k vertikálnym asymptotom majú správanie, kde funkcia rastie alebo znižuje neurčito.

Nuly alebo korene kolegovej funkcie sa nachádzajú v nepárnych násobkoch π/2. To znamená, že CTG X = 0 sa splní v hodnotách formulára x = nπ/2 s celkovým rozsahom.

Demonštrácia

Existujú 2 spôsoby, ako demonštrovať derivát Cotangent Funkcie.

Trigonometrická diferenciálna demonštrácia

Derivát Cotangent Function je demonštrovaný z jej ekvivalentu v prsníkoch a cosenos.

Môže vám slúžiť: Booleovská algebra: História, vety a postuláty, príklady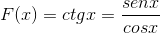

Ide o derivát funkčného rozdelenia

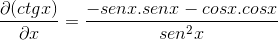
Po odvodení faktorov sú zoskupené a pythagorské identity sa snažia napodobniť

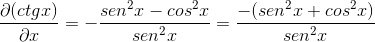
Nahradenie identity a uplatňovanie reciprocity sa získa expresia

Definícia derivátovej definície

Nasledujúci výraz zodpovedá derivátu podľa definície. Kde vzdialenosť medzi 2 bodmi funkcie sa blíži k nule.

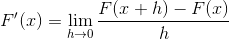
Výmena za Cotangente, ktorú musíte:

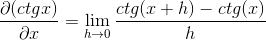
Totožnosti sa vzťahujú na sumu argumentov a reciprocity

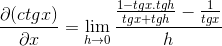
Zlomok čitateľa sa prevádzkuje tradične

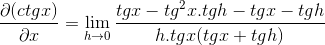
Získava sa eliminovanie opačných prvkov a kreslenie spoločného faktora

Uplatňovanie pythagorských identity a reciprocity

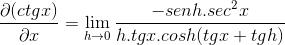
Prvky vyhodnotené v X sú konštantné, pokiaľ ide o limit, preto môžu argumentovať o tom. Potom sa aplikujú trigonometrické limity.

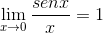
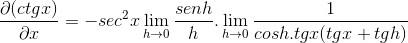
Limit sa hodnotí

Potom sa faktoruje, až kým nedosiahne požadovanú hodnotu

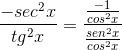
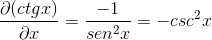
Toto je demonštrované derivátom Cotangente ako opakom štvorca Harvester.

Vyriešené cvičenia

Cvičenie 1

Podľa funkcie f (x) definujte expresiu f '(x)

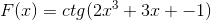
Zodpovedajúca odvodenie sa uplatňuje rešpektujúc pravidlo reťazca

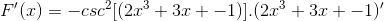
Odvodenie argumentu

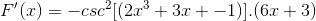
Niekedy je potrebné uplatniť recipročné alebo trigonometrické identity na prispôsobenie riešení.

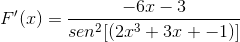
Cvičenie 2

Definujte diferenciálnu expresiu zodpovedajúcu F (x)

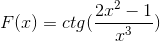
Podľa vzorca derivácie a rešpektovanie pravidla reťazca

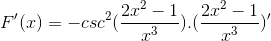
Argument je odvodený, zatiaľ čo zvyšok zostáva rovnaký

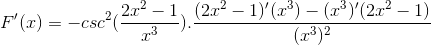
Odvodenie všetkých prvkov

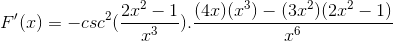
Tradične fungujú výrobky rovnakej základne

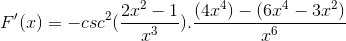
Pridá sa rovnaké prvky a extrahuje sa spoločný faktor

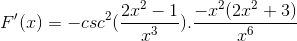
Známky sú zjednodušené a prevádzkované. Ustupovať úplne odvodeným výrazom

Môže vám slúžiť: rozdiel medzi spoločnou frakciou a desatinným číslom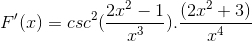

Odkazy

1. Trigonometrická séria, zväzok 1. Do. Zygmund. Cambridge University Press, 2002
2. Počet jednej premennej. Ron Larson, Bruce H. Edward. Cengage Learning, 10. novembra. 2008
3. Počet s trigonometriou a analytickou geometriou. John H. Sasko, John Saxon, Frank Wang, Diana Harvey. Sasxon Publishers, 1988
4. Multivariabilná analýza. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. decembra. 2010
5. Dynamika systému: modelovanie, simulácia a riadenie mechatronických systémov. Dekan c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. marca. 2012
6. Kalkul: Matematika a modelovanie. William Bauldry, Joseph R. Fiedler, Frank r. Giordano, Ed Lodi, Rick Vitay. Addison Wesley Longman, 1. januára. 1999