Pravidelný, nepravidelný decagón, vlastnosti, príklady

On dekačica Je to plochá postava s polygónom s polygónom z 10 strán a 10 vrcholov alebo špičiek. Decagóny môžu byť pravidelné alebo nepravidelné, v prvom prípade majú všetky strany a vnútorné uhly rovnaké opatrenie, zatiaľ čo v druhom druhom stranách a/alebo uhlo.

Obrázok 1 zobrazuje príklady decagónov každého typu a ako vidíme, pravidelný dekagón je veľmi symetrický.

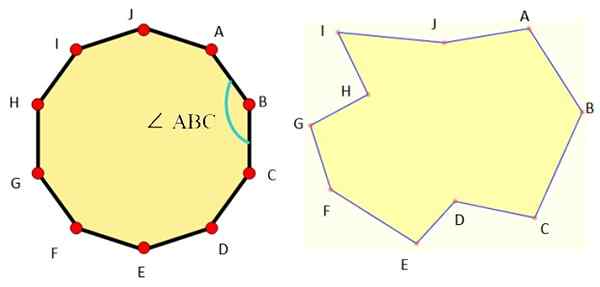postava 1. Vľavo pravidelný decagón a napravo nepravidelný decagón. Zdroj: Wikimedia Commons/F. Zapata/Mathpenref.

Základné prvky všetkých dekagónov sú:

-Strany, segmenty čiary, ktoré pri vstupe do dekagónu.

-Vrcholy alebo body medzi každou nasledujúcou stranou.

-Vnútorné a vonkajšie uhly medzi susednými stranami.

-Diagonály, segmenty, ktoré zjednocujú dva nekontrolované vrcholy.

Vrcholy sa nazývajú kapitálové písmená, ako je znázornené na obrázku 1, kde sa použili prvé písmená abecedy, ale je možné použiť akékoľvek písmeno.

Strany sú symbolizované dvoma písmenami vrcholov, medzi ktorými sú napríklad AB strana, ktorá je medzi vrcholmi A a B. Rovnakým spôsobom sa to robí s diagonálmi, takže máme diagonálny AF, ktorý spája body A a f.

Pre uhly používame tento symbol: ∠, podobne ako sklon l. Napríklad uhol ∠ ABC je ten, ktorého vrchol je B a ktorého strany sú segmenty AB a BC.

[TOC]

Pravidelný dekagón

V pravidelnom dekagóne majú všetky strany rovnaké opatrenie, ako aj vnútorné uhly. Preto sa hovorí rovnocenný (rovnaké strany) a rovný (Rovnaké uhly). Je to veľmi symetrická postava

Interiérové ​​uhly pravidelného dekagónu

Na nájdenie miery vnútorných uhlov pravidelného polygónu vrátane pravidelného dekagónu sa používa nasledujúci vzorec:

Kde:

-I je miera uhla v stupňoch.

-n je počet strán mnohouholníka. V prípade decagónu n = 10.

Môže vám slúžiť: Heptagon

Nahradenie n = 10 v predchádzajúcom vzorci získame nasledujúce:

Teraz sa hovorí, že polygón je vypuklý Ak sú jeho uhlové opatrenia menšie ako 180 °, inak je polygón konkávny. Rovnako ako akýkoľvek vnútorný uhol pravidelných dekagónových opatrení 144 ° a je menší ako 180 °, potom je to konvexný mnohouholník.

Súčet vnútorných uhlov

Súčet opatrení vnútorných uhlov akéhokoľvek polygónu je v stupňoch:

S = (N-2) x 180 °; n je vždy väčší ako 2

V tomto vzorci musíme:

-S je súčet opatrení vnútorných uhlov.

-n je počet strán. Pre dekagón n = 10

Uplatňovanie vzorca pre n = 10 výsledkov:

S = (10 - 2) x 180 ° = 1440 °

Exteriérové ​​uhly 

Vonkajší uhol sa vytvára medzi jednou stranou a predĺžením susednej strany, pozrime sa:

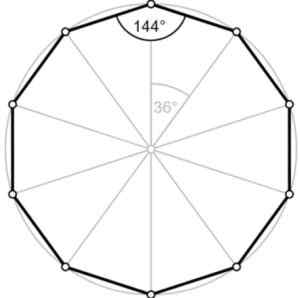
Obrázok 2.- Vonkajší uhol pravidelného dekagónu meria 36 °. Fontána. Wikimedia Commons/F. Zapata.

Uhol ∠ ABC plus vonkajší uhol dodáva 180 °, to znamená, že sú Doplnkový. Preto sa vonkajší uhol rovná 180 °-144 ° = 36 °, ako vidíme na obrázku.

Počet diagonálov

Ako už bolo uvedené, diagonály sú segmenty, ktoré sa spájajú s nekontrolujúcimi vrcholmi. Koľko diagonálov môžeme vysledovať v dekagóne? Ak je počet vrcholov malý, dá sa ľahko spočítať, ale keď sa toto číslo zvýši, môžete stratiť účet.

Našťastie existuje vzorec na poznanie počtu diagonálov, ktoré má polygón n strany:

Pre dekagón nahradíme n = 10 a získame:

D = 10 x (10 - 3) /2 = 35

V pravidelnom dekagóne sú všetky diagonály rezané v jednom bode, čo je stredobodom obrázku:

Obrázok 3. Uhly a diagonály pravidelného dekagónu. Zdroj: Wikimedia Commons.

Stred

Stred polygónu je definovaný ako rovnomerný bod ľubovoľného vrcholu. Na predchádzajúcom obrázku sa centrum zhoduje s bodom križovatky všetkých diagonálov.

Obvod

Ak má pravidelný dekagón stranu A, jeho obvod P je súčtom všetkých strán:

Môže vám slúžiť: 90 deliteľov: Čo sú a vysvetlenie

P = 10.do

Oblasť

Poznanie dĺžky do Pravidelná plocha decagonu sa vypočíta podľa:

Približný vzorec pre túto oblasť je:

A tretia možnosť nájsť oblasť je dĺžkou apothémie l_Do. Toto je segment, ktorý sa pripojí k strede na jednej strane so stredom mnohouholníka.

V tomto prípade sa oblasť môže vypočítať pomocou vzorca:

Nepravidelný dekagón

Nepravidelný decagón nie je rovnostranný alebo rovnomerný a vo všeobecnosti mu chýba symetria pravidelného obrázku, hoci niektoré dekagóny môžu mať os symetrie.

Môžu byť tiež konvexné alebo konkávne, ak existujú vnútorné uhly väčšie ako 180 °.

Nepravidelný decagón na obrázku 1 je konkávny, pretože niektoré z jeho vnútorných uhlov sú väčšie ako 180 °. Je zrejmé, že existuje veľa kombinácií uhlov a strán, ktoré vedú k nepravidelnému dekagónu.

V každom prípade je splnené, že:

-Vnútorné uhly nepravidelného dekagónu tiež pridávajú 1440 °.

-Má tiež 35 diagonálov.

Oblasť nepravidelného decagónu od determinantov Gauss

Všeobecne neexistuje žiadny jedinečný vzorec na nájdenie oblasti nepravidelného polygónu, pretože strany a uhly sú rôzne. Nájdete však poznanie súradníc vrcholov a výpočet Determinanty:

-Zavolajme (x_n , a_n ) do súradníc vrcholov, s n v závislosti od 1 do 10.

-Môžete začať z ľubovoľného vrcholu, ku ktorému budú priradené súradnice (x x₁, a₁ ). Teraz musíte nahradiť hodnoty každej súradnice v tomto vzorci:

Kde determinanty sú presne operácie medzi zátvorkami.

-Je dôležité si uvedomiť, že posledný determinant zahŕňa prvý vrchol spolu s posledným. Pre dekagón by to bolo také:

(X₁₀a₁ - X₁a₁₀)

Môže vám slúžiť: Lagrange Interpolácia

Dôležité: Tyče sú pruhy absolútnej hodnoty a znamenajú, že konečný výsledok je vždy s pozitívnym znamením.

Postup môže byť namáhavý, keď má číslo veľa vrcholov, v prípade dekagónu existuje 10 operácií, takže je vhodné vytvoriť tabuľku alebo zoznam.

Cvičenie

Vypočítajte nepravidelnú plochu dekagónu zobrazenú na obrázku. Súradnice vrcholov sú a, b, c ... j, ktorých hodnoty sú uvedené vľavo.

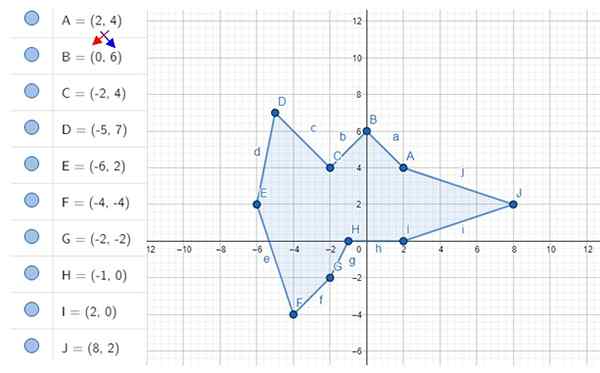Obrázok 4. Nepravidelný dekagón a jeho vrcholy. Zdroj: f. Zapata s geogebou.

Riešenie

-Vykonávame každú z 10 operácií:

• 2 × 6 - 4 × 0 = 12 - 0 = 12
• 0 × 4 - 6 × (-2) = 0 + 12 = 12
• (-2) × 7-4 × (-5) = -14 + 20 = 6
• (-5) × 2 -7 × (-6) = -10 + 42 = 32
• (-6) × (-4) -2 × (-4) = 24 + 8 = 32
• (-4) × (-2)-(-4) × (-2) = 8-8 = 0
• (-2) × 0-(-2) × (-1) = 0 -2
• (-1) × 0 - 0 × (2) = 0 - 0 = 0
• 2 × 2 - 0 × 8 = 4 - 0 = 4
• 8 × 4 -2 × 2 = 32 - 4 = 28

-Pridávame výsledky:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Pozitívny výsledok sa získa aj bez stĺpcov absolútnej hodnoty, ale ak je záporný, to isté sa zmení.

-Predchádzajúci výsledok je vydelený 2 a to je oblasť mnohouholníka:

A = 124/2 = 62

Decangon vlastnosti

Nižšie je zhrnutie všeobecných vlastností dekagónu, či už pravidelné alebo nepravidelné:

-Má 10 strán a 10 vrcholov.

-Súčet vnútorných uhlov je 1440 °.

-Existuje 35 diagonálov.

-Obvod je súčet všetkých strán.

-Môžete vytvárať trojuholníky vo vnútri segmentov kreslenia mnohouholníka zo vrcholu k všetkým ostatným. V dekagóne je možné týmto spôsobom nakresliť 8 trojuholníkov, ako je to znázornené nižšie:

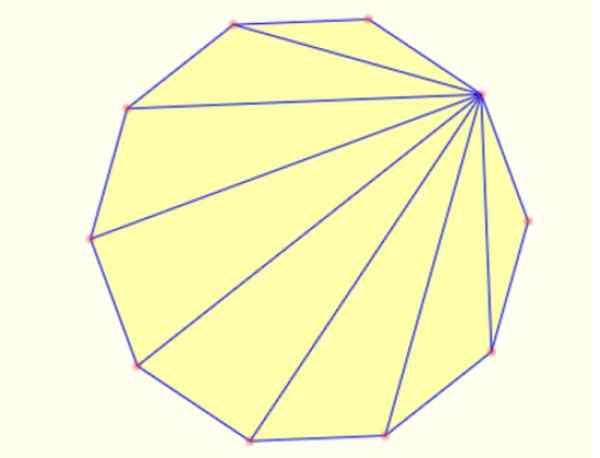Obrázok 5. Vnútorné trojuholníky v pravidelnom dekagóne. Zdroj: Mathpenref.

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Dekačica.com. Dekačica. Získané z: decagon.com
3. Matematika otvorená referencia. Dekačica. Získané z: Mathpenref.com.
4. Matematika. Prvky polygónu a jeho klasifikácie. Získané z: Sangakoo.com.
5. Wikipedia. Dekačica. Obnovené z: je.Wikipedia.com.