Koľko priemerov má obvod?

Obvod má nekonečné priemery. Je ľahké vidieť, že je to tak, ak je založené na definícii priemeru, ktorý je segment, ktorý prechádza súčasne cez stred obvodu a dvoma bodmi toho istého.

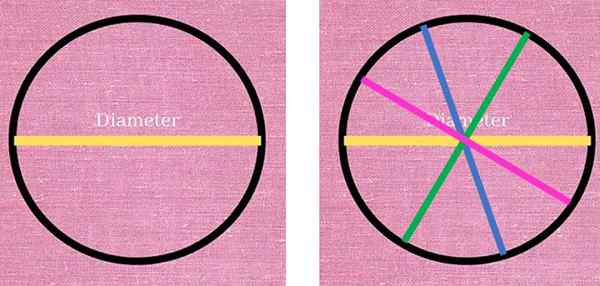
Na nasledujúcom obrázku je vľavo pozorovaná žltá čiara zodpovedajúca priemeru obvodu a rozdelená na dve časti. Na pravej strane boli v rôznych farbách nakreslené ďalšie tri priemery: modrá, zelená a ružová. Všetky majú rovnakú dĺžku a spĺňajú podmienku spojenia dvoch bodov obvodu, cez rovnaké stredisko.

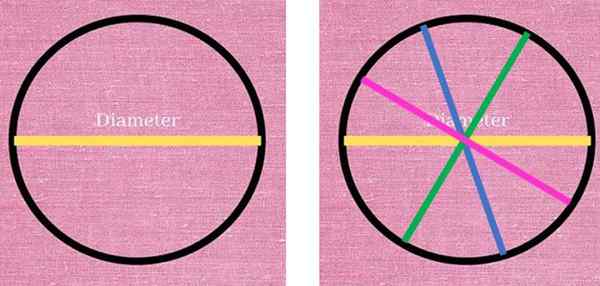Priemer je výrazný segment, ktorý vždy prechádza stredom obvodu a spája dva body tohto bodu. Vľavo, žltý priemer rozdelí obvod na dva. Vpravo existujú ďalšie priemery, ktoré tiež rozdeľujú obvod na dve polovice. Zdroj: f. Zapata.

Ako je vidieť, možnosti kreslenia priemerov sú nekonečné, pretože nekonečné sú body, ktoré tvoria obvod. To isté možno potvrdiť o polomere, ktorý je segmentom, ktorý spája akýkoľvek bod obvodu v strede: je možné nakresliť nekonečný počet rádií.

A pri umiestňovaní dvoch opačných rádií od seba sa získa priemer, pretože polomer meria polovicu tohto.

Priemer, rádio a obvodová dĺžka

Či už je to priemer akéhokoľvek obvodu a R, jeho polomer. Keďže priemer meria dvakrát toľko ako rádio, dá sa napísať:

D = 2 ∙ r

To znamená, že ak polomer kruhu je napríklad r = 5 cm, jeho priemer je d = 2 ∙ 5 cm = 10 cm.

Môže vám slúžiť: Fibonacci Series: Vlastnosti, prírodné vzťahy, aplikácie

Priemer je tiež známy ako Hlavné lano. Reťazce sú čiary alebo segmenty, ktoré sú nakreslené medzi dvoma bodmi obvodu, ale ktoré nemusia nevyhnutne prechádzať stredom. Iba priemer má tento rozdiel.

Na nasledujúcom obrázku môžete vidieť rozdiel a zistiť, prečo je priemer (červený) v skutočnosti najväčší zo reťazcov, ktoré je možné nakresliť na obvod:

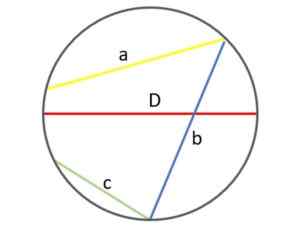Rôzne povrazy v obvode: priemer je najväčší zo všetkých. Zdroj: f. Zapata.

Miera priemeru (a preto polomer) je samozrejme rovnaká v danom obvode. Podľa menenia sa získa menší alebo väčší obvod, podľa.

Na druhej strane sa veľkosť reťazcov toho istého obvodu líši v závislosti od toho, ako ďaleko alebo blízko bodov sú body, ktoré sa spájajú. V zobrazenom príklade je zelené „C“ lano zdanlivo kratšie ako reťazce „A“ a „B“.

A počet reťazcov, ktoré je možné nakresliť, je tiež nekonečný.

Obvod obvodu

Pokiaľ ide o svoju časť, dĺžka obvodu je rovnocenná s jeho obvodom alebo obrysom. Súvisí s jeho priemerom, pretože čím vyšší je, tým väčší je obvod (jeho obvod je väčší).

Pomer alebo kvocient medzi obvodom a priemerom je konštanta nazývaná π (znie „pi“). Hodnota π je 3.141592… Pozastavené body naznačujú, že množstvo desatinných miest a nekonečné, čo je preto, že PI je iracionálne číslo. Avšak na praktické účely môže PI jednoducho zaokrúhliť 3.14

Môže vám slúžiť: Koľko musíte pridať do 3/4, aby ste dostali 6/7?

Ak je obvod označený ako C a priemer ako D, tento dôvod sa vyvoláva takto:

C / d = π

Preto je vzorec pre dĺžku obvodu:

C = π ∙ d

Alebo ak je uprednostňovaný na základe polomeru R:

C = 2π ∙ r

Ilustratívny príklad

Obrázok zobrazuje tri rovnaké obvody, označené písmenami A, B a C. V každom z nich vedie mrav.

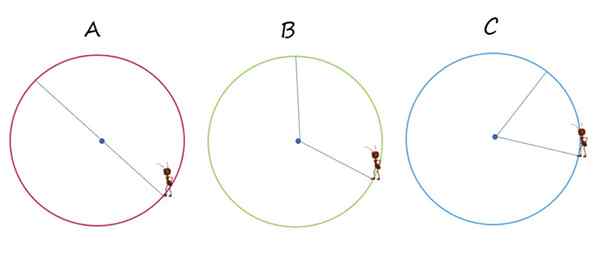Mravec sa pohybuje z jedného bodu do druhého obvodu cez najtenšie modré čiary. Zdroj: f. Zapata.

1.- V ktorom z prípadov k posunu dochádza presne na priemere obvodu?

Odpoveď

Iba v prípade A, pretože táto cesta prechádza stredom obvodu a ide z jedného bodu do druhého z toho istého.

2.- Koľko rádií hmyz cestuje v každom prípade?

Odpoveď

V ktoromkoľvek z týchto troch prípadov mravca cestuje dva rádiá obvodu.

3.- Ktorá z ciest zodpovedá najväčšej vzdialenosti?

Odpoveď

Cesta je v každom prípade rovnako dlhá, čo zodpovedá dvom rádiá obvodu.

4.- V takom prípade je mravec ďalej od východiskového bodu?

Odpoveď

V prípade A, pretože je to v bode, ktorý je presne pred ním, v zostávajúcich, mravec je bližšie k východiskovému bodu.

5.- A v takom prípade mrav?

Môže vám slúžiť: Známky zoskupenia

Odpoveď

V prípade c.

6.- Ak je polomer obvodov 20 cm, koľko centimetrov robí každú cestu?

Odpoveď

Pretože mravec prevádzkuje vzdialenosť rovnajúcu sa dvom rádiá, celková vzdialenosť je 40 cm.

Vyriešené cvičenia

Cvičenie 1

Vypočítajte polomer kruhu, ktorého priemer je 4.5 m.

Riešenie

Rádio je polovica priemeru, ak sa to meria 4.5 cm, potom rádio R je 2.25 cm.

Cvičenie 2

Nájdite obvod obvodu cvičenia 1.

Riešenie

Obvod sa vypočíta priemerom alebo cez polomer, ako je preferované. V prvom prípade:

C = π ∙ d

Za predpokladu, že π = 3.14, nahradenie hodnôt dáva nasledujúci výsledok:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Cvičenie 3

Od dizajnéra sa žiada, aby nakreslil logo so srdcom, s rozmermi uvedenými na obrázku. Zakrivené časti zodpovedajú presným polkruhom.

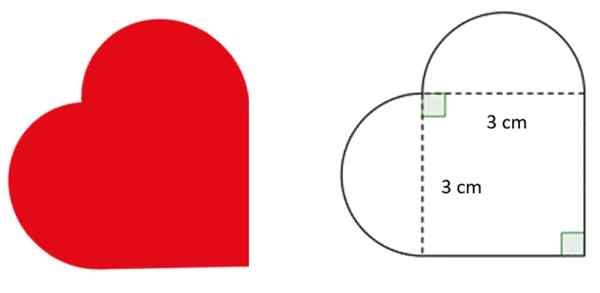
S touto informačnou odpoveďou:

1. Aký je polomer polruhov?
2. Koľko stojí obvod srdca?

Roztok

Priemer polruhov je rovnocenný s bokom štvorca, čo je 3 cm. Preto jeho polomer, ktorý je polovica, meria 1.5 cm.

Riešenie B

Obvodom srdcovej postavy je súčet dvoch vonkajších strán štvorca a obvodom polounancií. Rovnako ako identický, jeho obvod sa rovná obvodu kompletného kruhu s priemerom 3 cm:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Preto obvod P obrázku je:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm