Koľko je x od x?

Vynásobiť x x x dostanete x².

X² znie ako “X na druhú„Alebo jednoducho“X na druhú„.

Prečo x x x je x²?

Výsledok X od X je X².

Vďaka Vlastnosť násobenia právomocí rovnakej bázy.

V algebre sa písmeno X používa ako spôsob, ako nazvať sumu, ktorá má neznáme hodnoty, hoci je možné použiť aj iné písmená.

Vlastnosť násobenia právomocí tej istej základne uvádza, že “Pri vynásobení dvoch rovnakých základní je napísaná rovnaká základňa a pridávajú sa exponenty„.

X^do∙ x^b = x^A+B

Exponent rovný 1 z x je zvyčajne vynechaný, takže X¹ = x.

Ak chceme vedieť, koľko x od x:

Ten Základňa je x (to isté je napísané) a Exponenty sa pridávajú do+B (Jeho hodnoty sa rovnajú 1):

x ∙ x = x¹⁺¹ = x²

Príklady majetku násobenia právomocí rovnakej bázy

Pozrime sa na niektoré veľmi jednoduché numerické príklady:

2 × 2 = 2² = 4

3 × 3 = 3² = 9

4 × 4 = 4² = 16

(−2) × (−2) = 2² = 4

Všimnite si, že vyššie uvedený záporný znak nemení výsledok, pretože podľa zákona o príznakoch sa vynásobí dve záporné sumy kladné výsledky.

V predchádzajúcich príkladoch sa použili celé čísla, ale operácia je rovnako platná pre desatinné, frakčné, skutočné a zložité čísla.

Oblasť štvorca

Štvorcový počet sa často objavuje vo výpočte oblastí pravidelných geometrických čísel. Napríklad štvorec, ktorý je jediným štyri polygónom, ktorý má rovnaké opatrenie.

Môže vám slúžiť: Systém rovníc: Metódy riešenia, príklady, cvičenia

Oblasť štvorca je daná štvorcom jeho strany, ak sa nazýva „x“, potom oblasť A štvorca stojí za x².

Príklad oblasti štvorca

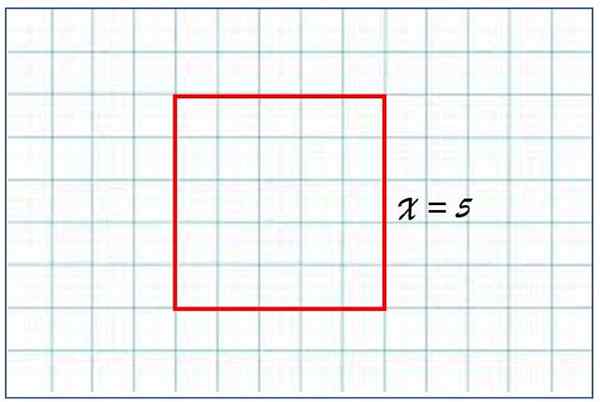
Štvorcová plocha A, ktorej strana je x = 5 jednotiek sa rovná:

A = 5² = 5 × 5 = 25 jednotiek oblasti

Štvorec na strane rovnajúce sa 5 ľubovoľným jednotkám s dĺžkou má rozlohu 25 jednotiek plochy. Zdroj: f. Zapata.

Tento výsledok má zmysel, pretože námestie pozostáva z 5 riadkov a 5 stĺpcov menších štvorcov, zo strany rovnajúce sa 1. Ak čitateľ pozorne sleduje postavu, uvedomí si, že červené štvorec pozostáva z 25 malých štvorcov jednotnej oblasti.

Dôležité:

Jednotky v tomto príklade sú svojvoľné, môžu byť merače, centimetre, palce alebo iné. Tu neboli špecifikované, ale v žiadnom prípade by bola príslušná oblasť podaná v metroch štvorcových, štvorcových palcov alebo iných. Táto oblasť je vždy uvedená v jednotkách štvorcovej dĺžky.

Štvorec frakčných a desatinných čísel

Ak chcete nájsť štvorec frakčného čísla, ktoré pozostáva z očíslovaného a menovateľa oddeleného frakčným riadkom, je potrebné vynásobiť čitateľa samotným, ako aj menovateľom, ktorý získa nové frakčné číslo.

Príklady štvorcových štvorcov

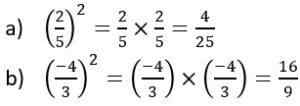
Príklady štvorcových čísel

Pokiaľ ide o štvorec desatinného čísla, musíme dodržiavať pravidlá násobenia pre desatinné čísla.

a) 0.6² = 0.6 × 0.6 = 0.36

b) (−0.4)² = (−0.4) × (−0.4) = 0.16

V tomto príklade aj v zodpovedajúcej jednej z predchádzajúcich oddielov sa pozoruje, že štvorec záporného čísla je vždy pozitívny. To platí pre rovnomerné sily, nielen pre štvorec.

Môže vám slúžiť: ekvivalentné sady: Čo sú, vysvetlenie, príklady