Kritériá podobné trojuholníky

Aké sú kritériá podobnosti trojuholníkov?

Kritériá podobnosti trojuholníkov sú pravidlá, ktoré umožňujú vedieť, či sú dva trojuholníky podobné. Podobnosť geometrických čísel, vrátane trojuholníkov, vyžaduje, aby tieto čísla mali rovnaký spôsob, hoci nemusia mať nevyhnutne rovnakú veľkosť alebo rovnakú orientáciu.

Aby boli dva trojuholníky podobné, je potrebné, aby: i) ich homológne strany sú proporcionálne a ii) vnútorné uhly každého z nich majú rovnaké opatrenie.

postava 1. Dva podobné trojuholníky: Aj keď nemajú rovnakú veľkosť, ich strany sú proporcionálne a ich vnútorné uhly majú rovnakú mieru. Zdroj: f. Zapata.

Pomerný pomer alebo pomer medzi dvoma množstvami A a B je predstavovaný pomerom A/B, s b ≠ 0. Pokiaľ ide o podobné trojuholníky, sú platné nasledujúce rozmery medzi ich stranami:

a/a '= b/b' = c/c '= r

Hodnota R sa volá dôvod.

Okrem toho musia byť zodpovedajúce vnútorné uhly rovnaké, preto: ∠A = ∠A '; ∠B = ∠B 'a ∠C = ∠C'. Podľa týchto podmienok sú kritériá podobnosti trojuholníkov:

Kritériá 1: Dva trojuholníky sú podobné, ak majú dva vnútorné uhly rovnakej miery. Ak áno, tretí uhol tiež meria to isté, pretože súčet vnútorných uhlov v akomkoľvek trojuholníku je 180 °:

a = α '; β = β '

Kritériá 2: Trojuholníky sú podobné, ak sú dve homológne strany úmerné a uhol medzi nimi je rovnaký:

a/a '= b/b'; α = α '

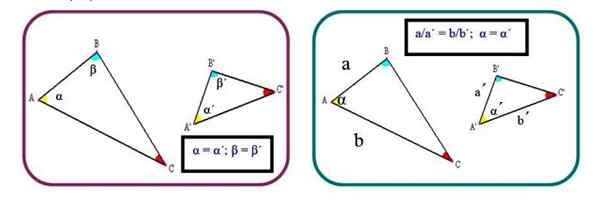Obrázok 2. Dve kritériá na stanovenie podobnosti trojuholníkov. Zdroj: f. Zapata.

Kritériá 3: Tri homológne strany sú úmerné:

a/a '= b/b' = c/c '= r

Príklady

Podobnosť trojuholníkov je veľmi užitočná na výpočet výšok a vzdialeností, ktoré nie sú ľahko merateľné priamo. Prostredníctvom niektorých jednoduchých výpočtov je možné zistiť tieto dĺžky porovnaním podobných trojuholníkov.

Môže vám slúžiť: Základná veta aritmetiky: demonštrácia, aplikácie, cvičenia

Výška stĺpcov, budov a stromov

Hovorí sa, že otec geometrie v starovekom Grécku, napríklad Miletus (625-547 až.C.), vypočítaná výška stĺpca chrámu bez potreby špeciálnych nástrojov, jednoducho porovnaním dĺžky tieňa jeho trstiny s výškou stĺpca a použitím podobnosti trojuholníkov. Rovnakým spôsobom sa mu podarilo zmerať výšku Veľkej pyramídy Egypta, a tak zapôsobiť na faraóna.

Vzdialenosť od Mesiaca

Existuje jednoduchý experiment, ktorý sa vykonáva na výpočet vzdialenosti medzi Zemou a mesiacom. Vyžaduje si menu, trochu lepiacej pásky a vernier alebo pravidlo absolventov. Keď je mesiac plný, mena je pripevnená k sklu okna a mesiac je pozorovaný jedným okom, ktorý sa nachádza takým spôsobom, že mena pokrýva iba splnu mesiac.

Keď sa to stane, dôvod medzi priemerom meny a vzdialenosťou medzi okom a menou je rovnaký, že existuje medzi priemerom mesiaca a vzdialenosťou medzi okom a mesiacom:

Priemer meny/mena vzdialenosti = priemer mesiaca/vzdialenosť od mesiaca

Dôvod je približne 1/110. Čo znamená, že vzdialenosť od mesiaca je 110 -násobok priemeru tohto.

V súčasnosti sa polomer mesiaca odhaduje v roku 1737.1 km, takže jeho priemer je 3474.2 km. Nahradením tejto hodnoty vo vzťahu:

Vzdialenosť od mesiaca = priemer mesiaca ÷ (priemer meny/vzdialenosť od meny)

Je získané:

Vzdialenosť od Mesiaca = 3474.2 km ÷ (1/110) = 382.162 km

Môže vám to slúžiť: hepagonálny hranol

Veľmi blízko k hodnote stanovenej 384 astronómom.000 km.

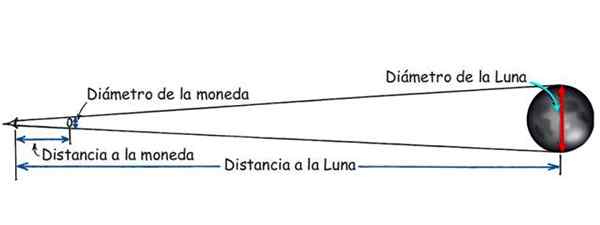Obrázok 3. Vzdialenosť od Mesiaca môže byť známa vďaka podobnosti trojuholníkov. Zdroj: Upravené Hewitt, P. Koncepčná fyzika.

Vzdialenosť medzi loďou a pobrežím

Na meranie vzdialenosti medzi loďou a pobrežím sa podiely uviaznú na pláži v bodoch A, B, C a Q. ABC a PCQ trojuholníky sú podobné podľa kritérií 1, pretože majú dva rovnaké uhly: dva uhly ∠C = α, ktoré sú proti vrcholu a dva priame uhly rovné 90 °: ∠B = ∠Q.

Dva trojuholníky sa nachádzajú týmto spôsobom, o ktorých sa hovorí, že sú v Poloha A vždy sú podobné. Trojuholníky sú identifikované v polohe Thales, aby mali spoločný uhol a opačné strany v tomto uhle sú rovnobežné.

V ďalšej časti je cvičenie s číselnými hodnotami.

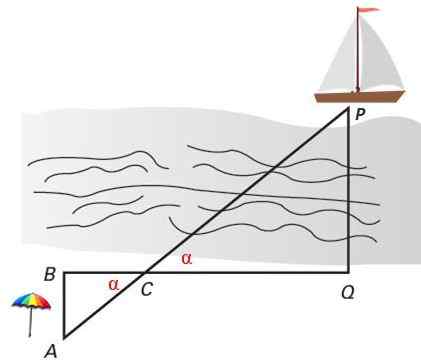Obrázok 4. Dva podobné trojuholníky v polohe Thales slúžia na výpočet kolmej vzdialenosti lode na pobrežie. Zdroj: f. Zapata.

Vyriešené cvičenia

Cvičenie 1

Chcete zistiť, ako ďaleko je plachetnica ukotvená na predchádzajúcej postave, z bodu, ktorý sa nachádza na brehu pláže, pre ktorý sú stávky pribité v bodoch A, B, C a Q, čím určujú trojuholník ABC, ktoré je podobný PCQ, ale ktorých strany sa dajú ľahšie merať.

Vypočítajte kolmo PQ medzi loďou a pobrežím podľa podobnosti trojuholníkov, ak sú dostupné vzdialenosti:

AB = 12 m

BC = 16 m

QC = 60 m

Riešenie

Proporcie medzi homológnymi stranami sú:

Ab/qp = bc/cq = 16 m/60 m = 0.267

Preto 0.267 je dôvodom podobnosti:

AB/QP = 0.267

QP = AB / 0.267 = 12 m / 0.267 = 44.9 m

Cvičenie 2

V nasledujúcom trojuholníku: Koľko meria segment reklamy?

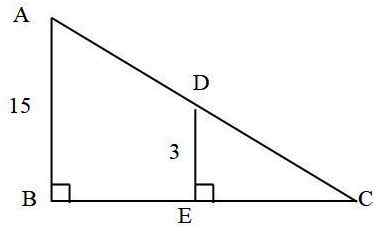
Je to známe, že:

• AC = 25 cm
• AB = 15 cm
• De = 3 cm

Môže vám slúžiť: násobky 2: Čo sú a vysvetlenie

Riešenie

Trojuholníky sú podobné, pretože zdieľajú uhol, ktorý je ∠C a boky a ab sú rovnobežné. Pomer podobnosti sa počíta:

R = ab / de = 15 cm / 3 cm = 5

A tiež cez:

R = ac / dc

Preto DC = AC / R = 25 cm / 5 = 5 cm

Od:

AC = AD + DC

Z toho vyplýva, že AD = AC - DC = 25 cm - 5 cm = 20 cm

Cvičenie 3

Isosceles trojuholník má obvod 49 cm a základňu 21 cm. Vypočítajte obvod trojuholníka podobného tomu, ale ktorého základňa meria 4 cm.

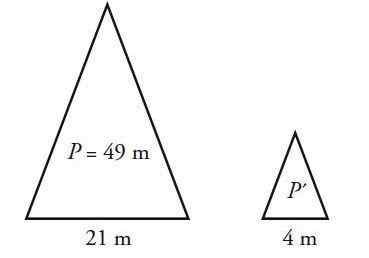
Riešenie

Isosceles trojuholník má dve rovnaké strany, odlišné od základne B. Nech ℓ miera strany a obvodu, ktorý pozostáva zo súčtu troch strán. Pre najväčší trojuholník:

P = 2 ℓ + b = 49 cm

2 ℓ + 21 cm = 49 cm → ℓ = (49-21) cm / 2 = 14 cm

Teraz je vyzdvihnutý pomer medzi stranymi trojuholníkov, ktoré sú symbolizované prémiou:

B/ b '= ℓ/ ℓ'

21 cm / 4cm = 14 cm / ℓ '→ ℓ' = 14 cm / (21 cm / 4cm) = 2.67 cm

Obvod malého trojuholníka bude:

P '= 2 ℓ' + b '= (2 x 2.67) cm + 4 cm = 9.33 cm.

Odkazy

1. Alexander, D. 2013. Geometria. 5. Vydanie. Učenie sa.
2. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5. Edimatizovať. Pearson.
3. Clemens, s. Geometria s aplikáciami. Addison Wesley.
4. Ibáñez, P. 2010. Matematika III. Učenie sa.
5. Jiménez, r. Matematika II: Geometria a trigonometria. Druhý. Vydanie. Pearson.
6. Stewart, J. 2007. Predbežné vyfarbenie. 5. Vydanie. Učenie sa.
7. Vicmat. Samos Aristarco: Opatrenia slnečnej sústavy. Získané z: Vicmat.com