Primeranosť konštanta, čo je, výpočet, cvičenia

Ten primeranosť Je to relačný numerický prvok, ktorý sa používa na definovanie vzoru podobnosti medzi dvoma veľkami. Je veľmi bežné, že ho reprezentuje ako všeobecná lineárna funkcia prostredníctvom výrazu f (x) = k.X. Toto však nie je jediné znázornenie možnej proporcionality.

Napríklad vzťah medzi x a y vo funkcii y = 3x má konštantu proporcionality rovnajúce sa 3. Ukazuje, že keď rastie nezávislá premenná X, tak aj závislá premenná a v trojnásobku svojej predchádzajúcej hodnoty.

Zmeny aplikované v jednej premennej, majú na druhej strane okamžité následky, takže existuje hodnota známa ako konštanta proporcionality. Toto slúži na spojenie rôznych veľkostí, ktoré obe premenné získavajú.

[TOC]

Aká je konštanta proporcionality a typov

Podľa trendu v zmene premenných je možné proporcie klasifikovať do 2 typov.

Priama proporcionalita

Naznačuje jednosmerný vzťah medzi dvoma veľkami. V ňom, ak nezávislá premenná predstavuje určitý rast, závislá premenná tiež rastie. Podobne akékoľvek zníženie nezávislej premennej spôsobí zníženie rozsahu a.

Napríklad lineárna funkcia použitá v úvode; Y = 3x, zodpovedá priamemu pomeru proporcionality. Dôvodom je, že zvýšenie nezávislej premennej X spôsobí zvýšenie trojnásobku v predchádzajúcej hodnote, ktorú vzniesla závislá premenná a.

Podobne závislá premenná zníži trojnásobnú svoju hodnotu, keď X zostúpi do veľkosti.

Hodnota proporcionálnej konštanty „k“ v priamom vzťahu je definovaná ako k = y/x.

Inverzná alebo nepriama proporcionalita

V tomto type funkcií je vzťah medzi premennými prezentovaný antonymovým spôsobom, kde rast alebo zníženie nezávislej premennej zodpovedá poklesu alebo rastu závislej premennej.

Môže vám slúžiť: rozklad prírodných čísel (príklady a cvičenia)

Napríklad funkcia f (x) = k/x je inverzný alebo nepriamy vzťah. Pretože hodnota nezávislej premennej sa začína zvyšovať, hodnota K bude vydelená rastúcou hodnotou, čím sa zníži závislá premenná hodnota podľa pomeru.

Podľa hodnoty prijatej K je možné definovať tendenciu proporcionálnej inverznej funkcie. Ak k> 0, funkcia sa zníži vo všetkých reálnych číslach. A jeho graf sa bude nachádzať v 1. a 3. kvadrante.

Naopak, ak je hodnota k záporná alebo menšia ako nula, funkcia sa zvýši a jej graf sa nachádza v 2. a 4 kvadrante.

Ako sa vypočítava?

Existujú rôzne kontexty, v ktorých sa môže vyžadovať definícia konštanty proporcionality. V rôznych prípadoch sa ukážu rôzne údaje o probléme, kde ich štúdia konečne ukáže hodnotu K.

Všeobecne sa môžu spomenuté rekapitovať. Hodnoty K zodpovedajú dvom výrazom podľa typu prítomného proporcionality:

- Priamy: k = y/x

- Inverzné alebo nepriame: k = y.X

Podľa vášho grafu

Niekedy bude známy iba graf funkcie čiastočne alebo úplne. V týchto prípadoch bude potrebná grafická analýza typ proporcionality. Potom budeme musieť definovať súradnicu, ktorá umožní overiť hodnoty x a y, aby sa použila na zodpovedajúci vzorec K.

Grafy odkazujúce na priame proporcie sú lineárny typ. Na druhej strane grafy inverzných proporcionálnych funkcií zvyčajne majú tvar hyperboly.

Podľa tabuľky hodnôt

V niektorých prípadoch existuje tabuľka hodnôt s hodnotami zodpovedajúcimi každej iterácii nezávislej premennej. Normálne to znamená realizáciu grafu okrem definovania hodnoty k.

Môže vám slúžiť: Distribúcia frekvencie: Ako vytvoriť tabuľku, napríklad cvičenie

Podľa analytického výrazu

Ukazuje výraz, ktorý definuje analyticky. Priamo hodnota K môže byť jasná, alebo sa dá odvodiť aj zo samotného výrazu.

Spravidla troch priamych alebo zlúčenín

V iných cvičebných modeloch existujú určité údaje, ktoré sa vzťahujú na vzťah medzi hodnotami. To je potrebné uplatniť tri priame alebo zlúčeniny na definovanie ďalších potrebných údajov v roku.

História

Koncept proporcionality bol vždy prítomný. Nielen v mysli a práci veľkých matematikov, ale aj v každodennom živote populácie, kvôli ich praktickosti a uplatniteľnosti.

Je veľmi bežné splniť situácie, ktoré si vyžadujú prístup proporcionality. Tieto sú uvedené v každom prípade, keď sa porovnávajú premenné a javy, ktoré udržiavajú určité vzťahy.

Prostredníctvom časovej osi môžeme charakterizovať historické momenty, v ktorých sa uplatnili matematický pokrok týkajúci sa proporcionality.

- Druhé storočie a.c. Skladovací systém frakcií a proporcií v Grécku je prijatý.

- 5. storočie a.c. Podiel, ktorý sa týka strany a diagonálu štvorca, sa objavuje aj v Grécku.

- 600 a.c. Tales de Mileto predstavuje svoju vetu týkajúcu sa proporcionality.

- Rok 900. Desatinný systém, ktorý predtým používa India, sa rozširuje. Príspevok Arabov.

- Xvii storočie. Príspevky sa vzťahujú na proporcie pri výpočte príchodu Eulera.

- Storočie XIX. Gauss poskytuje koncept komplexného počtu a proporcie.

- Dvadsiate storočie. Proporcionalita ako funkčný model je definovaný cukrom a deulofeom.

Vyriešené cvičenia

Cvičenie 1

Vyžaduje sa na výpočet hodnoty premenných x, y, z a g. Poznanie nasledujúcich proporcionálnych vzťahov:

3x + 2y - 6z + 8g = 1925

Môže vám slúžiť: Kontinuálna náhodná premenná

x/3 = y/8 = z/3 = g/5

Sú definované relatívne hodnoty konštanty proporcionality. Dajú sa získať z druhého vzťahu, kde hodnota, ktorá rozdeľuje každú premennú, naznačuje vzťah alebo dôvod týkajúci sa k.

X = 3k y = 2k z = 3k g = 5k

Hodnoty sa nahradia v prvom výraze, kde sa nový systém vyhodnotí v jednej premennej K.

3 (3K) + 2 (2k) - 6 (3k) + 8 (5k) = 1925

9k + 4K -18k + 40k = 1925

35k = 1925

K = 1925/35 = 55

Pri použití tejto hodnoty konštantnej proporcionality nájdeme číslo, ktoré definuje každú z premenných.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Cvičenie 2

Vypočítajte konštantu proporcionality a výraz, ktorý definuje funkciu, vzhľadom na jej grafiku.

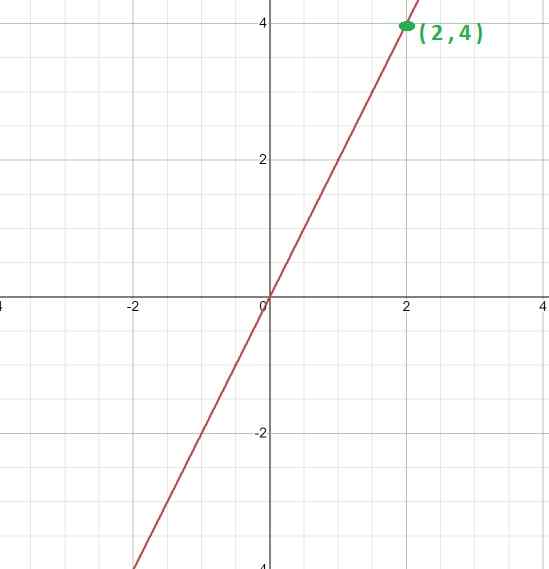
Po prvé, graf sa analyzuje, pričom jeho lineárny znak je zrejmý. To naznačuje, že ide o funkciu s priamou proporcionálnou a že hodnota K sa získa výrazom k = y/x

Potom je vybraný určený bod grafu, to znamená ten, v ktorom súradnice, ktoré ho skladajú, môžu byť presné.

V tomto prípade sa tento bod odoberie (2, 4). Kde môžeme nadviazať nasledujúci vzťah.

K = 4/2 = 2

Takže výraz je definovaný funkciou y = kx, ktorá bude v tomto prípade

F (x) = 2x

Odkazy

1. Matematika pre elektrinu a elektroniku. DR. Arthur Kramer. Cengage Learning, 27. júla. 2012
2. Vision 2020: Strategická úloha prevádzkového výskumu. N. Ravichandran. Spojenecní vydavatelia, 11. september. 2005
3. Gramatické a aritmetické znalosti štátneho administratívneho asistenta.elektronická kniha. Šialené vzdelávanie
4. Matematika posilnenia pre podporu a diverzifikáciu kurikulárnych osnov: pre podporu a diverzifikáciu kurikulárnych osnov a diverzifikácia. Mª Lourdes Lázaro Soto. Narcea Ediciones, 29. augusta. 2003
5. Logistika a komerčné riadenie. Maria José Escudero Serrano. Paraninfo Editions, S.Do., 1. september. 2013