Obdĺžnikové komponenty vektora (s cvičeniami)

Ten obdĺžnikové komponenty vektora sú údaje, ktoré tvoria tento vektor. Na ich určenie je potrebné mať súradnicový systém, ktorým je zvyčajne karteziánska rovina.

Akonáhle budete mať vektor v súradnicovom systéme, jeho komponenty sa môžu vypočítať. Sú to 2, horizontálna zložka (rovnobežná s osou x), nazývaná „zložka v osi x“ a vertikálna zložka (rovnobežná s osou y), nazývaná „komponent v osi y“ “.

Grafické znázornenie obdĺžnikových komponentov vektora

Na určenie komponentov je to potrebné.

[TOC]

Ako určiť obdĺžnikové komponenty vektora?

Na určenie týchto komponentov musia byť známe určité vzťahy medzi obdĺžnikmi a trigonometrickými funkciami.

Na nasledujúcom obrázku môžete vidieť tento vzťah.

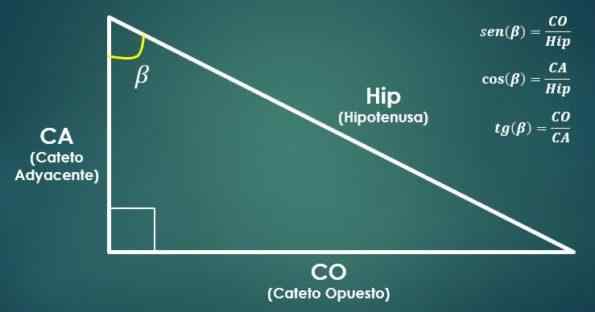Vzťahy medzi obdĺžnikmi a trigonometrickými funkciami

Bosom uhla sa rovná kvocientu medzi mierou kateto na rozdiel od uhla a miera hypotenusu.

Na druhej strane sa kosínus uhla rovná kvocientu medzi mierou kateta susediaceho s uhlom a miera hypotenusu.

Tangent uhla sa rovná kvocientu medzi mierou opačnej nohy a mierou susedného kateta.

Vo všetkých týchto vzťahoch je potrebné stanoviť zodpovedajúci obdĺžnikový trojuholník.

Existujú aj iné metódy?

Jo. V závislosti od poskytnutých údajov sa spôsob výpočtu obdĺžnikových komponentov vektora môže meniť. Ďalším nástrojom, ktorý sa používa veľa, je veta Pythagoras.

Môže vám slúžiť: Existencia a jedinečnosť veta: demonštrácia, príklady a cvičenia

Vyriešené cvičenia

Nasledujúce cvičenia uvádzajú do praxe definíciu obdĺžnikových komponentov vektora a vyššie uvedené vzťahy.

Prvé cvičenie

Je známe, že vektor A má veľkosť rovná 12 a uhol, že táto forma s osou x má 30 ° opatrenie. Určiť obdĺžnikové komponenty uvedeného vektora.

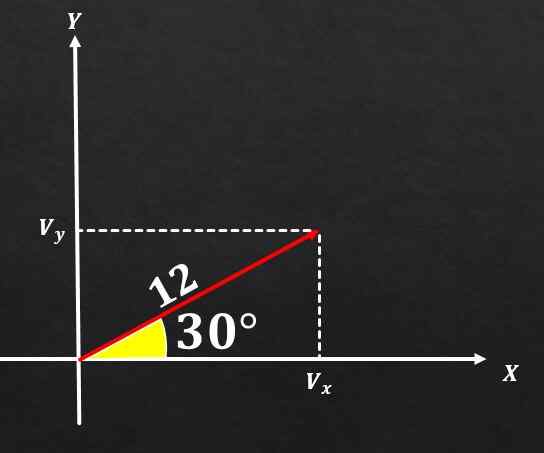
Riešenie

Ak je obrázok ocenený a použité vzorce opísané vyššie, je možné dospieť k záveru, že komponent v a vektore A sa rovná

Sin (30 °) = Vy / 12, a preto vy = 12*(1/2) = 6.

Na druhej strane, komponent na osi x vektora A sa rovná

cos (30 °) = vx / 12, a teda Vx = 12*(√3 / 2) = 6√3.

Druhé cvičenie

Ak má vektor A veľkosť rovnajúcu sa 5 a komponent na osi x sa rovná 4, určte hodnotu komponentu A na osi y.

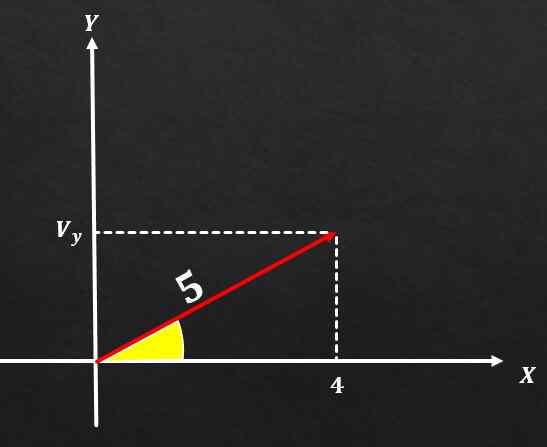
Riešenie

Pomocou vety Pythagory musí byť veľkosť vektora vysoký štvorcový súčet štvorcov dvoch obdĺžnikových komponentov. To znamená m² = (vx) ² + (vy) ².

Nahradenie poskytnutých hodnôt musíte

5² = (4) ² + (vy) ², preto 25 = 16 + (Vy) ².

To znamená, že (vy) ² = 9 a následne vy = 3.

Tretie cvičenie

Ak má vektor A veľkosť rovná 4 a tento uhol 45 ° s osou x, stanovte obdĺžnikové komponenty uvedeného vektora.

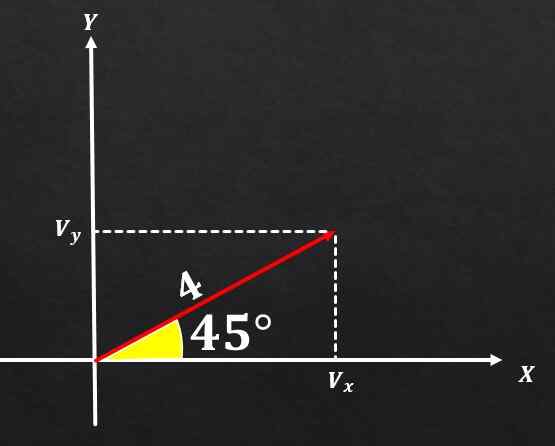
Riešenie

Použitím vzťahov medzi obdĺžnikovým trojuholníkom a trigonometrickými funkciami je možné dospieť k záveru, že komponent na a vektor A sa rovná

Sin (45 °) = vy / 4, a preto vy = 4*(√2 / 2) = 2√2.

Na druhej strane, komponent na osi x vektora A sa rovná

Môže vám slúžiť: zložená sukcesia

cos (45 °) = vx / 4, a teda Vx = 4*(√2 / 2) = 2√2.

Odkazy

1. Landaverde, f. D. (1997). Geometria (Opakovanie Ed.). Pokrok.
2. Leake, D. (2006). Trojuholníky (Ilustrované ed.). Heinemann-Raintree.
3. Pérez, C. D. (2006). Predbežné vyfarbenie. Pearson Vzdelanie.
4. Ruiz, Á., & Barrantes, h. (2006). Geometria. CR technologický.
5. Sullivan, m. (1997). Predbežné vyfarbenie. Pearson Vzdelanie.
6. Sullivan, m. (1997). Trigonometria a analytická geometria. Pearson Vzdelanie.