Ako získať uhol trojuholníka? (Príklad)

Existujú rôzne spôsoby Vypočítajte strany a uhly trojuholníka. Závisia od typu trojuholníka, s ktorým pracujete.

Pri tejto príležitosti sa ukáže, ako vypočítať strany a uhly pravého trojuholníka za predpokladu, že určité údaje o trojuholníku so známymi so známymi.

Prvky, ktoré sa použijú, sú:

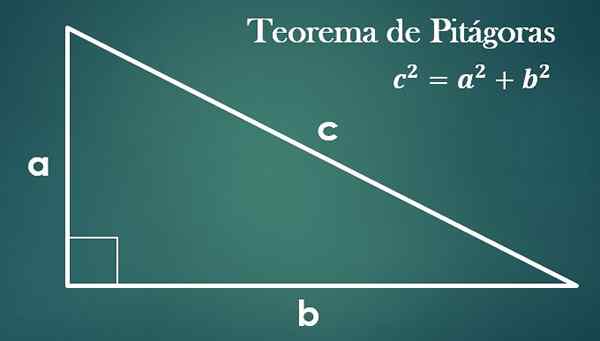
- Pythagorová veta

Vzhľadom na trojuholník obdĺžnika s „A“, „B“ a hypotenusa „C“ je pravda, že „C² = A²+B²“.

- Plocha trojuholníka

Vzorec na výpočet plochy akéhokoľvek trojuholníka je a = (b × h)/2, kde „b“ je dĺžka základne a „h“ dĺžka výšky.

- Uhly trojuholníka

Súčet troch vnútorných uhlov trojuholníka je 180 °.

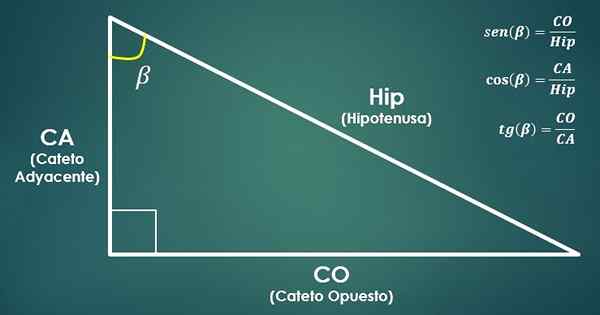
- Trigonometrické funkcie:

Zvážte pravý trojuholník. Potom sú trigonometrické funkcie definované sínus, kosínus a dotyčnica uhol beta (β) nasledovne:

SIN (β) = CO/HYP, COS (β) = Ca/bedra a Tan (β) = CO/Ca.

Ako vypočítať strany a uhly pravého trojuholníka?

Vzhľadom na trojuholník ABC obdĺžnika je možné prezentovať nasledujúce situácie:

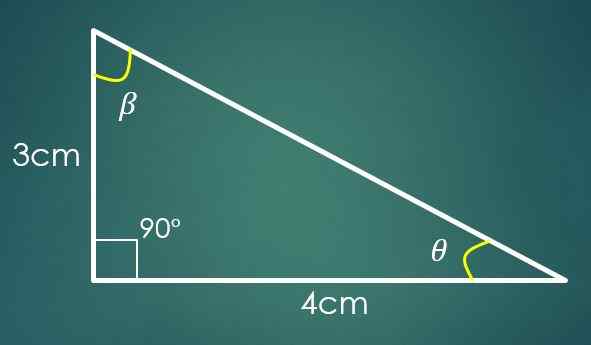
1- Dve nohy sú známe

Ak Cateto „A“ meria 3 cm a Cateto „B“ meria 4 cm, potom sa používa hodnota „C“ veta Pythagorov. Nahradením hodnôt „A“ a „B“ sa získa, že C² = 25 cm², čo znamená, že C = 5 cm.

Teraz, ak je uhol β v rozpore s kategóriou „B“, potom sin (β) = 4/5. Pri aplikácii spätnej funkcie prsníka v tejto poslednej rovnosti sa získa, že β = 53,13 °. Už sú známe dva vnútorné uhly trojuholníka.

Nech 9 je uhol, ktorý zostáva známy, potom 90 °+53,13 °+9 = 180 °, kde sa získa, že 9 = 36,87 °.

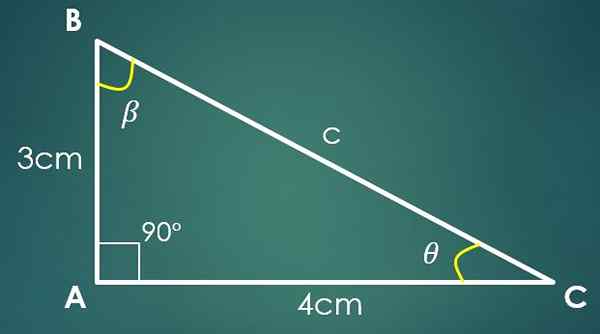
V tomto prípade nie je potrebné, aby boli známe strany dve nohy, dôležité je poznať hodnotu všetkých dvoch strán.

2- noha a oblasť je známa

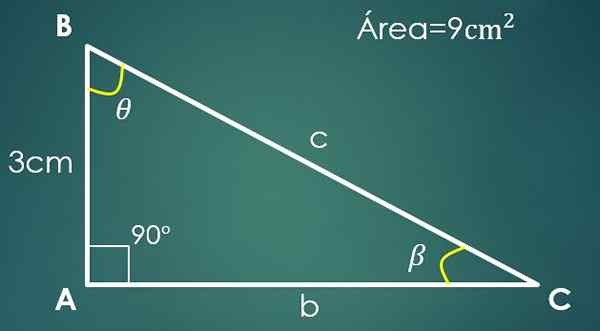
Nech a = 3 cm Známa noha a 9 cm² oblasti trojuholníka.

V obdĺžnikovom trojuholníku sa kategória môže považovať za základnú a druhú ako výšku (pretože sú kolmo).

Predpokladajme, že „A“ je základňa, preto 9 = (3 × h)/2, kde sa získa, že druhá kategória meria 6 cm. Na výpočet hypotenusu postupujte ako v predchádzajúcom prípade a získa sa, že C = √45 cm.

Teraz, ak je uhol β opačný ako kateto „A“, potom sin (β) = 3/√45. Pri čistení β sa získa, že jeho hodnota je 26,57 °. Potrebujete len poznať hodnotu tretieho uhla θ.

Je splnené, že 90 °+26,57 °+9 = 180 °, kde sa dospelo k záveru, že 9 = 63,43 °.

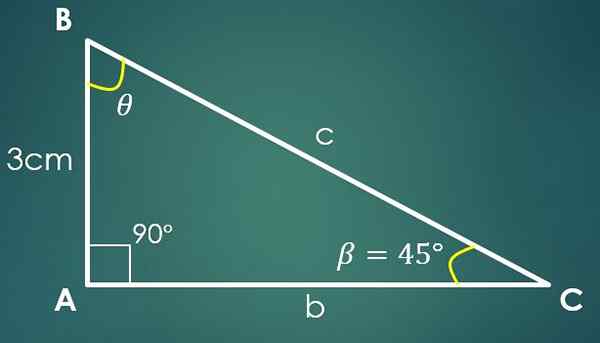
3- Známy je uhol a kateto

Nech β = 45 ° Známy uhol a a = 3 cm známej nohy, kde kateto „a“ je proti uhlu β. Pomocou tangentového vzorca sa získa, že TG (45 °) = 3/Ca, kde sa ukáže, že Ca = 3 cm.

Pomocou vety Pythagora sa získa, že C² = 18 cm², tj C = 3√2 cm.

Je známe, že uhol meria 90 ° a že β meria 45 °, odtiaľ sa dospelo k záveru, že tretí uhol meria 45 °.

V tomto prípade známa strana nemusí byť noha, môže to byť žiadna z troch strán trojuholníka.