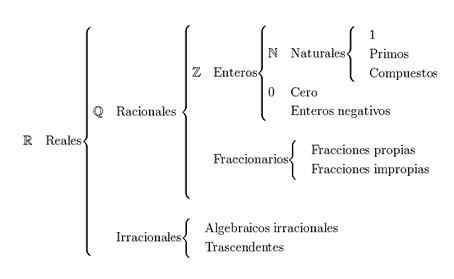
Klasifikácia skutočných čísel

Hlavný Klasifikácia skutočných čísel Je rozdelený na prírodné čísla, celé čísla, racionálne čísla a iracionálne čísla. Skutočné čísla sú zastúpené písmenom R.

Reálne čísla sa vzťahujú na kombináciu racionálnych a iracionálnych čísel skupín. Na vytvorenie týchto skupín sú potrebné prírodné čísla a celé čísla.

Existuje mnoho spôsobov, ako je možné vybudovať alebo opísať rôzne reálne čísla, ktoré sa líšia od jednoduchších foriem po zložitejšie formy, v závislosti od matematickej práce, ktorú chcete vykonať.

Ako sú klasifikované reálne čísla?

- Prirodzené čísla

Prírodné čísla sú reprezentované písmenom (n) a sú čísla používané na počítanie (0,1,2,3,4 ...). Napríklad „existuje pätnásť Rosas v záhrade “,„ Mexiká populácia je z 126 milióny ľudí “alebo„ súčet dva a dva je štvorka„. Je potrebné poznamenať, že niektoré klasifikácie zahŕňajú 0 ako prirodzené číslo a iné nie. 

Dve deti, ktoré robia sumu dvoch prírodných čísel.

Prírodné čísla nezahŕňajú tie, ktoré majú desatinnú časť. Preto „Mexiko populácie pochádza z 126.2 milióny ľudí “alebo„ robí teplotu 24.5 Celsius stupne ”prírodné čísla sa nemohli brať do úvahy.

V spoločnom jazyku, napríklad základných školách, možno prírodné čísla nazvať účtovné čísla, aby sa vylúčili záporné celé čísla a nula.

Prírodné čísla sú základy, s ktorými je možné zostaviť mnoho ďalších sád čísel podľa rozšírenia: celé čísla, racionálne čísla, reálne čísla a zložité čísla, okrem iného.

Vlastnosti prírodných čísel, ako je deliteľnosť a distribúcia primárnych čísel, sa študujú v teórii čísel teórie čísel. Problémy súvisiace s počítaním a objednávaním, ako sú vymeny a oddiel, sa študujú v kombinatorickom.

Majú niekoľko vlastností, ako napríklad: sumu, násobenie, odčítanie, delenie atď.

Môže vám slúžiť: súčasná veda

Čísla

Prírodné čísla môžu byť ordinálne alebo kardinálne.

Kardinálne čísla by boli čísla, ktoré sa používajú ako prírodné čísla, ako je uvedené vyššie v príkladoch. „Mať dva cookies “,„ Som otcom tri deti “,„ Krabica obsahuje dva darčekové krémy “. 

Ordinály sú tie, ktoré vyjadrujú objednávku alebo označujú pozíciu. Napríklad v závode je poradie príchodu bežcov uvedený víťazom a končí posledný, ktorý prišiel na cieľovú čiaru.

Týmto spôsobom sa hovorí, že víťazom je „prvý“, ďalší „druhý“, ďalší „tretí“ a tak ďalej až do posledného. Tieto čísla môžu byť reprezentované písmenom v ich hornej pravici na zjednodušenie písania (1., 2., 3., 4., atď.).

- Celé čísla

Celé čísla sa skladajú z týchto prírodných čísel a ich protikladov, to znamená záporné čísla (0, 1, -1, 2, -2, 50, -50 ...). Rovnako ako prírodné čísla, tieto nezahŕňajú tých, ktorí majú desatinnú časť.

Príkladom celých čísel by bol „priemer 30. v Nemecku“, „Zostal som na 0 po dosiahnutí konca mesiaca“, „Ak chcete ísť dolu do suterénu, musíte označiť tlačidlo výťahu„ výťahu “.

Celé čísla nie je možné napísať s zlomkovou súčasťou. Napríklad čísla ako 8.58 alebo √2 nie sú celé čísla.

Celé čísla sú zastúpené písmenom (z). Z je submailová skupina racionálnych čísel Q, ktorá zase tvorí skupinu skutočných čísel N. Rovnako ako prírodné čísla, Z je nekonečná účtovná skupina.

Celé čísla tvoria najmenšiu skupinu a najmenšiu sadu prírodných čísel. V teórii algebraických čísel sa celé čísla niekedy nazývajú iracionálne, aby ich odlíšili od algebraických celých čísel.

Môže vám slúžiť: výskumný projekt: strany, ako je rozpracovaný a príklad

- Racionálne čísla

Sada racionálnych čísel je reprezentovaná písmenom (q) a obsahuje všetky čísla, ktoré je možné písať ako zlomok celých čísel.

To znamená, že táto sada obsahuje prírodné čísla (4/1), celé čísla (-4/1) a presné desatinné čísla (15,50 = 1550/100).

Distribúcia 1/6 syra je racionálne číslo.

Decimálna expanzia racionálneho čísla sa vždy končí po konečnom počte číslic (napr. 15.50) alebo keď sa začne opakovať rovnaká konečná sekvencia číslic (napr. 0,3456666666666666…). Preto v rámci súboru racionálnych čísel sú čísla zahrnuté. Čisté noviny alebo zmiešané noviny.

Okrem toho akékoľvek opakované alebo terminálne desatinné miesto predstavuje racionálne číslo. Tieto tvrdenia platia nielen pre základňu 10, ale aj pre akékoľvek iné základné číslo.

Skutočné číslo, ktoré nie je racionálne, sa nazýva iracionálne. Iračné čísla zahŕňajú napríklad √2, π a e, napríklad. Pretože celá sada racionálnych čísel je znecitlivená a že skupina reálnych čísel nie je znecitlivená, dá sa povedať, že takmer všetky reálne čísla sú iracionálne.

Racionálne čísla možno formálne definovať ako triedy rovnocennosti celých párov (p, q), takže q ≠ 0 alebo ekvivalentný vzťah definovaný (p1, q1) (p2, q2) iba v prípade p1, q2 = p2q1.

Racionálne čísla, spolu so súčtom a množením, polia formulára, ktoré tvoria celé čísla a sú obsiahnuté v ktorejkoľvek vetve obsahujúcej celé.

- Iracionálne čísla

Iračné čísla sú všetky reálne čísla, ktoré nie sú racionálnymi číslami; Iracionálne čísla nemožno vyjadriť ako zlomky. Racionálne čísla sú čísla zložené z zlomkov celých čísel.

V dôsledku testu speváka, ktorý hovorí, že všetky reálne čísla nie sú neznížiteľné a že racionálne, ak sú čísla, možno dospieť k záveru, že takmer všetky reálne čísla sú iracionálne.

Môže vám slúžiť: trajektóriu a posun

Ak je polomer dvoch čiarových segmentov iracionálne číslo, možno povedať, že tieto segmenty línií sú nezmerateľné; čo znamená, že nie je dostatočná dĺžka, aby každá z nich mohla byť „meranie“ s viacerý.

Medzi iracionálne čísla patrí polomer π kruhového kruhu k jeho priemeru, počet Euler (E), zlaté číslo (φ) a druhá druhá druhá koreň; Ešte viac, všetky odmocniny prírodných čísel sú iracionálne. Jedinou výnimkou z tohto pravidla sú perfektné štvorce.

Je možné poznamenať, že keď sú iracionálne čísla vyjadrené umiestnené v číselnom systéme (napríklad desatinné čísla), nekončia alebo neopakujú.

To znamená, že neobsahujú sekvenciu číslic, opakovanie, ktorým sa vykonáva línia reprezentácie.

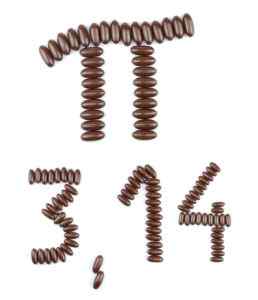Zjednodušenie iracionálneho čísla pi.

Napríklad: desatinné znázornenie čísla π začína 3.14159265358979, ale neexistuje žiadny konečný počet číslic, ktoré môžu presne reprezentovať π, ani sa nemôžu opakovať.

Dôkaz, že desatinné rozšírenie racionálneho čísla sa musí skončiť alebo opakovať, sa líši od dôkazu, že desatinné rozšírenie musí byť racionálne číslo; Aj keď sú základné a trochu dlhé, tieto testy si vyžadujú určitú prácu.

Matematici zvyčajne vo všeobecnosti neberú predstavu „ukončenia alebo opakovania“, aby definovali koncept racionálneho čísla.

Iracionálne čísla sa môžu liečiť aj nekontinuálnymi frakciami.

Odkazy

1. Klasifikuje reálne čísla. Zotavené z Chilimath.com.
2. Prirodzené číslo. Zotavené z Wikipédie.orgán.
3. Klasifikácia čísel. Ditor sa uzdravil.com.
4. Zotavené z Wikipédie.orgán.
5. Iracionálne číslo. Zotavené z Wikipédie.orgán.