Nepružné zrážky v rozmeroch a príkladoch

Ten Nepružné šoky alebo nepružné zrážky sú stručnou a intenzívnou interakciou medzi dvoma objektmi, v ktorých sa zachováva množstvo pohybu, ale nie kinetická energia, z ktorej sa percento transformuje na nejaký iný typ energie.

Otrasy alebo zrážky sú svojou povahou časté. Subatomické častice sa zrážajú pri veľmi vysokých rýchlostiach, zatiaľ čo veľa športov a hier pozostáva z nepretržitých zrážok. Dokonca aj galaxie sú schopné zrážať sa.

postava 1. Skúšobná kolízia. Zdroj: Pixabay

V skutočnosti je množstvo pohybu zachované pri akomkoľvek type kolízie, pokiaľ sa častice zrazia izolovaným systémom. Takže v tomto zmysle nie je problém. Teraz majú objekty kinetickú energiu spojenú s pohybom, ktorý majú. Čo sa môže stať s touto energiou pri havárii?

Vnútorné sily, ktoré sa konajú počas stretu medzi objektmi, sú intenzívne. Keď sa uvádza, že kinetická energia sa nezachováva, znamená to, že sa transformuje na iné typy energie: napríklad v zvukovej energii (kolízia zariadenia má výrazný zvuk).

Viac možností využívania kinetickej energie: teplo trením a samozrejme nevyhnutná deformácia, ktorú utrpeli objekty pri zrážke, ako sú autá telá na obrázku vyššie.

[TOC]

Príklady nepružných kolízií 

- Dve masy plastiínu, ktoré sa zrážajú a stretávajú sa spolu, pohybujú sa ako jeden kus po havárii.

- Gumová guľa, ktorá sa odráža na stenu alebo podlahu. Guľa sa pri náraze na povrch deformuje.

Nie všetka kinetická energia sa transformuje na iné typy energie, s výnimkou niekoľkých výnimiek. Objekty môžu zostať s určitým množstvom tejto energie. Neskôr uvidíme, ako vypočítať percento.

Keď sú kusy, ktoré sa zrážajú, kolízia sa nazýva dokonale nepružná a obidve sa zvyčajne končia spolu s pohybom.

Dokonale nepružné zrážky v rozmere

Zrážka obrázku zobrazuje dva objekty rôznych hmôt m₁ a m₂, Presťahovanie sa k sebe s rýchlosťami vložka_i1 a vložka_I2 respektíve. Všetko sa deje na horizontálnom.

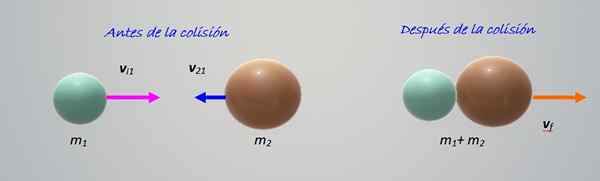Obrázok 2. Zrážka medzi dvoma časticami rôznych hmôt. Zdroj: Self Made.

Objekty sa zrážajú a potom sa zjednotia a pohybujú sa doprava. Je to dokonale nepružná kolízia, takže stačí, aby sme udržali množstvo pohybu:

P_ani = P_F

Množstvo pohybu je vektor, ktorého jednotky sú n.siež. V opísanej situácii je možné vektorové notácie vydávať, pretože ide o zrážky v dimenzii:

Môže vám slúžiť: ľahké experimenty fyziky (primárna univerzita)

Mv_ani = mv_F

Množstvo pohybu systému je vektorový súčet množstva pohybu každej častice.

m₁ vložka_i1  + m₂ vložka_I2 = (m₁ + m₂) v_F

Posledná rýchlosť je daná:

vložka_F = (m₁ vložka_i1  + m₂ vložka_I2)/ (M₁ + m₂)

Reštitúcia

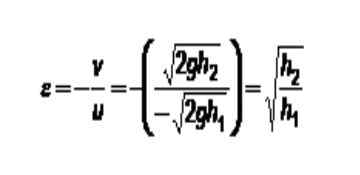
Existuje suma, ktorá môže naznačovať, ako je elastická kolízia. Je to o reštitúcia, ktorý je definovaný ako záporný pomer medzi relatívnou rýchlosťou častíc po havárii a relatívnou rýchlosťou pred haváriou.

Nech u₁ a u₂ Príslušné rýchlosti častíc spočiatku. A buď V₁ a v₂ príslušné konečné rýchlosti. Matematicky je možné koeficient reštitúcie vyjadriť takto:

Koeficient reštitúcie je dodatočná suma, pretože je to pomer medzi rýchlosťami. Poskytnuté informácie sú však veľmi zaujímavé:

- Ak ε = 0 je rovnocenné s tým, že v₂ = v₁. To znamená, že konečné rýchlosti sú rovnaké a stret je nepružná, ako je opísané v predchádzajúcej časti.

- Keď ε = 1 znamená, že relatívne rýchlosti pred a po havárii sa nezmenia, v tomto prípade je stret elastický.

- A ak 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Ako určiť koeficient reštitúcie?

Koeficient reštitúcie závisí od triedy materiálov zapojených do kolízie. Veľmi zaujímavým testom na určenie, ako je elastický materiál na výrobu guličiek, je spadnúť loptu na pevný povrch a zmerať výšku odrazu.

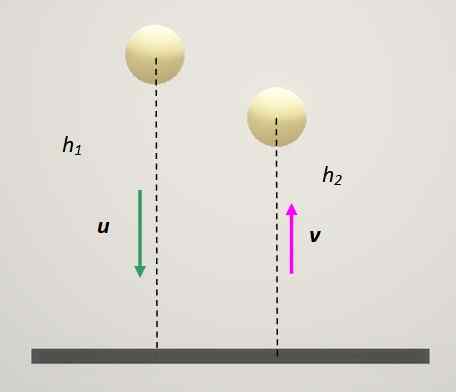Obrázok 3. Metóda na určenie koeficientu reštitúcie. Zdroj: Self Made.

V tomto prípade má pevná doska vždy rýchlosť 0. Ak je k tomu priradený tento index 1 a lopta je: index 2 zostáva:

Počiatočná rýchlosť závisí od výšky h₁ z ktorých spadol:

Záporné znamienko označuje smer dole. A konečná rýchlosť súvisí s maximálnou výškou h₂ To siaha v odrazu:

Nahradenie v koeficiente reštitúcie, ktorý máte:

Výbuchy

Na začiatku bolo navrhnuté, že všetka kinetická energia sa dá transformovať presunom na iné typy energie. Koniec koncov, energia nie je zničená. Je možné, že objekty, ktoré prišli s pohybom, sa zrážajú a spájajú sa a vytvárajú jediný objekt, ktorý je náhle v pokoji? To si nie je také jednoduché predstaviť si.

Môže vám slúžiť: Dynamika: História, aké štúdie, zákony a teórie

Predstavme si však, čo sa stane dozadu, ako vo filme, ktorý je uvedený v chrbte. Potom bol objekt spočiatku odpočinok a potom exploduje fragmentu do niekoľkých častí. Táto situácia je úplne možná: je to výbuch.

Takže výbuch možno považovať za dokonale nepružnú kolíziu, ktorá sa včas dozvedela dozadu. Uchováva sa aj množstvo pohybu, ktorý je schopný potvrdiť:

P_ani = P_F

Vyriešené príklady

-Cvičenie 1

Z meraní je známe, že koeficient reštitúcie ocele je 0.90. Oceľová guľa je spadnutá zo 7 m vysoká na pevnej doske. Vypočítať:

a) Až do akej výšky sa odrazí.

b) ako dlho trvá medzi prvým kontaktom s povrchom a druhým.

Riešenie

a) Rovnica, ktorá bola predtým odvodená v oddiele o určovaní koeficientu reštitúcie, sa používa:

Výška h₂:

0.90² . 7 m = 5.67 m

b) zvýšiť 5.67 metrov rýchlosť daná:

Odkiaľ:

A čas potrebný na dosiahnutie tejto výšky je:

tón _Maximálny = v_ani/ g = (10.54/9.8 s) = 1.08 s.

Čas potrebný na návrat je rovnaký, preto je celkový čas na nahranie 5.67 metrov a návrat do východiskového bodu je dvakrát maximálny čas:

tón_let = 2.15 s.

-Cvičenie 2

Obrázok ukazuje blok dreva s hmotnosťou M visiacim v zvyškoch závitov s dĺžkou L ako kyvadlo. Toto sa nazýva balistické kyvadlo a slúži na meranie rýchlosti V vstupu hmotnosť m. Čím vyššia je rýchlosť, s akou guľka ovplyvňuje blok, vo vyššej výške H sa to postavia.

Obrazová guľka je vložená do bloku, preto je to úplne nepružný šok.

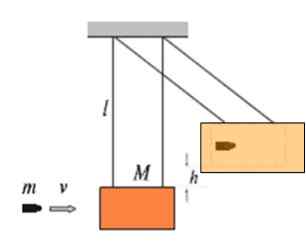Obrázok 4. Balistické kyvadlo.

Predpokladajme, že 9 9.72 g Náraz na hmotnostnom bloku 4.60 kg, potom sada stúpa na 16.8 cm rovnovážnej polohy. Aká je rýchlosť vložka guľka?

Riešenie

Počas kolízie sa zachová množstvo pohybu a alebo_F Je to rýchlosť súboru, keď sa guľka zabuduje do bloku:

P_ani = P_F

Blok spočiatku odpočíva, zatiaľ čo strela je nasmerovaná na cieľ rýchlosťou vložka:

m.v + m.0 = (m + m) u_F

 

Nie je to známe alebo_F Dokonca, ale po zrážke sa zachováva mechanická energia, čo je súčet gravitačnej potenciálnej energie a kinetickej energie K:

Môže vám slúžiť: Súčet vektorov: grafická metóda, príklady, vyriešené cvičenia

Počiatočná mechanická energia = konečná mechanická energia

A_mí = E_Mf

Alebo_ani + Klimatizovať_ani = U_F + Klimatizovať_F

Energia gravitačného potenciálu závisí od výšky, v ktorej sada dosahuje. Pre rovnovážnu polohu je počiatočná výška považovaná za referenčnú úroveň, preto:

Alebo_ani = 0

Vďaka guľke má sada kinetickú energiu Klimatizovať_ani, ktorá sa stáva gravitačným potenciálom energie, keď sada dosiahne svoju maximálnu výšku h. Kinetická energia je daná:

K = ½ mv²

Spočiatku kinetická energia je:

Klimatizovať_ani = (1/2) (m+m) u_F²

Pamätajte, že guľka a blok tvoria jediný masový objekt M+ m. Gravitačná potenciálna energia, keď dosiahli maximálnu výšku, je:

Alebo_F = (m + m) gh

Preto:

Klimatizovať_ani = U_F

(1/2) (m+m) u_F² = (m + m) gh

Teraz je tento výsledok nahradený výrazom vložka ktorý sa vyčistil na začiatku, od zachovania množstva pohybu:

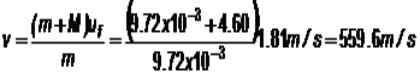
-Cvičenie 3

Predmet obrázku exploduje v troch fragmentoch: dva z rovnakej hmotnosti M a jeden väčší hmotnosť 2 m. Obrázok označuje rýchlosti každého fragmentu po výbuchu. Aký bol počiatočný cieľ objektu?

Obrázok 5. Kameň, ktorý exploduje v 3 fragmentoch. Zdroj: Self Made.

Riešenie

Tento problém si vyžaduje použitie dvoch súradníc: X a a, Pretože dva fragmenty majú vertikálne rýchlosti, zatiaľ čo zostávajúci má horizontálnu rýchlosť.

Celková hmotnosť objektu je súčtom hmotnosti všetkých fragmentov:

M = M + M + 2M = 4 m

Množstvo pohybu je zachované tak na osi X aj na osi y, navrhuje sa osobitne:

1. 4 m. alebo_X= m v₃
2. 4 m. alebo_a = m. 2V₁ - 2 m. vložka₁

Všimnite si, že veľký fragment sa pohybuje nadol s rýchlosťou V1, aby poukázal na túto skutočnosť, že bola umiestnená negatívna značka.

Z druhej rovnice to okamžite nasleduje alebo_a = 0, A prvý je Clear UX okamžite:

Počiatočný cieľ objektu bol u_ani = u_X = v₃/4.

Odkazy

1. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Základy fyziky. Pearson. 135-155.
3. Serway, r., Vulle, C. 2011. Základy fyziky. 9^nat Učenie sa. 172 -182
4. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil. 217-238
5. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. Kopec MacGraw. 185 -195