Elastické otrasy v rozmeroch, špeciálnych prípadoch, cvičeniach

Ten elastické šoky o Elastické zrážky pozostávajú z krátkych, ale intenzívnych interakcií medzi objektmi, v ktorých sa zachovávajú množstvo pohybu a kinetická energia. Choques sú v prírode veľmi časté udalosti: od subatomických častíc po galaxie, prechádzajúce biliardovými guľami a šokovými automobilmi v atrakčných parkoch, všetky sú objekty schopné zrážať sa.

Počas zrážky alebo šoku sú interakčné sily medzi objektmi veľmi intenzívne, oveľa viac ako tie, ktoré môžu konať externe. Týmto spôsobom je možné potvrdiť, že počas zrážky tvoria častice izolovaný systém.

Zrážky medzi biliardovými loptičkami sa môžu považovať za elastické. Zdroj: Pixabay.

V takom prípade je splnené, že:

Kde P Je to vektorové množstvo pohybu, ktorého veľkosť je Mv (Rýchlostná hmota). Ak je derivát P je null, to znamená P Je to konštantné. A to znamená, že sa nemení, že je zachovaný. Preto môžeme potvrdiť:

P_ani = P_F

Množstvo pohybu P_ani Pred kolíziou je rovnaká ako po zrážke. Toto je splnené pre každú zrážku typu, elastické aj nepružné.

Teraz musíte zvážiť nasledujúce: Počas zrážky objekty zažívajú určitú deformáciu. Keď je stret elastický, objekty rýchlo znovu získajú svoju pôvodnú formu.

[TOC]

Ochrana kinetickej energie

Normálne počas šoku sa časť energie objektov vynakladá v horúčave, deformácii, zvuku a niekedy aj pri výrobe svetla. Takže kinetická energia systému po zrážke je menšia ako pôvodná kinetická energia.

Keď kinetická energia k, zachováva sa potom:

Klimatizovať_ani = K_F

Čo znamená, že sily konajúce počas kolízie sú konzervatívne. Zatiaľ čo kolízia trvá, kinetická energia sa krátko zmení na potenciálnu energiu a potom je to opäť kinetická energia. Príslušné kinetické energie sa líšia, ale suma zostáva konštantná.

Dokonale elastické zrážky nie sú časté, hoci biliardové gule sú pomerne dobrý prístup, ako aj zrážky, ktoré sa odohrávajú medzi ideálnymi molekulami plynov.

Elastické šoky v rozmere

Preskúmajme zrážku dvoch častíc v jednej dimenzii; To znamená, že častice, ktoré interagujú, sa pohybujú, povedzme pozdĺž osi x. Predpokladajme, že majú masy m₁ a m₂. Počiatočné rýchlosti každého z nich sú alebo₁ a alebo₂ respektíve. Konečné rýchlosti sú vložka₁ a vložka₂.

Môžeme sa zaoberať bez zápisu vektora, pretože pohyb sa vykonáva pozdĺž osi x, znaky (-) a (+) označujú význam pohybu. Vľavo je negatívny a na pozitívnom pravici, konventom.

Môže vám slúžiť: siete Bravais: Koncept, charakteristiky, príklady, cvičenia

-Vzorce pre elastické zrážky

Pre množstvo pohybu

m₁alebo₁ + m₂alebo₂ = m₁vložka₁ + m₂vložka₂

Pre kinetickú energiu

½ m₁alebo²₁ + ½ m₂alebo²₂ = ½ m₁vložka²₁ +  ½ m₂vložka²₂

Vždy, keď sú známe počiatočné hmoty a rýchlosti, je možné preskupiť rovnice a nájsť konečné rýchlosti.

Problém je v tom, že je v zásade potrebné. Ideálom by bolo nájsť výrazy, ktoré ich neobsahujú.

Prvým je urobiť bez faktora ½ a usporiadať obe rovnice takým spôsobom, že sa objaví negatívny znak a masy môžu byť faktorom:

m₁alebo₁ - m₁vložka₁ = M₂vložka₂ - m₂alebo₂

m₁alebo²₁ - m₁vložka²₁  = +M₂vložka²₂ - m₂alebo²₂

Byť vyjadrený týmto spôsobom:

m₁(alebo₁ - vložka₁ ) = m₂(v₂ - alebo₂)

m₁(alebo²₁ - vložka²₁ ) = m₂ (v²₂ - alebo²₂)

Zjednodušenie na odstránenie štvorcov z rýchlostí

Teraz musíte použiť pozoruhodný produkt, zvyšuje jeho rozdiel v druhej rovnici, ktorá získa výraz, ktorý neobsahuje štvorce, ako sa pôvodne chcelo:

m₁(alebo₁ - vložka₁ ) = m₂(v₂ - alebo₂)

m₁(alebo₁ - vložka₁ ) (alebo₁ + vložka₁ ) = m₂ (v₂ - alebo₂) (v₂ + alebo₂)

Ďalším krokom je nahradenie prvej rovnice v druhej:

m₂(v₂ - alebo₂) (alebo₁ + vložka₁ ) = m₂ (v₂ - alebo₂) (v₂ + alebo₂)

A keď sa tento výraz opakuje m₂(v₂ - alebo₂) Na oboch stranách rovnosti je tento výraz zrušený a je taký:

(alebo₁ + vložka₁) = (V₂ + alebo₂)

Alebo ešte lepšie:

alebo₁ - alebo₂= v₂ -  vložka₁

Konečné rýchlosti v₁ a v₂ častíc

Teraz existujú dve lineárne rovnice, s ktorými je ľahšie pracovať. Znovu ich umiestnime pod druhú:

m₁alebo₁ + m₂alebo₂ = m₁vložka₁ + m₂vložka₂

alebo₁ - alebo₂= v₂ -  vložka₁

Vynásobenie druhej rovnice pomocou m₁ A pridanie termínu do termínu zostáva:

m₁alebo₁ + m₂alebo₂ = m₁vložka₁ + m₂vložka₂

m₁alebo₁ - m₁alebo₂= m₁vložka₂ - m₁ vložka₁

-

2 m₁alebo₁ + (m₂ - m₁) alebo₂ = (m₂ + m₁) v₂

A už je možné vyčistiť vložka₂. Napríklad:

Podobné ošetrenie je možné vykonať na nájdenie rovnice pre vložka₁. Čitateľ je ponechaný ako cvičenie, ktoré preukáže, že:

Osobitné prípady elastických kolízií

Teraz, keď sú rovnice k dispozícii pre konečné rýchlosti oboch častíc, je čas analyzovať niektoré špeciálne situácie.

Dve rovnaké masy

Potom m₁ = m₂ = m a:

vložka₁ = u₂

vložka₂ = u₁

Častice jednoducho vymenia svoje rýchlosti po zrážke.

Dve rovnaké masy, z ktorých jedna bola pôvodne v pokoji

Znova  m₁ = m₂ = m a za predpokladu alebo₁ = 0:

vložka₁ = u₂

vložka₂ = 0

Po havárii sa častica, ktorá bola v pokoji, získava rovnakú rýchlosť častíc, ktorá sa pohybovala, a zase sa zastavuje.

Môže vám slúžiť: hydraulický tlak

Dve rôzne masy, jedna z nich spočiatku v pokoji

V tomto prípade predpokladajme alebo₁ = 0, Ale masy sú rôzne:

Čo ak m₁ je oveľa väčší ako m₂?

Stáva sa to, že m₁ Držte sa v pokoji a m₂ Vracia sa s rovnakou rýchlosťou, s akou ovplyvnila.

Huygens-Newton Restitution Coeficient alebo Pravidlo

Predtým sa odvodil nasledujúci vzťah medzi rýchlosťami pre dva objekty pri elastickej kolízii: alebo₁ - alebo₂ = v₂ -  vložka₁. Tieto rozdiely sú relatívne rýchlosti pred a po zrážke. Všeobecne platí, že na zrážku je splnená, že:

alebo₁ - alebo₂ = -(v₁ -  vložka₂)

Koncept relatívnej rýchlosti je lepšie ocenený, ak si čitateľ predstaví, že je na jednej z častíc a z tejto polohy pozoruje rýchlosť, s ktorou sa pohybuje druhá častice. Predchádzajúca rovnica je prepísaná takto:

Ak kinetická energia nie je zachovaná, potom bude uvedený kvocient menší ako 1. Zavolajme a na hodnotu uvedeného bezrozmerného kvocientu:

O dobre:

Hodnota a je medzi 0 a 1 a nazýva sa reštitúcia. Keď je stret elastický, E = 1. Ak je úplne nepružná, e = 0, zatiaľ čo ak má inú strednú hodnotu, nejaká kinetická energia sa rozptýlila v iných druhoch energie.

Vyriešené cvičenia

-Cvičenie vyriešené 1

Biliardová guľa sa presunie doľava pri 30 cm/s a zráža sa spredu s ďalšou identickou guľou, ktorá sa pohybuje doprava na 20 cm/s. Obidve gule majú rovnaké cesto a havária je dokonale elastická. Nájdite rýchlosť každej lopty po náraze.

Riešenie

alebo₁ = -30 cm/s

alebo₂ = +20 cm/s

Toto je osobitný prípad, že v elasticky dimenzii sa zrážajú dve rovnaké masy, a preto sa vymenia rýchlosť.

vložka₁ = +20 cm/s

vložka₂ = -30 cm/s

-Cvičenie vyriešené 2

Restitučný koeficient lopty, ktorá sa odráža na zemi, sa rovná 0,82. Ak spadnete z odpočinku, aký zlomok vašej pôvodnej výšky sa dostane po loptičke po odrazení raz? A po 3 doskokoch?

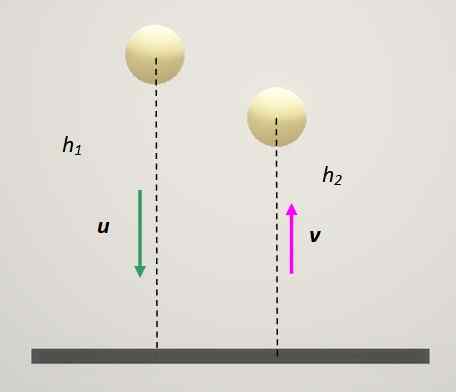Guľa sa odráža proti pevnému povrchu a pri každom odskočení stráca výšku. Zdroj: Self Made.

Riešenie

Pôda môže byť objektom 1 v reštitučnej koeficientnej rovnici. A vždy je to v pokoji, takže:

Negatívny smer je vybraný dole a pozitívny. Rýchlosť objektu, ktorý je voľne uvoľnený z určitej výšky h_ani je:

Znak (-) označuje, že lopta zostupuje:

Môže vám slúžiť: Torricelli Experiment: Opatrenia atmosférického tlaku, dôležitosť

 

S touto rýchlosťou skákaním:

 

Značka + označuje, že ide o stúpajúcu rýchlosť. A podľa nej lopta dosahuje maximálnu výšku:

 

Teraz sa opäť vracia na zem s rýchlosťou rovnakej veľkosti, ale opačným znakom:

A odrazí sa s:

To dosahuje maximálnu výšku:

Znova sa dostanete na zem s:

Následné doskoky

Zakaždým, keď sa lopta odrazí a vystúpi, musíte znova vynásobiť rýchlosť 0.82:

A dosahuje maximálnu výšku určenú štvorcom uvedenej rýchlosti:

V tomto bode h₃ je približne 30% h_ani. Aká by bola výška na 6. doskokoch bez toho, aby musela robiť výpočty tak podrobné ako tie predchádzajúce?

bol by som h₆ = 0.82¹² h_ani = 0.092h_ani alebo iba 9% h_ani.

-Cvičenie vyriešené 3

Blok 300 g sa pohybuje na sever k 50 cm/s a zráža sa proti 200 g bloku, ktorý je nasmerovaný na juh 100 cm/s. Predpokladajme, že stret je dokonale elastický. Nájdite rýchlosti po náraze.

Údaje

m₁ = 300 g; alebo₁ = + 50 cm/s

m₂ = 200 g; alebo₂ = -100 cm/s

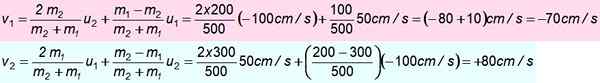
-Cvičenie vyriešené 4

Vydáva sa množstvo M₁ = 4 kg od bodu uvedeného na trati bez trenia, až kým sa nezráža s m₂ = 10 kg v pokoji. Do akej výšky je m₁ Po zrážke?

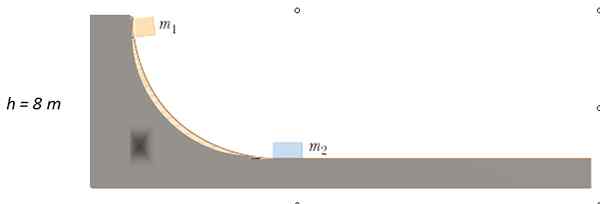
Riešenie

Pretože nedochádza k treniu, zachováva sa mechanická energia na nájdenie rýchlosti alebo₁ s čím m₁ vplyvy  m_2. Spočiatku kinetická energia je 0, odvtedy m₁ časť zvyšku. Pri pohybe na vodorovnom povrchu nemá výšku, takže potenciálna energia je 0.

Mgh = ½ mu₁ ²

 

alebo₂ = 0

Teraz rýchlosť m₁ Po zrážke:

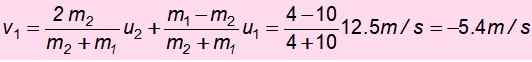
Negatívny znak znamená, že bol vrátený. S touto rýchlosťou stúpa a mechanická energia sa znova zachováva, aby sa našlo Hm, Výška, v ktorej sa mu podarí vystúpiť po havárii:

½ MV₁² = mgh '

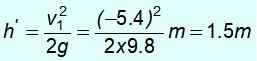
Všimnite si, že sa nevrátite do východiskového bodu vo výške 8 m. Nemá dostatok energie, pretože dala časť svojej kinetickej energie hmotnosť m_1.

Odkazy

1. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Základy fyziky. Pearson. 135-155.
3. Serway, r., Vulle, C. 2011. Základy fyziky. 9^nat Učenie sa. 172 -182
4. Tipler, P. (2006) Fyzika pre vedu a techniku. 5. vydanie. Zväzok 1. Redaktor sa vrátil. 217-238
5. Tippens, P. 2011. Fyzika: Koncepty a aplikácie. 7. vydanie. Kopec MacGraw. 185 -195