Stred gravitačných vlastností, výpočet, príklady

On gravitačný centrum telesného telesa merateľnej veľkosti je bod, v ktorom sa jeho hmotnosť považuje za aplikovanú. Je preto jedným z hlavných konceptov statického.

Prvým prístupom v problémoch so základnou fyzikou je predpokladať, že akýkoľvek objekt sa správa ako špecifická hmota, to znamená, že mu chýba rozmery a celá hmota sa koncentruje v jednom bode. Toto platí pre krabicu, auto, planétu alebo subatomickú častice. Tento model je známy ako časticový model.

postava 1. Vo výške ich športovec opravuje tak, aby jeho ťažisko bolo mimo tela. Zdroj: Pixabay

Prirodzene je to prístup, ktorý poskytuje veľmi dobré výsledky pre mnoho aplikácií. Nie je ľahké zvážiť individuálne správanie tisícov a miliónov častíc, ktoré by mohol obsahovať akýkoľvek objekt.

Skutočné rozmery vecí by sa však mali zohľadniť, ak chcete. Pretože sme zvyčajne v bezprostrednej blízkosti Zeme, vždy súčasná sila na ktoromkoľvek tele je presne váha.

[TOC]

Úvahy o nájdení ťažiska 

Ak sa vezme do úvahy veľkosť tela? Ak máte svojvoľne nepretržitý objekt, jeho hmotnosť je a Distribuovaná sila medzi každou z jeho zložkových častíc.

Nech tieto častice m₁, m₂, m₃... Každá z nich zažíva svoju zodpovedajúcu gravitačnú silu m₁g, m₂g, m₃G ..., všetky paralelné. Je to tak, pretože gravitačné pole Zeme sa vo veľkej väčšine prípadov považuje za konštantné, vzhľadom na skutočnosť, že objekty sú malé v porovnaní s veľkosťou planéty a sú blízko jej povrchu.

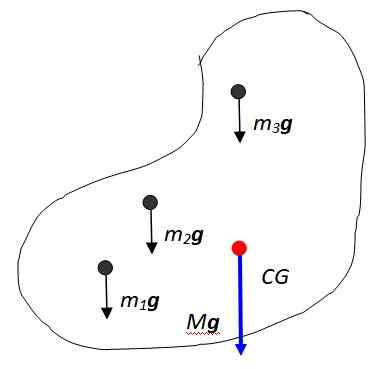Obrázok 2. Hmotnosť objektu je distribuovaná hmota. Zdroj: Self Made.

Vektorový súčet týchto síl vedie k hmotnosti objektu, aplikovaného na bod nazývaný ťažisko označený na obrázku ako CG, čo sa potom zhoduje s Hromadné centrum. Hromadné centrum je zase bodom, v ktorom by sa celá hmotnosť mohla považovať za koncentrovanú.

Výsledná hmotnosť má veľkosť Mg kde M Je to celková hmotnosť objektu a samozrejme je nasmerovaná vertikálne smerom do stredu Zeme. Sumory notácia je užitočná na vyjadrenie celkového tela tela:

Symetrické a homogénne objekty, ktoré sú rovnocenné s rovnomernou hustotou, majú ťažisko v geometrickom centre: kocky, paralepipeds, krúžky, pneumatiky alebo gule.

Stred gravitácie nie vždy zodpovedá materiálnemu bodu. Napríklad CG obruče je vo svojom geometrickom centre, kde nie je samotné cesto. Napriek tomu, ak chcete analyzovať sily, ktoré pôsobia na obruč, musí sa na tento presný bod aplikovať hmotnosť.

V akých prípadoch, v ktorých je objekt svojvoľný, ak je homogénny, jeho hmotnostné centrum je možné stále vypočítať nájdením stredobod o Baricentro obrázku.

Môže vám slúžiť: ortuť (planéta)

Ako sa vypočíta ťažisko?

V zásade, ak sa stredisko gravitácie (CG) a hmotnostné centrum (CM) zhodujú, keď je gravitačné pole rovnomerné, potom sa môže vypočítať cm a na ňu nanášajú hmotnosť.

Zvážte dva prípady: prvý je ten, v ktorom je distribúcia hmotnosti diskrétne; to znamená, že môžete spočítať každú hmotnosť, ktorá tvorí systém a priraďuje číslo I, ako sa to stalo v predchádzajúcom príklade.

Súradnice centra hmotnosti pre diskrétnu hmotnostnú distribúciu sú: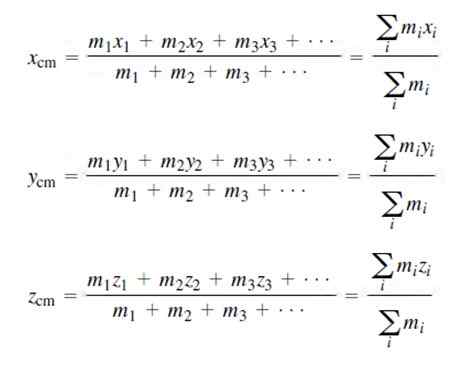

Samozrejme, súčet všetkých hmôt je ekvivalentný celkovej hmotnosti systému M, ako je uvedené vyššie.

Pri posudzovaní vektora r sa tieto tri rovnice redukujú na kompaktný tvar_cm o Vektor polohy hmotnostného centra:

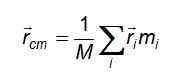
A v prípade kontinuálneho rozloženia hmotnosti, kde sú častice s diferenciálnou veľkosťou a nemožno ich rozlíšiť, aby ich spočítali, je suma nahradená integrálom, ktorý sa vytvára o objeme obsadenom predmetom predmetu:

Kde r Je to polohový vektor diferenciálnej hmoty Dm A definícia hmotnostnej hustoty na vyjadrenie hmotnostného diferenciálu sa uskutočnila Dm obsiahnuté v objemovom diferenciáli DV:

Hustota objektu môže byť konštantná, v takom prípade vychádza z integrálu alebo je funkciou priestorových súradníc a musíme poznať jeho závislosť od (x, y, z) na vyriešenie integrálu.

Vlastnosti

Niektoré dôležité úvahy o hmotnostnom centre sú nasledujúce:

- Aj keď je na vytvorenie pozícií vyžadovaný referenčný systém, centrum hmotnosti nezávisí od výberu systému, pretože ide o vlastnosť objektu.

- Ak má objekt osi alebo rovinu symetrie, hmotnostné stredisko je na uvedenej osi alebo rovine. Využite výhody tejto okolnosti šetrí čas výpočtu.

- Všetky vonkajšie sily pôsobiace na objekt sa môžu aplikovať na hmotnostné centrum. Po sledovaní tohto bodu poskytuje globálnu predstavu o pohybe objektu a uľahčuje prácu pri štúdiu jeho správania.

-Nájdenie ťažiska tela v statickej rovnováhe

Predpokladajme, že telo predchádzajúceho čísla je v statickej rovnováhe.

Obrázok 3. Schéma na výpočet krútiaceho momentu hmotnosti vzhľadom na bod alebo.

Moment sieti o torzii vzhľadom na O, podľa obrázku 3 je: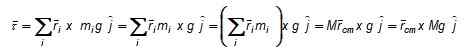Sila F aplikovaná vertikálne hore v strede gravitácie (alebo tiež nad alebo pod, na osi, ktorá cez ňu prechádza) by vytvorila opačné krútenie, ktoré by zabránilo rotácii objektu a zachovalo by sa rotačná rovnováha. Rozsah f sa vyberie tak, aby sa objekt nepreniesol, a týmto spôsobom ho budeme mať v statickej rovnováhe.

Môže vám slúžiť: zvlnená optika

-Vyriešený príklad

Tenká tyčinka rovnomerného materiálu má dĺžku 6 metrov a váži 30 N. Na konci je obesený 50 N na západ a ďalší z 20 N na pravom konci. Nájdite: a) rozsah stúpajúcej sily potrebnej na udržanie rovnováhy tyče, b) stredný gravitačný súbor.

Riešenie

Schéma síl je znázornená na nasledujúcom obrázku. Hmotnosť tyče sa aplikuje v ťažiskom gravitácii, ktorá sa zhoduje s geometrickým centrom. Jedinou dimenziou zohľadnenej tyče je jej dĺžka, pretože vyhlásenie informuje, že je tenký.

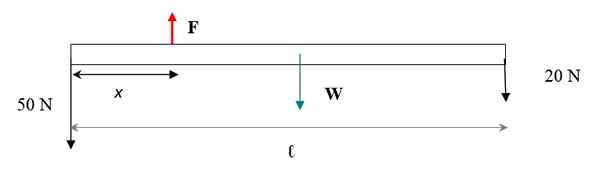Obrázok 4. Diagram Pàra la Barra.

Aby systém typu + hmotnosť zostal v prekladovej rovnováhe, súčet síl musí byť nulová. Sily sú vertikálne, ak zvážime znak + a dole so znakom - potom:

F-50- 20-30 n = 0

F = 100 n

Táto sila zaručuje rovnováhu prekladu. Berúc na chvíľu torzie všetkých síl týkajúcich sa osi, ktorá prechádza ľavým koncom systému, a uplatňovaním definície:

t = r x f

Momenty všetkých týchto síl vzhľadom na vybraný bod sú kolmé na rovinu baru:

tón_F = xf = 100x

tón_W = -(l/2) mg = -3m . 30 n = -90 n.m

tón₁ = 0 (pretože sila 50 N prechádza zvolenou osou a nekonáva moment)

tón₂ = -Lf₂ = 6 m . 20 n = -120 n.m

Preto:

100 x -90 -120 N.m = 0

x = 2.10 m

Stred gravitácie barovej tyče + hmotnosti sa nachádza na 2.10 metrov z ľavého konca baru.

Rozdiel v centre hmotnosti

Stred gravitácie sa zhoduje so stredom hmotnosti, ako je uvedené, pokiaľ je pozemné gravitačné pole konštantné pre všetky body objektu. Gravitačné pole Zeme nie je nič iné ako dobre známa a známa hodnota G = 9.8 m/s² nasmerované vertikálne nadol.

Aj keď hodnota G zažíva variácie so zemepisnou šírkou a nadmorskou výškou, zvyčajne neovplyvňujú objekty, o ktorých sa väčšinou zaobchádza. Veľmi odlišné by bolo, keby sa považovalo za veľké telo v blízkosti Zeme, napríklad asteroid, ktorý by sa blížil k planéte.

Asteroid má svoje vlastné masové centrum, ale jeho ťažisko by sa s tým už nemuselo časovo zhodovať, odvtedy g Pravdepodobne by to zaznamenalo značné rozdiely v veľkosti, vzhľadom na veľkosť asteroidu a že hmotnosti každej častice nemusia byť rovnobežné.

Ďalším základným rozdielom je to, že centrom hmoty je bez ohľadu na to, či existuje alebo nie je sila nazývaná použitá hmotnosť na objekt. Je to vnútorná vlastnosť objektu, ktorá odhaľuje, ako je jeho hmota distribuovaná vo vzťahu k jeho geometriu.

Môže vám slúžiť: Aká je dielektrická konštanta?

Hromadné centrum existuje oboje, ak sa použije hmotnosť, akoby nie. A je umiestnený v rovnakej polohe, aj keď sa objekt prenáša na inú planétu, v ktorej je gravitačné pole iné.

Na druhej strane, ťažisko je jasne spojené s uplatňovaním hmotnosti, pretože sme boli schopní oceniť v predchádzajúcich odsekoch.

Príklady gravitácie

Ťažisko nepravidelných objektov

Je veľmi ľahké zistiť, kde je ťažisko nepravidelného objektu ako pohár. Najprv je zavesený z ktoréhokoľvek bodu a odtiaľ je nakreslená vertikálna čiara (na obrázku 5 je to línia Fuchsia v ľavom obrázku).

Potom je zavesený z iného bodu a je nakreslená nová vertikálna (tyrkysová čiara na správnom obrázku). Križovatka oboch línií je stredobodom gravitácie pohára.

Obrázok 5 . CG Umiestnenie šálky. Zdroj: Upravené pixabay.

Rovnováha objektov

Analyzme stabilitu nákladného vozidla, ktorý cirkuluje pozdĺž cesty. Keď je ťažisko nad základňou nákladného vozidla, nebude sa nalievať. Obrázok vľavo je najstabilnejšou polohou.

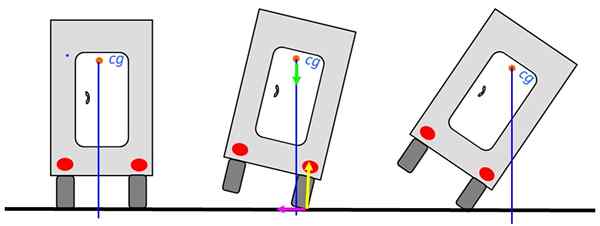Obrázok 6. Vyváženie nákladného vozidla. Zdroj: Self Made.

Aj keď sa kamión nakloní doprava, môže sa vrátiť do stabilnej rovnovážnej polohy, rovnako ako pri výkrese média, pretože vertikál stále prechádza základňou. Keď však táto linka prechádza mimo nákladného vozidla, otočí sa.

Schéma ukazuje sily v podpornom bode: normálna žltá, hmotnosť zelenej a statické trenie vľavo vo Fuchsii. Normálny a rubb. Preto neprispievajú k vyhodeniu nákladného vozidla.

Zostáva hmotnosť, ktorá cvičí okamih torzie, našťastie v anti -horskom zmysle a ktorá má tendenciu sa vrátiť do nákladného vozidla do svojej rovnovážnej polohy. Všimnite si, že vertikálna čiara prechádza podporným povrchom, ktorým je pneumatika.

Keď je kamión v polohe extrémnej pravice, čas krútenia hmotnosti sa zmení a stáva sa v napätom smere. Ak nebudete môcť pôsobiť inokedy, kamión nalieva.

Odkazy

1. Bauer, w. 2011. Fyzika pre inžinierstvo a vedy. Zväzok 1. MC Graw Hill.  247-253.
2. Giancoli, D.  2006. Fyzika: Princípy s aplikáciami. 6. ... Ed Prentice Hall. 229-238.
3. Resnick, r. (1999). Fyzický. Zvuk. 1. 3. vydanie. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 331-341.
4. Rex, a. 2011. Základy fyziky. Pearson.146-155.
5. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1.340-346.