Miera oblúka (geometria), typy oblúkov, príklady

On klonovať sa, V geometrii je to akákoľvek zakrivená čiara, ktorá spája dva body. Zakrivená čiara, na rozdiel od priamky, je to, že koho smer sa v každom bode líši. Opak oblúka je segment, pretože ide o priamu sekciu, ktorá sa spája s dvoma bodmi.

Oblúk, ktorý sa najčastejšie používa v geometrii, je obvod obvodu. Ďalšími oblúkmi bežného použitia sú parabolický oblúk, eliptický oblúk a Cotenary Arch. Forma oblúka sa často používa aj v architektúre ako dekoratívny prvok a konštrukčný prvok. Toto je prípad prekladov dverí a okien, ako aj mostov a akvaduktov.

postava 1. Dúha je zakrivená čiara, ktorá spája dva body na obzore. Zdroj: Pixabay

[TOC]

Oblúk a jeho miera

Miera oblúka je jeho dĺžka, ktorá závisí od typu krivky, ktorá spája dva body a ich umiestnenie.

Dĺžka kruhového oblúka je jednou z najjednoduchších na výpočet, pretože je známa celá dĺžka oblúka alebo obvod kruhu.

Obvod kruhu je dva pI krát vaše rádio: P = 2 π r. Ak to viete, ak chcete vypočítať dĺžku siež kruhového oblúka uhla α (merané v Radiane) a rádiu R, Použije sa podiel:

(s / p) = (a / 2 π)

Potom vyčistenie siež predchádzajúceho výrazu a nahradenie obvodu p jeho výrazom v závislosti od rádiu R, Máš:

S = (a / 2 π) p = (a / 2 π) (2 π r) = a r.

To znamená, že miera kruhového oblúka je produktom jeho uhlového otvoru polomerom kruhového oblúka.

Pre oblúk všeobecne je problém komplikovanejší, do tej miery, že veľkí myslitelia staroveku tvrdili, že to bola nemožná úloha.

Môže vám slúžiť: Aké sú algebraické výrazy a ktoré sú najčastejšie?

Problém merania akéhokoľvek oblúka sa uspokojivo vyriešil, až do príchodu diferenciálneho a integrálneho počtu v roku 1665 sa uspokojivo vyriešilo. 

Pred vynálezom diferenciálneho počtu sa dali nájsť iba roztoky pomocou oblúkov polygonálnej čiary alebo obvodu, ktoré sa blížili k skutočnému oblúku, ale tieto roztoky neboli presné. 

Typy oblúkov

Z hľadiska geometrie sú oblúky klasifikované podľa zakrivenej čiary, ktorá sa spája s dvoma bodmi lietadla. Existujú aj ďalšie klasifikácie podľa jeho architektonického použitia a formy.

Kruhový oblúk

Keď čiara, ktorá spája dva body roviny, je kus obvodu určitého polomeru, existuje kruhový oblúk. Obrázok 2 zobrazuje kruhový oblúk polomeru R, ktorý spája body A a B.

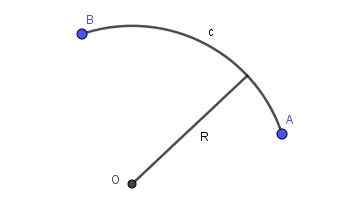Obrázok 2. Rádio r kruhový oblúk, ktorý spája bod A a B. Pripravil Ricardo Pérez.

Parabolický oblúk

Podobenstvo je trajektória, ktorá sleduje objekt, ktorý bol hodený do vzduchu v šikmej podobe. Keď je krivka, ktorá spája dva body.

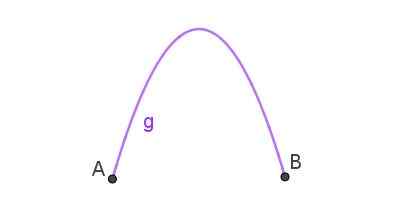Obrázok 3. Parabolický oblúk, ktorý spája body A a B. Pripravil Ricardo Pérez.

Toto je tvar, ktorý prijíma vodný prúd, ktorý vychádza z hadice, ktorá poukazuje nahor. Parabolický oblúk je možné pozorovať vo vodných zdrojoch.

Obrázok 4. Parabolický oblúk tvorený vodou zo zdroja v Drážďanoch. Zdroj: Pixabay.

Oblúk

Oblúk Cotenary je ďalší prírodný oblúk. Cotenár je krivka, ktorá sa prirodzene vytvára, keď reťaz alebo lano pohodlne visí z dvoch samostatných bodov.

Môže vám slúžiť: Aké sú prvky uhla?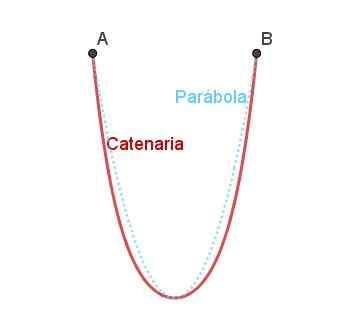 Obrázok 5. Oblúk a porovnanie s parabolickým oblúkom. Pripravil Ricardo Pérez.

Cotenár je podobný parabole, ale nie je to úplne rovnaké, ako je možné poznamenať na obrázku 4.

Invertovaný oblúk v tvare trusu sa používa v architektúre ako štrukturálny prvok s vysokým kompresným odporom. V skutočnosti je možné preukázať, že je to najodolnejší typ oblúka medzi všetkými možnými formami. 

Na vybudovanie tuhého oblúka trotáru sa skopíruje iba tvar lana alebo reťaz.

Eliptický oblúk

Oblúk je eliptický, ak krivka, ktorá spája dva body, je úsek alebo úsek elipsy. Elipsa je definovaná ako geometrické miesto bodov, ktorých vzdialenosť k dvom bodom vždy dodáva konštantné množstvo.

Elipsa je krivka, ktorá sa objavuje v prírode: je to krivka trajektórie planéty okolo slnka, ako demonštroval Johannes Kepler v roku 1609.

V praxi môže byť elipsa nakreslená umiestnením dvoch vzperov na podlahu alebo dvoch kolíkov na papier a zviazaním lana k nim. Potom je lano napäté so značkou alebo ceruzkou a krivka sa nakreslí. Kúsok elipsy je eliptický oblúk. Nasledujúca animácia ilustruje, ako sa nakreslí elipsa:

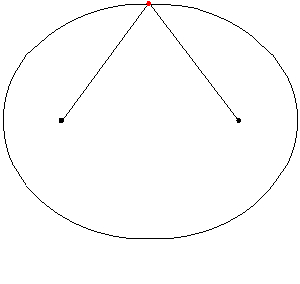Obrázok 5. Posen elipsy pomocou napätého lana. Zdroj: Wikimedia Commons

Obrázok 6 zobrazuje eliptický oblúk, ktorý spája body G a H.

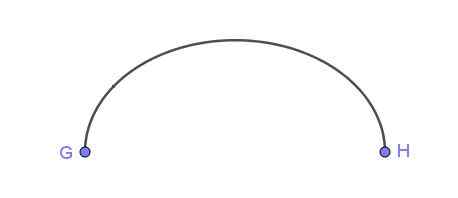Obrázok 6. Eliptický oblúk, ktorý spája dva body. Pripravil Ricardo Pérez.

Príklady oblúkov

Nasledujúce príklady sa vzťahujú na to, ako vypočítať obvod niektorých konkrétnych oblúkov.

Môže vám slúžiť: Transcendentné čísla: čo sú, vzorce, príklady, cvičenia

Príklad 1

Obrázok 7 zobrazuje okno končené v rezanom kruhovom oblúku. Rozmery znázornené na obrázku sú na nohách. Vypočítajte dĺžku oblúka.

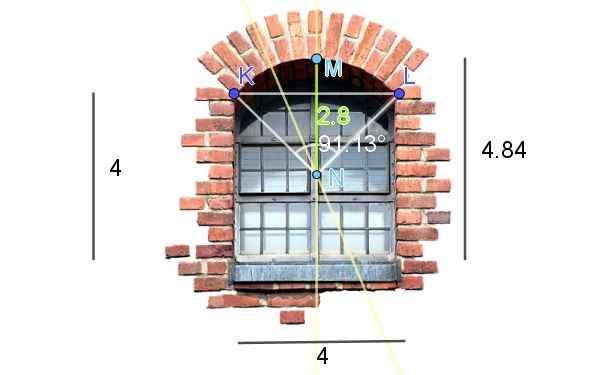Obrázok 7. Výpočet dĺžky kruhového oblúka okna. (Vlastné anotácie - obrázok okna v Pixabay)

Ak chcete získať stred a polomer kruhového oblúka prekladu okna, na obrázku sa vytvoria nasledujúce konštrukcie:

-Je nakreslený segment KL a je nakreslená jeho mediacia.

-Potom sa nachádza najvyšší bod prekladu, ktorý voláme m. Potom sa uvažuje o segmente KM a je nakreslená jeho mediacia.

Odpočúvanie týchto dvoch mediácií je bod n a je tiež stredom kruhového oblúka.

-Teraz musíte zmerať dĺžku segmentu NM, ktorý sa zhoduje s polomerom R kruhového oblúka: r = 2.8 stôp.

-Poznať dĺžku oblúka okrem polomeru, uhol, ktorý tvorí oblúk. Ktoré môžu byť určené dvoma metódami alebo sa merajú pomocou transportéra alebo sa striedavo vypočítajú pomocou trigonometrie.

V prípade, že uhol, ktorý tvorí oblúk, je 91,13 °, ktorý sa musí previesť na radiány:

 91,13 ° = 91,13 ° * π / 180 ° = 1,59 radiánov

Nakoniec vypočítame dĺžku siež oblúka cez vzorec S = α R.

S = 1,59 * 2.8 stôp = 4,45 stôp

Príklad 2

Nájdite dĺžku eliptického oblúka znázornené na obrázku 8, známy r a menšia semifinácia siež elipsa.

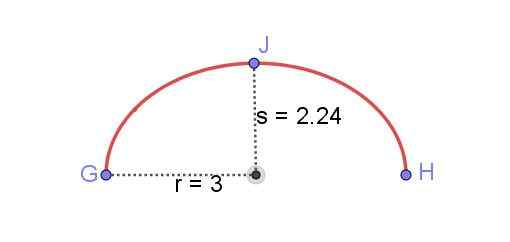Obrázok 8. Eliptický oblúk medzi GH. Pripravil Ricardo Pérez.

Nájdenie dĺžky elipsy bolo po dlhú dobu jedným z najťažších problémov matematiky. Riešenia vyjadrené eliptickými integrmi je možné získať, ale aby sa mali numerická hodnota, tieto integrály v výkone sa musia rozšíriť. Presný výsledok by si vyžadoval nekonečné podmienky týchto sérií.

Našťastie matematický génius hinduistického pôvodu Ramanujan, ktorý žil v rokoch 1887 až 1920, našiel vzorec, ktorý sa veľmi presne približuje obvodu elipsy:

Obvod elipsy = π [3 (r + s) - √ ((3r + s) (r + 3s))]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]]

Obvod elipsy s r = 3 cm a s = 2.24 cm je 16,55 cm. Zobrazený eliptický oblúk má však polovicu tejto hodnoty:

Eliptická oblúková dĺžka GH = 8.28 cm.

Odkazy

1. Clemens. 2008. Geometria a trigonometria. Pearson Vzdelanie.
2. Garcia f. Numerické postupy v Jave. Dĺžka elipsy. Zdroj: SC.Ehu.je
3. Dynamická geometria. Oblúky. Zotavené z Geometriadinamica.je
4. Pištoľ. Elipsy a podobenstvá okolo nás. Zdroj: Pigedas.com
5. Wikipedia. Oblúk (geometria). Obnovené z: Je to.Wikipedia.com