Definícia faktora, vzorce a cvičenia

On Faktorová súprava Je to jednoduchý stroj, ktorý pozostáva z usporiadania kladky s multiplikačným efektom sily. Týmto spôsobom môžete zvýšiť zaťaženie, ktoré aplikuje iba ekvivalent zlomku hmotnosti na voľnom konci lana.

Skladá sa z dvoch sád kladiek: jedna, ktorá je pripevnená k podpore a druhá, ktorá vyvíja výslednú silu na záťaž. Kladky sú namontované na všeobecne kovový rám, ktorý ich drží. 

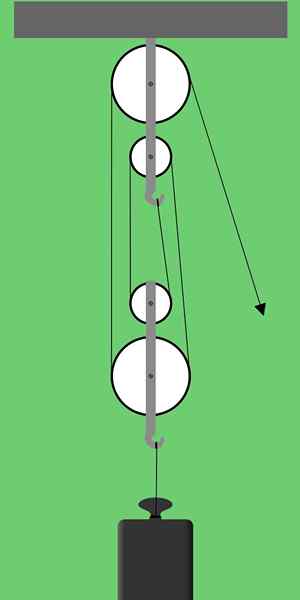
postava 1. Schéma faktoriálnej súpravy. Zdroj: Pixabay

Obrázok 1 zobrazuje faktoriálnu súpravu, ktorá pozostáva z dvoch skupín po dvoch kladkách. Tento typ usporiadaní kladky sa tiež nazýva Súpravka ani Polypasty.

[TOC]

Faktorové vzorce

Prípad 1: Mobilná kladka a pevné

Aby sme pochopili, prečo toto usporiadanie znásobuje vynakladanú silu, začneme s najjednoduchším prípadom pozostávajúcim z pevnej a mobilnej remenice.

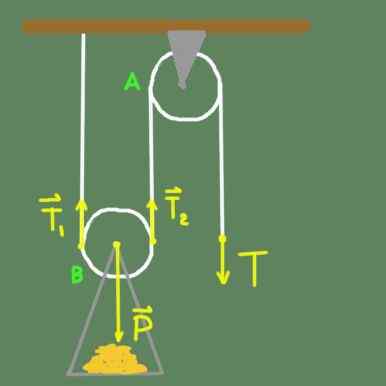Obrázok 2. Dvaja kladka.

Na obrázku 2 máme pevnú kladku na strechu pod podporou. Kladka a môže voľne otáčať okolo svojej osi. Máme tiež kladku B, ktorá má pevnú oporu na osi kladky, v ktorej je zaťaženie umiestnené. Kladka B, okrem toho, že sa môže voľne otáčať okolo svojej osi, má možnosť pohybovať sa vertikálne.

Predpokladajme, že sme v rovnovážnej situácii. Zvážte sily pôsobiace na kladku B. Os b -pulley podporuje celkovú hmotnosť p, ktorá je nasmerovaná nadol. Keby to bola jediná sila na kladku B, ale vieme, že lano, ktoré prechádza touto kladkou, tiež vyvíja dve sily, ktoré sú T1 a T2, ktoré sú nasmerované nahor.

Aby sa preložila rovnováha, musia tieto dve sily hore rovnaké ako váha, ktorá podporuje os kladky B.

T1 + T2 = P

Ale pretože kladka B je tiež v rotačnej rovnováhe, potom T1 = T2. Sily T1 a T2 pochádzajú z napätia naneseného na lano, ktoré sa nazýva T.

Môže vám slúžiť: Bohr atómový model

Preto t1 = t2 = t. Výmena v predchádzajúcej rovnici zostáva:

T + t = p

2T = P

Naznačujúc, že ​​napätie aplikované na lano je len polovica hmotnosti:

T = p/2

Napríklad, ak by zaťaženie bolo 100 kg, stačilo by na voľný koniec lana použiť silu 50 kg na zvýšenie zaťaženia pri konštantnej rýchlosti.

Prípad 2: Dva mobilné a dve pevné remenice

Zvážme napätie a sily, ktoré konajú na súbore, ktorá pozostáva z dvoch podpory podpory A a B s dvoma kladkami, každá.

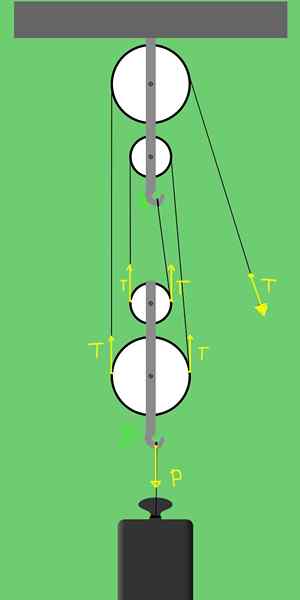Obrázok 3. Sily na plošine 2 pevných kladiek a 2 mobilných remeníc.

Podpora B má možnosť pohybovať sa vertikálne a sily pôsobiace na syna:

- Hmotnosť P záťaže, ktorá vertikálne smeruje dole.

- Dve napätia na veľkej kladke a dve napätia na malej kladke. Celkovo štyri napätie, všetky smerujú hore.

Aby existovala translačná rovnováha, je potrebné, aby sily, ktoré sa bodujú vertikálne smerom nahor, sa rovnajú zaťaženiu, ktoré smeruje nadol. To znamená, že sa musí splniť:

T + t + t + t = p

To znamená, 4 t = p

Z miesta, kde z toho vyplýva, že aplikovaná sila T na voľnom konci lana je len štvrtina hmotnosti v dôsledku záťaže, ktorá chce stúpať., T = p / 4.

S touto hodnotou pre T napätie môže byť zaťaženie udržiavané statické alebo stúpajúce s konštantnou rýchlosťou. Ak sa použilo väčšie napätie ako táto hodnota, zaťaženie by sa zrýchlilo, stav, ktorý je potrebný na jeho odstránenie z zvyšku.

Všeobecný prípad: n mobilné remenice a n pevné remenice

Ako je vidieť v predchádzajúcich prípadoch, pre každú kladku mobilnej súpravy je niekoľko síl nahor pri lane, ktoré prechádza cez kladku. Ale táto sila nemôže byť nič iné ako napätie aplikované na lano na voľnom konci.

Takže pre každú mobilnú kladku bude k dispozícii. Ale keďže v mobilnej sade sú n kladky, potom je potrebné zdôrazniť vertikálne smerom nahor je:

Môže vám slúžiť: veveričkový klietkový motor

2 n t

Pre vertikálnu rovnováhu je potrebné, aby:

2 n t = p

Preto sila aplikovaná na voľnom konci je:

T = p / (2 n)

V takom prípade je možné povedať, že sila, ktorá sa vyvíja, sa na záťaž vynásobí 2 n krát.

Napríklad, ak by sme mali faktoriálnu súpravu 3 pevných kladiek a 3 mobilov, číslo n by sa rovná 3. Na druhej strane, ak by zaťaženie bolo p = 120 kg, potom by sila aplikovaná na voľnom konci bola t = 120 kg / (2*3) = 20 kg.

Vyriešené cvičenia

Cvičenie 1

Zvážte faktoriálnu súpravu zloženú z dvoch pevných remeníc a dvoch mobilných remeníc. Maximálne napätie, ktoré môže lano podporovať, je 60 kg. Určiť, aké je maximálne zaťaženie, ktoré je možné umiestniť.

Riešenie

Keď je zaťaženie v pokoji alebo sa neustále pohybuje s jeho hmotnosťou, súvisí s napätím T v lane pomocou nasledujúceho vzťahu:

P = 2 n t

Pretože ide o súpravu dvoch mobilných a dvoch pevných kladiek, potom n = 2.

Maximálne zaťaženie, ktoré sa dá umiestniť, sa získa, keď T má maximálnu možnú hodnotu, ktorá je v tomto prípade 60 kg.

Maximálne zaťaženie = 2*2*60 kg = 240 kg

Cvičenie 2

Nájdite vzťah medzi napätím lana a hmotnosťou zaťaženia, v faktoriálnej súprave dvoch kladiek, v ktorom sa zaťaženie zrýchľuje zrýchlením do.

Riešenie

Rozdiel v tomto príklade s ohľadom na to, čo sa doteraz videlo. Navrhujeme teda Newtonov druhý zákon na nájdenie požadovaného vzťahu.

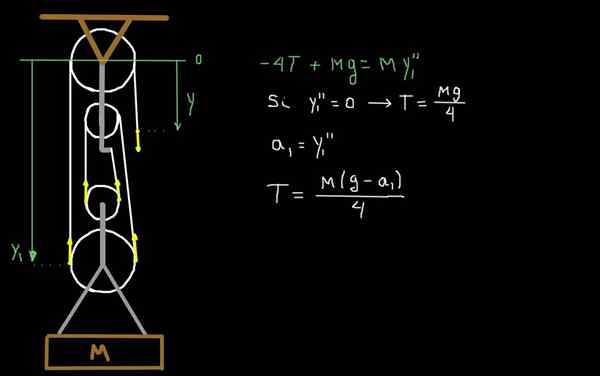Obrázok 4. Dynamika faktoriálnej súpravy.

Na obrázku 4 nakreslíme sily v dôsledku napätia t lana. Mobilná časť súpravy má celkovú hmotnosť m. Berieme ako referenčný systém jeden na úrovni prvej pevnej a pozitívnej kladky dole.

Y1 je najnižšia poloha osi kladky.

Na určenie A1 zrýchlenia mobilnej časti súpravy uplatňujeme Newtonov druhý zákon:

Môže vám slúžiť: Varignonova veta

-4 t + mg = m a1

Pretože hmotnosť záťaže je p = mg, kde g je zrýchlenie gravitácie, je možné napísať predchádzajúci vzťah:

-4T + p = P (A1 / G)

Ak by sme chceli určiť napätie aplikované v lane, keď sa určité hmotnostné zaťaženie zrýchli pomocou zrýchlenia A1, potom by bol predchádzajúci vzťah taký:

T = p (1 - a1 / g) / 4

Všimnite si, že ak bol systém v pokoji alebo sa pohyboval neustále, potom A1 = 0 a získali sme rovnaký výraz, aký sme získali v prípade 2.

Cvičenie 3

V tomto príklade sa používa rovnaká súprava cvičenia 1 s rovnakým lanom, ktoré podporuje maximálne 60 kg napätia. Určité zaťaženie stúpa a zrýchľuje ho z odpočinku na 1 m/s o 0,5 s pomocou maximálneho napätia lana. Nájdite maximálnu hmotnosť zaťaženia.

Riešenie

Použijeme výrazy získané v cvičení 2 a referenčný systém na obrázku 4, v ktorom je kladná adresa vertikálna dole.

Zrýchlenie zaťaženia je A1 = (-1 m/s -0 m/s) /0,5 s = -2 m/s^2.

Hmotnosť záťaže v kilogramovej sile je daná

P = 4 t / (1 - a1 / g)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

Toto je maximálna možná hmotnosť zaťaženia bez toho, aby sa lano zlomilo. Všimnite si, že získaná hodnota je menšia ako hodnota získaná v príklade 1, v ktorom sa zaťaženie predpokladalo s nulovým zrýchlením, to znamená v pokoji alebo konštantnej rýchlosti.

Odkazy

1. Sears, Zemansky. 2016. Fyzika univerzity s modernou fyzikou. 14. Edimatizovať. Zväzok 1. 101-120.
2. Resnick, r. (1999). Fyzický. Zvuk. 1. 3 ra ed. v španielčine. Kontinentálna redakčná spoločnosť s.Do. c.Vložka. 87-103.
3. Giancoli, D. 2006. Fyzika: Princípy s aplikáciami. 6. Edimatizovať. Sála. 72 - 96.
4. Hewitt, Paul. 2012. Koncepčná fyzická veda. 5. Edimatizovať. Pearson.38-61.
5. Serway, r., Jewett, J. (2008). Fyzika pre vedu a inžinierstvo. Zväzok 1. 7. Edimatizovať. Učenie sa. 100 - 119.