Fyzický

Zrýchlenie gravitácie, čo to je, ako sa meria a cvičí

Zrýchlenie gravitácie, čo to je, ako sa meria a cvičí

Ten Zrýchlenie gravitácie o Gravitačné zrýchlenie je definované ako intenzita pozemného gravitačného poľa. To znamená, že sila, ktorá to vyvíja na akýkoľvek objekt na jednotku hmotnosti.

Je označený už tak známym písmenom G a jeho približnou hodnotou v blízkosti zemského povrchu je 9.8 m/s2. Táto hodnota môže zažiť malé variácie s geografickou zemepisnou šírkou a tiež s výškou vzhľadom na hladinu mora.

Astronaut vo vesmíre paseo na povrchu Zeme. Zdroj: Pixabay

Zrýchlenie gravitácie, okrem toho, že má uvedenú veľkosť, má smer a význam. V skutočnosti sa smeruje vertikálne smerom do stredu Zeme.

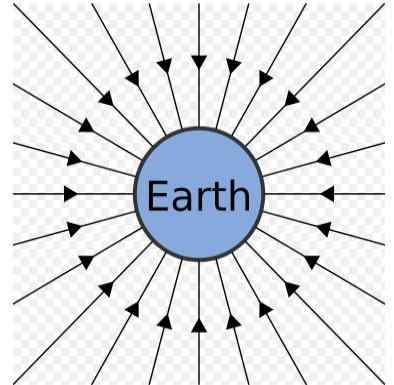Gravitačné pole Zeme. Zdroj: Zdroj: SjLegg [verejná doména]

Gravitačné pole Zeme môže byť reprezentované ako sada radiálnych čiar, ktoré ukazujú do stredu, ako je vidieť na predchádzajúcom obrázku.

[TOC]

Aké je zrýchlenie gravitácie?

Hodnota zrýchlenia gravitácie na Zemi alebo na akejkoľvek inej planéte je rovnocenná s intenzitou gravitačného poľa, ktoré vytvára, čo nezávisí od objektov, ktoré sú okolo neho, ale iba od jeho vlastnej hmoty a jeho polomeru.

Zrýchlenie gravitácie je často často definované ako zrýchlenie, ktoré zažíva akýkoľvek objekt vo voľnom páde v blízkosti zemského povrchu.

V praxi to je to, čo sa takmer vždy stáva, ako uvidíme v nasledujúcich častiach, v ktorých sa použije Newtonov univerzálny zákon o gravitačnej gravitácii.

Hovorí sa, že Newton objavil tento slávny zákon, zatiaľ čo meditoval na páde tiel pod stromom. Keď cítil ranu jablka v hlave, okamžite vedel, že sila, ktorá spôsobuje, že jablko padá, je rovnaká, čo robí mesiac obžalou okolo Zeme okolo Zeme.

Univerzálny zákon o gravitácii

Určitá alebo nie legenda o jablkach, Newton si uvedomila, že veľkosť gravitačnej príťažlivej sily medzi akýmikoľvek dvoma objektmi, napríklad medzi Zemou a Mesiacom alebo Zemou a jablkom, sa musela závisieť od ich hmotností:

Kde m1 Môže to byť hmotnosť zeme a m2, Hmotnosť mesiaca alebo jablko. Medzi telami existuje väčšia hmotnosť, väčšia príťažlivosť. Ale vo väčšej vzdialenosti, menšia sila, pretože to musí byť nepriamo úmerné štvorcovi vzdialenosti r to ich oddeľuje:

Môže vám slúžiť: elastické otrasy: v rozmere, špeciálne prípady, cvičenia

To platí bez ohľadu na to, aké veľké alebo malé sú príslušné masy. Kombináciou týchto skutočností by gravitačná sila zostala týmto spôsobom:

Na to, aby bol tento empirický zákon pripravený konštantný proporcionalita. Newton vypočítal konštantu G, takže vzorec opisuje so všetkou presnosťou pohyby nebeských telies na stupnici slnečnej sústavy a ďalej:

Kde g = 6.67 x 10-jedenásť N.m2/kg2

Charakteristiky gravitačnej sily

Gravitačná sila je vždy atraktívna; to znamená, že dve telá, na ktoré ovplyvňuje. Opak nie je možný, pretože obežné dráhy nebeských telies sú zatvorené alebo otvorené (napríklad kométy) a odpudzovacia sila nemôže nikdy produkovať uzavretú obežnú dráhu. Potom masy vždy priťahujú, nech sa stane čokoľvek.

Pomerne dobrý prístup k skutočnému tvaru Zeme (m1) A mesiac alebo jablko (m2) je predpokladať, že majú sférický tvar. Nasledujúce číslo je znázornením tohto javu.

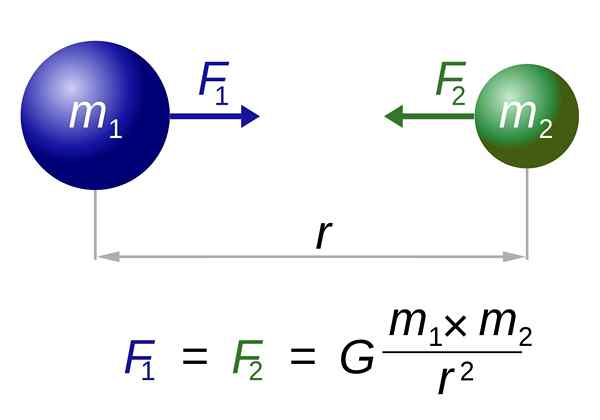Newtonov zákon o univerzálnom gravitácii. Zdroj: I, Dennis Nilsson [CC BY 3.0 (https: // creativeCommons.Org/licencie/o/3.0)]

Tu sú obidve sily vyplatené m1 O m2, Ako ten, ktorý cvičí m2 O m1, obidve rovnaké a nasmerované pozdĺž línie, ktorá sa spája s centrami. Nie sú zrušené, pretože sa uplatňujú na rôzne objekty.

Vo všetkých nasledujúcich častiach sa predpokladá, že objekty sú homogénne a sférické, a preto sa jeho ťažisko zhoduje s geometrickým centrom. Všetky koncentrované hmoty sa dajú predpokladať práve tam.

Ako sa meria gravitácia na rôznych planétach?

Gravitácia je možné merať pomocou liekov, prístroja, ktorý slúži na vykonanie závažnosti meranej v geofyzikálnom gravimetrických prieskumoch. V súčasnosti sú oveľa sofistikovanejšie ako originály, ale na začiatku boli založené na kyvadle.

Kyvadlo pozostáva z tenkého, ľahkého a nedotknuteľného lana dĺžky l. Jeden z jeho koncov je pripevnený k jednej podpore a druhý visí hmotnosť m.

Keď je systém v rovnováhe, cesto visí vertikálne, ale keď je od neho oddelené, začne sa oscilovať. Gravitácia je za to zodpovedná. Pre všetko, čo nasleduje, je platné predpokladať, že gravitácia je jedinou silou, ktorá pôsobí na kyvadlo.

Môže vám slúžiť: Aerostatický balón: História, vlastnosti, časti, ako to funguje

Obdobie hojdačky kyvadla pre malé oscilácie je dané nasledujúcou rovnicou:

Sila t nezávisí od hmotnosti, ale od dĺžky L a hodnoty g. Štvorcový členovia rovnice sú:

Vzťah medzi Tón2 a L Je lineárna: riadok formulára y = a.X, kde hodnota do, Sklon čiary je presne (4π2/g).

Experimentovať na určenie hodnoty g

Materiál

- 1 kovová sféra.

- Lano niekoľkých rôznych dĺžok, najmenej 5.

- Meracia páska.

- Dopravník.

- Chronometer.

- Podpora na nastavenie kyvadla.

- Milimeteringový papier alebo počítačový program s tabuľkou.

Postup

  1. Vyberte jeden zo strún a zostavte kyvadlo. Zmerajte dĺžku lana + polomer gule. Toto bude dĺžka l.
  2. Odstráňte kyvadlo z rovnovážnej polohy asi 5 stupňov (Id it s transportérom) a nechajte ho oscilované.
  3. Súčasne spustite stopky a zmerajte čas 10 kmitov. Zapíšte výsledok.
  4. Opakujte predchádzajúci postup pre ostatné dĺžky.
  5. Nájdite čas, ktorý vyžaduje kyvadlo na vykonanie oscilácie (vydelenie každého z predchádzajúcich výsledkov o 10).
  6. Štvorcová každá získaná hodnota, získanie T2
  7. V milimetrovom papieri graph každá hodnota T2 Na vertikálnej osi proti príslušnej hodnote L na horizontálnej osi. Buďte v súlade s jednotkami a nezabudnite vziať do úvahy chybu ocenenia použitých nástrojov: Metrická páska a stopky.
  8. Nakreslite najlepšiu čiaru, ktorá vyhovuje grafickým bodom.
  9. Nájdite svah m z tejto línie pomocou dvoch bodov, ktoré k nemu patria (nie nevyhnutne experimentálne body). Pridajte experimentálnu chybu.
  10. Vyššie uvedené kroky je možné vykonať pomocou tabuľky a možnosťou zostaviť a upraviť priamu čiaru.
  11. Z hodnoty svahu do vyčistiť hodnotu g S ich experimentálnou neistotou.

Štandardná hodnota g Na zemi, na Mesiaci a na Marse

Štandardná hodnota gravitácie na Zemi je: 9.81 m/s2, pri 45 severnej zemepisnej šírke a na hladine mora. Pretože Zem nie je dokonalá sféra, hodnoty g Mierne sa líšia a sú väčšie v póloch a maloletých v Ekvádore.

Tí, ktorí chcú poznať hodnotu v ich lokalite, ju môžu nájsť na webovej stránke Metrolhology Institute of Nemecko PTB (Fyzikalisch-technische bundesanstalt) v sekcii Informačný systém (Krieda).

Môže vám slúžiť: režisér Vektor: rovná rovnica, vyriešené cvičenia

Gravitácia na Mesiaci

Gravitačné pole Mesiaca bolo stanovené analýzou rádiových signálov vesmírnych sond obiehajúcich satelit. Jeho hodnota na lunárnom povrchu je 1.62 m/s2

Závažnosť v Marse

Hodnota gP Pre planétu závisí od jej hmotnosti M a jej polomerom nasledovne:

Preto:

Pre planétu Mars sú k dispozícii tieto údaje:

M = 6 4185 x 1023 kg

R = 3390 km

G = 6.67 x 10-jedenásť N.m2/kg2

S týmito údajmi vieme, že závažnosť Mars je 3.71 m/s2. Rovnaká rovnica sa prirodzene môže uplatniť na údaje o mesiaci alebo na akúkoľvek inú planétu, a tak odhadnúť hodnotu jej závažnosti.

Vyriešené cvičenie: jablko, ktoré padá

Predpokladajme, že Zem aj jablko majú sférický tvar. Hmotnosť Zeme je m = 5,98 x 1024 kg a jeho polomer je r = 6,37 x 106  m. Hmotnosť jablka je m = 0.10 kg. Predpokladajme, že neexistuje iná sila okrem gravitácie. Z Newtonovho zákona o univerzálnom gravitácii:

a) gravitačná sila vyvíjaná na jablko.

b) Zrýchlenie, ktoré zažíva Apple pri jeho uvoľňovaní z určitej výšky, podľa druhého zákona Newtona.

Riešenie

a) Jablko (predpokladané sférické, rovnako ako Zem) má veľmi malý polomer v porovnaní s pozemským polomerom a je ponorené do svojho gravitačného poľa. Nasledujúce číslo nie je evidentne, ale existuje schéma gravitačného poľa g, a Strengh F Cvičené Zemou na jablku:

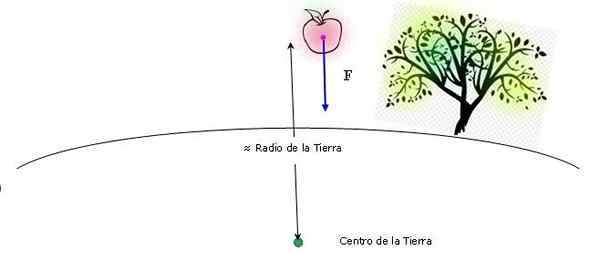Schéma, ktorá ukazuje pád jablka v blízkosti Zeme. Veľkosť jablka a výška pádu sú opovrhnutiahodné. Zdroj: Self Made.

Pri uplatňovaní Newtonovho zákona o univerzálnom gravitácii sa vzdialenosť medzi centrami môže považovať za približne rovnakú hodnotu ako polomer Zeme (výška, z ktorej je jablko padá, zanedbateľná v porovnaní s pozemským polomerom). Preto:

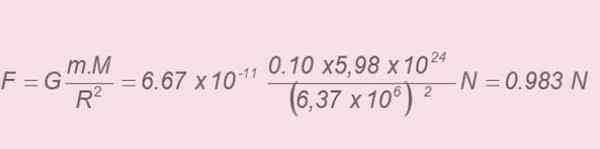
b) Podľa Newtonovho druhého zákona je veľkosť sily vyvíjanej na jablko:

F = ma = mg

Ktorého hodnota je 0.983 n, podľa predchádzajúceho výpočtu. Vyrovnanie obidvoch hodnôt a potom sa získa vyčistenie veľkosti zrýchlenia:

mg = 0.983 n

G = 0.983 N/0.10 kg = 9.83 m/s2

Toto je veľmi dobrý prístup k štandardnej hodnote gravitácie.

Odkazy

  1. Giancoli, D. (2006). Fyzika: Princípy s aplikáciami. Šieste vydanie. Sála. 118-122.
  2. Hewitt, Paul. (2012). Koncepčná fyzická veda. Piaty vydanie. Pearson. 91 - 94.
  3. Rex, a. (2011). Základy fyziky. Pearson. 213-221.