Rôznostranný trojuholník

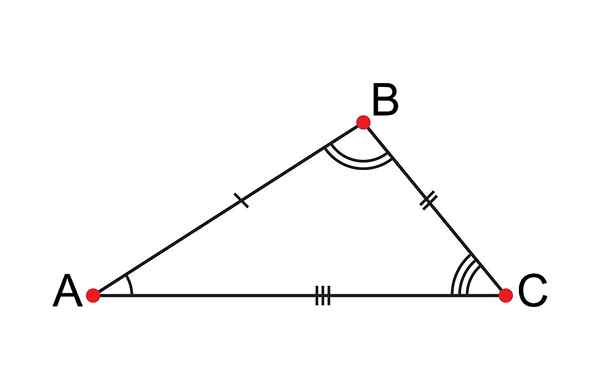
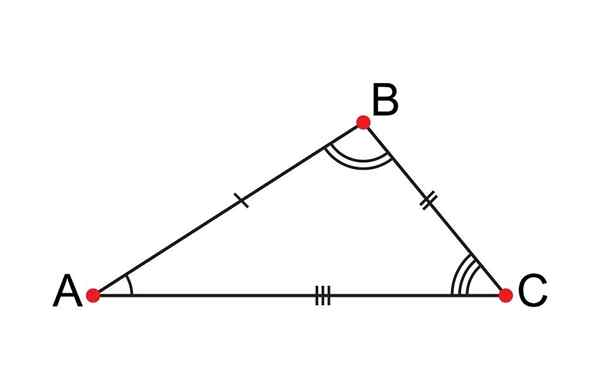Scalen trojuholník má všetky svoje nerovnaké strany

Čo je to Scalene Triangle?

A Rôznostranný trojuholník Je to tromi polygón, kde má každý rôzne opatrenia alebo dĺžky; Z tohto dôvodu dostal meno Escaleno, čo v latinčine znamená nerovnaké.

Trojuholníky sú polygóny považované za najjednoduchšie v geometrii, pretože sa tvoria tri strany, tri uhly a tri vrcholy. V prípade Scalenovho trojuholníka, pretože má všetky rôzne strany, naznačuje, že jeho tri uhly budú tiež.

Charakteristiky mierky trojuholníkov

Mierky sú jednoduché polygóny, pretože žiadna z jeho strán alebo uhlov nemá rovnaké opatrenie, na rozdiel od izoscelov a rovnovážnych trojuholníkov.

Pretože všetky ich strany a uhly majú rôzne opatrenia, tieto trojuholníky sa považujú za nepravidelné konvexné polygóny.

Podľa amplitúdy vnútorných uhlov sa ScaleNy trojuholníky klasifikujú ako:

• Trojuholník: Všetky jeho strany sú rôzne. Jeden z jeho uhlov je rovný (90^ani) a ostatné sú akútne a s rôznymi opatreniami.
• Tupá trojuholník: Všetky jeho strany sú rôzne a jeden z jeho uhlov je tupý (> 90^ani).
• Scalen Acutangle trojuholník: Všetky jeho strany sú rôzne. Všetky jeho uhly sú akútne (< 90^ani) S rôznymi opatreniami.

Ďalšou charakteristikou trojuholníkov Scale.

Komponenty/prvky

Stredný

Je to čiara, ktorá odchádza zo stredu na jednej strane a dosahuje opačný vrchol. Tri médiá sa zúčastňujú v bode zvanom Baricentro alebo Centroid.

Bisektor

Je to čiastočne, ktorý rozdeľuje každý uhol do dvoch uhlov rovnakej miery. Bisektory trojuholníka sa zhodujú v bode nazývané stimul.

Mediacia

Je to segment kolmá na stranu trojuholníka, ktorý pochádza v strede tohto. V trojuholníku sú tri mediácie a zúčastňujú.

Výška 

Je to čiara, ktorá prechádza zo vrcholu na opačnú stranu, a tiež táto čiara je kolmá na túto stranu. Všetky trojuholníky majú tri výšky, ktoré sa zhodujú v bode nazývanom ortotenter.

Vlastnosti Escaleno Triange

Mierky sú definované alebo identifikované, pretože majú niekoľko vlastností, ktoré ich zastupujú, pochádzajú z teorémov navrhnutých veľkými matematikmi. Oni sú:

Vnútorné uhly

Súčet vnútorných uhlov sa vždy rovná 180^ani.

Súčet strán

Súčet opatrení dvoch strán by mal byť vždy väčší ako miera tretej strany, a + b> c.

Nezmyselné strany

Všetky strany horolezeckých trojuholníkov majú rôzne opatrenia alebo dĺžky; to znamená, že sú nezmyselné.

Nezmyselné uhly

Pretože všetky strany Scalenovho trojuholníka sú rôzne, jeho uhly budú tiež. Súčet vnútorných uhlov sa však bude vždy rovnať 180 ° av niektorých prípadoch môže byť jeden z jeho uhlov tupá alebo rovná, zatiaľ čo v iných budú všetky jeho uhly akútne.

Môže vám slúžiť: multiplikačné problémy pre deti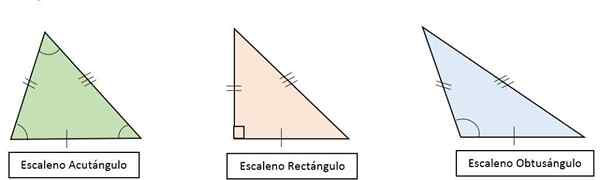 Typy trojuholníkov Scale podľa ich uhlov

Výška, medián, mediatrix a bisektor nie sú náhodné

Rovnako ako každý trojuholník, aj Escaleno má rôzne riadky riadkov, ktoré ho tvoria, ako napríklad: výška, stredná, Mediatrix a Bisector.

Kvôli osobitosti svojich strán sa v tomto type trojuholníka žiadna z týchto línií nezhoduje v jednom.

Orocentro, Baricentro, Incentro a CirundCentro nie sú náhodné

Rovnako ako výška, medián, bisektor a Mediatrix sú reprezentované rôznymi segmentmi línií, v Scalenom trojuholníku sa nachádzajú body stretnutia -ortocenter, incentrum a obvody Baricenter sa nachádzajú v rôznych bodoch (to znamená, že sa nezhodujú).

V závislosti od toho, či je trojuholník akcutangle, obdĺžnik alebo tupý, má ortocenter rôzne miesta:

do. Ak je trojuholník acutangle, ortocenter bude vo vnútri trojuholníka.

b. Ak je trojuholník obdĺžnik, ortocenter sa zhoduje s vrcholom na priamej strane.

c. Ak je trojuholník tupý, ootocenter bude mimo trojuholníka.

Relatívna výška

Výšky sú relatívne k stranám.

V prípade Scalenovho trojuholníka bude mať tieto výšky rôzne opatrenia. Každý trojuholník má tri relatívne výšky a na ich výpočet sa používa Herón.

Výpočet obvodu, plocha, výška a boky

Ako vypočítať obvod?

Obvod polygónu sa vypočíta na základe súčtu strán.

Rovnako ako v tomto prípade má Scalen Triangle všetky svoje strany s iným opatrením, jeho obvod bude:

P = strana až + strana B + strana C.

Ako vypočítať oblasť?

Trojuholníky sa vždy vypočítavajú s rovnakým vzorcom, ktoré vynásobia základňu podľa výšky a delia sa dvoma:

Oblasť = (základňa _* H) ÷ 2

V niektorých prípadoch nie je známa výška trojuholníka Scalen, ale existuje receptúra, ktorú navrhol matematik Herón, na výpočet oblasti, ktorá pozná mieru troch strán trojuholníka.

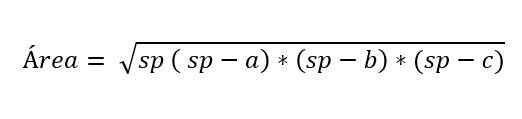
Kde:

• A, B a C predstavujú strany trojuholníka.
• SP zodpovedá semi -erimetra trojuholníka, to znamená polovicu obvodu:

sp = (a + b + c) ÷ 2

V prípade, že sa uplatnili iba dve strany trojuholníka a uhol, ktorý sa vytvára medzi nimi, oblasť je možné vypočítať uplatňovaním trigonometrických dôvodov. Preto musíte:

Oblasť = (strana _* H) ÷ 2

Kde výška (h) je produkt na jednej strane cez opačný uhol. Napríklad pre každú stranu bude oblasť:

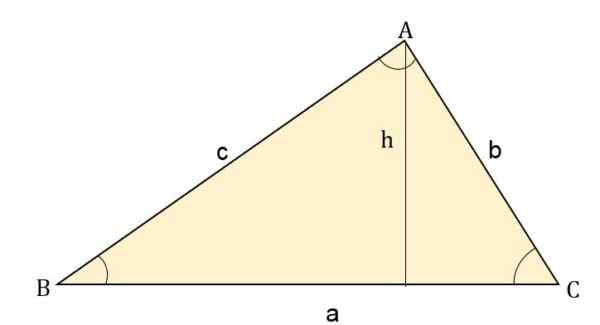
• Oblasť = (b _* c _* hriech a) ÷ 2
• Oblasť = (a _* c _* hriech B) ÷ 2.
• Oblasť = (a _* b _* Sen C) ÷ 2

Ako vypočítať výšku?

Rovnako ako všetky strany Scalenovho trojuholníka, aj keď sú rôzne, nie je možné vypočítať výšku pomocou vety Pythagory.

Z herónovej receptúry, ktorá je založená na opatreniach troch strán trojuholníka, je možné vypočítať oblasť.

Môže vám slúžiť: faktorové notácie: Koncept, príklady a cvičenia

Výška môže byť zrejmá od všeobecného vzorca oblasti:

Vzorec na výpočet výšky Scalenovho trojuholníka

Strana je nahradená meradlom strany A, B alebo C.

Ďalším spôsobom, ako vypočítať výšku, keď je známa hodnota jedného z uhlov, je uplatňovanie trigonometrických dôvodov, kde výška bude predstavovať trojuholníkový kateto.

Napríklad, keď je známy opačný uhol výške, bude určený prsníkmi:

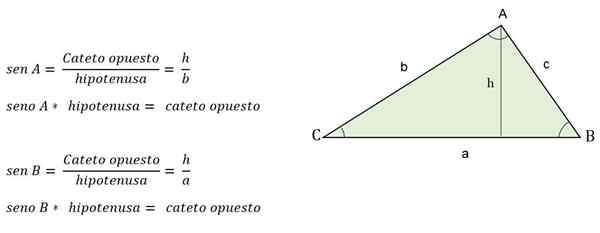Trigonometrický vzorec na výpočet výšky Scalenového trojuholníka

Ako vypočítať strany?

Ak máte mieru dvoch strán a uhla na rozdiel od nich, je možné určiť tretiu stranu a aplikovať Cosenosovu vetu.

Napríklad v trojuholníku AB sa nakreslí výška v porovnaní so segmentom striedavého prúdu. Týmto spôsobom je trojuholník rozdelený na dva trojuholníky obdĺžnika.

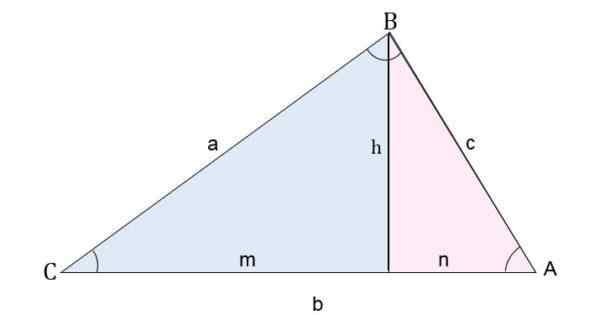Rozdelenie Scalenovho trojuholníka do dvoch obdĺžnikov na výpočet bokov

Na výpočet strany C (segment AB) sa aplikuje veta Pythagoras pre každý trojuholník:

• Pre modrý trojuholník musíte:

c² = h² + m²

Ako m = b - n, vymení sa:

c² = h² + b² (B - n)²

c² = h² + b² - 2Bn + N².

• Pre ružový trojuholník musíte:

h² = a² - n²

Nahradí sa v predchádzajúcej rovnici:

c² = a² - n² + b² - 2Bn + N²

c² = a² + b² - 2 miliárd.

Vedieť, že n = a _* cos c, je nahradený v predchádzajúcej rovnici a získa sa hodnota strany C:

c² = a² + b² - 2B_* do _* cos c.

Podľa zákona Cosenos je možné strany vypočítať ako:

• do² = b² + c² - 2B_* c _* tma.
• b² = a² + c² - Druhý_* c _* cos B.
• c² = a² + b² - 2B_* do _* cos c.

Existujú prípady, keď nie sú známe miery trojuholníkových strán, ale jeho výška a uhly, ktoré sa tvoria vo vrcholoch. Na určenie oblasti v týchto prípadoch je potrebné uplatniť trigonometrické dôvody.

Poznanie uhol jedného z jeho vrcholov je identifikovaná kategória a používa sa zodpovedajúci trigonometrický dôvod:

Trigonometrický vzorec na výpočet bokov Scalen Triangle

Napríklad Cateto AB bude opačný pre uhol C, ale v susedstve uhlu a. V závislosti od strany alebo nohy zodpovedajúcej výške sa druhá strana vymaže, aby sa získala hodnota tohto.

Vyriešené cvičenia

Prvé cvičenie

Vypočítajte plochu a výšku trojuholníka Escalano ABC s vedomím, že jeho strany sú:

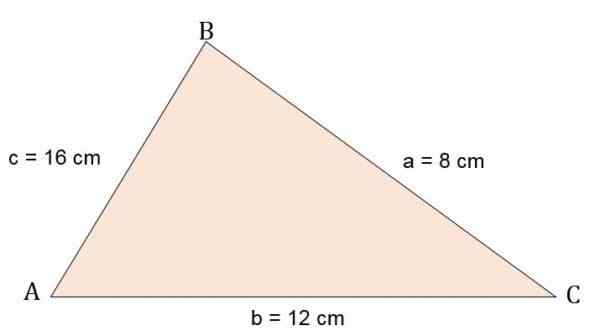
A = 8 cm.

B = 12 cm.

C = 16 cm.

Riešenie

Pretože údaje sú uvedené opatrenia troch strán Scalen Triangle.

Pretože nemáte hodnotu výšky, oblasť je možné určiť použitím vzorec Herón.

Najprv sa vypočíta poloperimeter:

sp = (a + b + c) ÷ 2

sp = (8 cm + 12 cm + 16 cm) ÷ 2

sp = 36 cm ÷ 2

sp = 18 cm.

Teraz sú hodnoty vo vzorec Herón nahradené:

Môže vám slúžiť: Absolútna frekvencia: vzorec, výpočet, distribúcia, príklad Herón

Poznanie oblasti je možné vypočítať relatívnu výšku s bokom b. Z celkového vzorca, vyčistite ho:

Oblasť = (strana _* H) ÷ 2

46, 47 cm² = (12 cm _* H) ÷ 2

H = (2 _* 46,47 cm²) ÷ 12 cm

H = 92,94 cm² ÷ 12 cm

H = 7,75 cm.

Druhé cvičenie

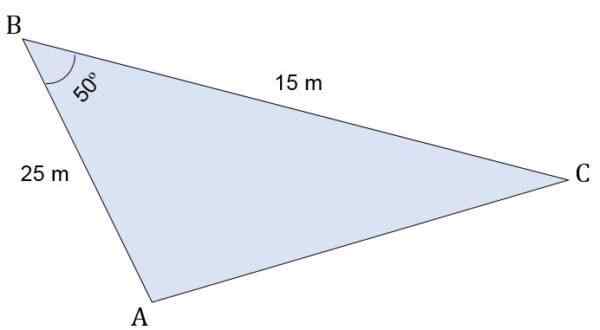
Vzhľadom na trojuholník ABC Escalano, ktorého opatrenia sú:

• Segment AB = 25 m.
• Segment BC = 15 m.

Vo vrchole B sa vytvorí uhol 50 °. Vypočítajte výšku vzhľadom na stranu C, obvod a plochu tohto trojuholníka.

Riešenie

V takom prípade existujú dve opatrenia. Na určenie výšky je potrebné vypočítať mieru tretej strany.

Pretože opačný uhol je daný danými stranami, je možné uplatniť zákon Cosenos na určenie miery strany AC (B):

b² = a² + c² - Druhý_*c _* cos B

Kde:

A = BC = 15 m.

C = AB = 25 m.

B = ac.

B = 50^ani.

Údaje sa nahradia:

b² = (15)² + (25)² - 2_*(pätnásť)_*(25) _* cos 50

b² = (225) + (625) - (750) _* 0,6427

b² = (225) + (625) - (482 025)

b² = 367 985

B = √367 985

B = 19,18 m.

Keďže už máte hodnotu troch strán, vypočíta sa obvod tohto trojuholníka:

P = strana až + strana B + strana C

P = 15 m + 25 m + 19, 18 m

P = 59,18 m

Teraz je možné určiť oblasť uplatňovaním vzorec Herón, ale najprv sa musí vypočítať poloperimeter:

sp = p ÷ 2

sp = 59,18 m ÷ 2

sp = 29,59 m.

Opatrenia strán a poloperimeter vo vzorec Herón sú nahradené:

Nakoniec, keď poznáte oblasť, relatívna výška sa dá vypočítať na stranu C. Z celkového vzorca, vyčistite ho, musíte:

Oblasť = (strana _* H) ÷ 2

143,63 m² = (25 m _* H) ÷ 2

H = (2 _* 143,63 m²) ÷ 25 m

H = 287,3 m² ÷ 25 m

H = 11,5 m.

Tretie cvičenie

V trojuholníku Escaleno ABC meria strana B, strana C meria 22 cm a vo vrchole A je uhol 90^ani. Vypočítajte oblasť tohto trojuholníka.

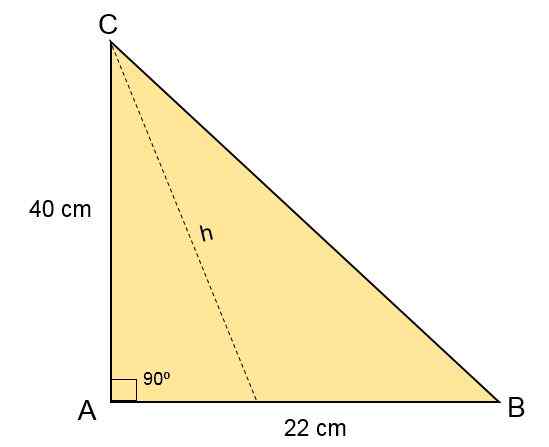
Riešenie

V tomto prípade sú uvedené miery dvoch strán trojuholníka v mierke ABC, ako aj uhol, ktorý sa tvorí vo vrchole.

Na určenie oblasti nie je potrebné vypočítať mieru strany A, pretože z trigonometrických dôvodov sa uhol používa na jej nájdenie.

Pretože opačný uhol je známy výške, bude to určený produktom na jednej strane a prsníkom uhla.

Výmena vo vzorci oblasti, ktorú musíte:

• Oblasť = (strana _* H) ÷ 2
• H = c _* hriech a

Oblasť = (b _* c _* hriech a) ÷ 2

Oblasť = (40 cm _* 22 cm _* Sen 90) ÷ 2

Oblasť = (40 cm _* 22 cm _* 1) ÷ 2

Oblasť = 880 cm² ÷ 2

Oblasť = 440 cm².

Odkazy

1. Álvaro Rendón, do. R. (2004). Technická kresba: Notebook aktivity.
2. Ángel Ruiz, h. B. (2006). Geometria. CR technologický, .
3. Anjel, a. R. (2007). Elementárna algebra. Pearson Vzdelanie,.
4. Baldor, a. (1941). Algebra. Havana: kultúra.
5. Barbosa, J. L. (2006). Plochá euklidovská geometria. Rio de Janeiro,.
6. Coxeter, h. (1971). Základy geometrie. Mexiko: Limusa-Wiley.
7. Daniel C. Alexander, G. M. (2014). Základná geometria pre študentov vysokých škôl. Učenie sa.
8. Harpe, P. d. (2000). Témy v teórii geometrických skupín. University of Chicago Press.